Ответы. Задача по теме Работа. Мощность. Ответы
 Скачать 1.58 Mb. Скачать 1.58 Mb.
|
|
БИЛЕТ №27 1)Поступательное, вращательное и плоское движения твердых тел. 2)Полная механическая энергия. Закон изменения полной механической энергии. 3)Задача по теме «Момент инерции». Ответы: 1) ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА В твердом теле скорости точек распределяются таким образом, что проекции скоростей двух точек на прямую, их соединяющую, равны между собой (кинематическое определение твердого тела). Положение твердого тела в общем случае определяется шестью параметрами; в частных случаях, когда на движение тела наложены ограничения, число параметров соответственно уменьшается. Поступательным движением твердого тела называется такое его движение, при котором всякая прямая, неизменно связанная с телом, перемещается параллельно самой себе. Для этого достаточно, чтобы две непараллельные прямые, связанные с телом, перемещались параллельно самим себе. При поступательном движении все точки тела описывают одинаковые, параллельно расположенные траектории и имеют в любой момент времени одинаковые скорости и ускорения. Таким образом, поступательное движение тела определяется движением одной его точки О. Вращательным называют такое движение твердого тела, при котором две какие-нибудь точки принадлежащие телу, остаются во все время движения неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все точки лежащие на оси так же неподвижны. Чтобы определить положение вращающегося тела, введем две плоскости, проходящие через ось вращения (рис. 50 ) А - плоскость неподвижная; В - плоскость связанная с телом и вращающаяся с ним; DE - ось вращения, совпадающая с осью z. Теперь в любой момент времени положение тела будет определяться углом между плоскостями А и В или углом поворота тела, положительным, если вращение происходит против часовой стрелки, и отрицательным в противном случае. Закон вращательного движения Угол поворота обычно измеряют в радианах. Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость и угловое ускорение . Если за промежуток времени Угловой скоростью тела в данный момент t называется величина, к которой стремится средняя угловая скорость , если стремится к нулю. Угловая скорость твердого тела является первой производной от угла поворота по времени. Размерность: [радиан/время]; [1/время]; [1/сек =]. Угловую скорость можно изображать вектором. Вектор угловой скорости направляют по оси вращения в ту сторону, откуда вращение видно против хода часовой стрелки. Если угловая скорость не является постоянной величиной, то вводят еще одну характеристику вращения - угловое ускорение. Угловое ускорение характеризует изменение угловой скорости тела с течением времени. Если за промежуток времени Угловым ускорением твердого тела в данный момент времени t называется величина к которой стремится при стремящемся к нулю 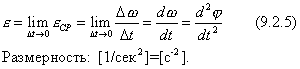 Как вектор, угловое ускорение направлен так же, как и , вдоль оси (рис. 51 ) Если направление и совпадает, то вращение ускоренное, если противоположно, то замедленное. Если = const, то вращение будет равномерным. Найдем его закон. Так как Это и есть закон равномерного вращения. В технике вращение характеризуют оборотами в минуту n [об/мин]. Угловая скорость и обороты в минуту n связаны следующим соотношением: Если угловое ускорение тела все время остается постоянным, то вращение называют равнопеременным (= const). Найдем закон вращения, если в начальный момент t = 0, = 0 и : Подставляем вместо правую часть (9.2.3), разделяем переменные и, вновь интегрируя, имеем 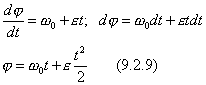 Это закон равнопеременного вращения. Если и имеют один знак, то вращение равноускоренное. Если знаки разные - равнозамедленное. (рис. 51, а,б). Плоским (плоскопараллельным) назыв. такое движение, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости.Уравнения плоского движения: xA= f1(t), yA= f2(t), j = f3(t), точка А назыв. полюсом. Плоское движение тв.тела слагается из поступательного движения, при котором все точки тела движутся так же, как полюс (А),и из вращательного движения вокруг этого полюса. Полная механическая энергия тела не изменяется. Энергия только превращается из одного вида в другой. Полная механическая энергия тела, на которое не действуют силы трения и сопротивления, в процессе его движения остается неизменной. Полной механической энергией тела называют сумму его кинетической и потенциальной энергий. Сумма кинетической и потенциальной энергий образует полную механическую энергию тела. Абсолютно упругим называется такой удар, при котором полная механическая энергия тел сохраняется. Какие причины могут изменить полную механическую энергию? Р 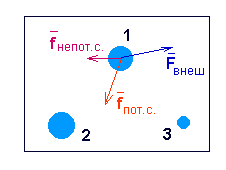 ассмотрим систему тел, в которой действуют следующие силы: ассмотрим систему тел, в которой действуют следующие силы:
Изменение кинетической энергии системы равно суммарной работе всех сил, действующих на тела этой системы (см. тему 3): DEк = Aпот.с.+ Aнепот.с.+ Aвнеш.с. (1) Изменение потенциальной энергии системы равно работе потенциальных сил с обратным знаком (см. тему 4): DEп = - Aпот.с. (2) Очевидно, что изменение полной механической энергии равно: DE = DEп + DEк (3) Из уравнений (1-3) получим, что изменение полной механической энергии равно суммарной работе всех внешних сил и внутренних непотенциальных сил. DEк = Aвнеш.с.+ Aнепот.с. (4) Формула (4) представляет из себя закон изменения полной механической энергии системы тел. Существует 2 причины изменения энергии системы:
Очевидно, что полная механическая энергия замкнутой системы, в которой действуют только потенциальные силы, не изменяется при любых перемещениях тел. Это утверждение называется законом сохранения механической энергии. БИЛЕТ№28 1)Вращательное движение. Угловая скорость. Угловое ускорение. 2)Уравнение гармонических колебаний на примере математического маятника. 3)Задача по теме «Энергия». Ответы: 1) Движение материальной точки или поступательное движение тела характеризуют в зависимости от времени линейные величины s (путь, расстояние), v (скорость) и а (ускорение) с его составляющими at и an. Вращательное движение тела в зависимости от времени t характеризуют угловые величины: φ (угол поворота в радианах), ω (угловая скорость в рад/сек) и ε (угловое ускорение в рад/сек2). Закон вращательного движения тела выражается уравнением φ = f (t). Угловая скорость – величина, характеризующая быстроту вращения тела, определяется в общем случае как производная угла поворота по времени ω = dφ/dt = f' (t). Угловое ускорение – величина, характеризующая быстроту изменения угловой скорости, определяется как производная угловой скорости ε = dω/dt = f'' (t). Приступая к решению задач на вращательное движение тела, необходимо иметь в виду, что в технических расчетах и задачах, как правило, угловое перемещение выражается не в радианах φ, а в оборотах φоб. Поэтому необходимо уметь переходить от числа оборотов к радианному измерению углового перемещения и наоборот. Так как один полный оборот соответствует 2π рад, то φ = 2πφоб и φоб = φ/(2π). Угловая скорость в технических расчетах очень часто измеряется в оборотах, произведенных в одну минуту (об/мин), поэтому необходимо отчетливо уяснить, что ω рад/сек и n об/мин выражают одно и то же понятие – скорость вращения тела (угловую скорость), но в различных единицах – в рад/сек или в об/мин. Переход от одних единиц угловой скорости к другим производится по формулам ω = πn/30 и n = 30ω/π. 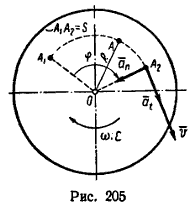 При вращательном движении тела все его точки движутся по окружностям, центры которых расположены на одной неподвижной прямой (ось вращающегося тела). Очень важно при решении задач, приведенных в этой главе, ясно представлять зависимость между угловыми величинами φ, ω и ε, характеризующими вращательное движение тела, и линейными величинами s, v, at и an, характеризующими движение различных точек этого тела (рис 205). Если R – расстояние от геометрической оси вращающегося тела до какой-либо точки А (на рис. 205 R=OA), то зависимость между φ – углом поворота тела и s – расстоянием, пройденным точкой тела за то же время, выражается так: s = φR. Зависимость между угловой скоростью тела и скоростью точки в каждый данный момент выражается равенством v = ωR. Касательное ускорение точки зависит от углового ускорения и определяется формулой at = εR. Нормальное ускорение точки зависит от угловой скорости тела и определяется зависимостью an = ω2R. При решении задачи, приведенной в этой главе, необходимо ясно понимать, что вращением называется движение твердого тела, а не точки. Отдельно взятая материальная точка не вращается, а движется по окружности – совершает криволинейное движение. 2)??????? Билет № 29 1)Сила инерции. Эквивалентность сил инерции и гравитации. Равенство гравитационной и инертной масс. Центробежная сила инерции. 2)Упругое столкновение двух частиц. Нецентральный удар. 3)Задача по теме «Кинематика». Ответы: 1) Силы инерции — силы, обусловленные ускоренным движением неинерциальной системы отсчета (НСО) относительно инерциальной системы отсчета (ИСО). Основной закон динамики для неинерциальных систем отсчета: , где — сила, действующая на тело со стороны других тел; — сила инерции, действующая на тело относительно поступательно движущейся НСО. — ускорение НСО относительно ИСО. Она появляется, например, в самолете при разгоне на взлетной полосе; — центробежная сила инерции, действующая на тело относительно вращающейся НСО. — угловая скорость НСО относительно ИСО, — расстояние от тела до центра вращения; — кориолисова сила инерции, действующая на тело, движущееся со скоростью относительно вращающейся НСО. — угловая скорость НСО относительно ИСО (вектор направлен вдоль оси вращения в соответствии с правилом правого винта). Принцип эквивалентности сил гравитации и инерции — эвристический принцип, использованный Альбертом Эйнштейном при выводе общей теории относительности. Один из вариантов его изложения: «Силы гравитационного взаимодействия пропорциональны гравитационной массе тела, силы инерции же пропорциональны инертной массе тела. Если инертная и гравитационная массы равны, то невозможно отличить, какая сила действует на данное тело — гравитационная или сила инерции.» Центробежная сила инерции - сила, с которой связь действует на материальную точку, равномерно движущуюся по окружности, в системе отсчета, связанной с этой точкой. Центробежная сила инерции приложена к движущейся материальной точке и направлена по радиусу вращения от центра. 2) Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел. Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара. При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой. Частным случаем нецентрального упругого удара может служить соударение двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров БИЛЕТ №30. 1)Нерелятивистская ракета. Формула Циолковского. 2)Полная механическая энергия. Закон сохранения механической энергии. 3)Задача по теме «Кинематика вращательного движения». О  тветы:1) тветы:1)  Формула Циолковского: Рассмотрим ускорение ракеты в прямолинейном движении, считая, что скорость выбрасываемых газов относительно постоянная. Уравнение(46.6)запишется так: Формула Циолковского: Рассмотрим ускорение ракеты в прямолинейном движении, считая, что скорость выбрасываемых газов относительно постоянная. Уравнение(46.6)запишется так: Однако это сильно завышенное значение, потому что мы не учли что часть энергии, образовавшейся при сгорании, теряется на излучение, нагревание стенок двигателя и т.д. Кроме того выбрасываемые из ракетного двигателя частицы не движутся все строго в одном направлении, а расходятся в пределах некоторого конуса. Это снижает величину достижимых значений u’. 2) Сумма кинетической и потенциальной энергий системы тел называется полной механической энергиейсистемы. E = Ep + Ek. Учитывая, что при совершении работы A = DEk и, одновременно, A = - DEp, получим: DEk = - DEp или D(Ek + Ep)=0 - изменение суммы кинетической и потенциальной энергий (т.е. изменение полной механической энергии) системы равно нулю. DEk = - DEp Значит, полная энергия системы остается постоянной: E = Ep + Ek = const. В замкнутой системе, в которой действуют только консервативные силы, механическая энергия сохраняется. (Или: полная механическая энергия системы тел, взаимодействующих силами упругости и гравитации, остается неизменной при любых взаимодействиях внутри этой системы). E = Ep + Ek = const Например, для тела, движущегося под действием силы тяжести (падение; тело, брошенное под углом к горизонту, вертикально вверх или движущееся по наклонной плоскости без трения): 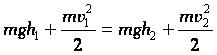 . .БИЛЕТ №31. 1)Работа силы. Механическая работа. 2)Момент импульса. Закон сохранения момента импульса. 3)Задача по теме «Кинематика поступательного движения». Ответы: РАБОТА силы - мера действия силы, зависящая от численной величины и направления силы F и от перемещения s точки ее приложения. Если сила F численно и по направлению постоянная, а перемещение прямолинейно, то работа A = F?s?cos ?, где ? - угол между направлениями силы и перемещения. “Работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии частицы“. Однако в следующем параграфе этого же учебника работа силы трактуется уже, как причина приращения потенциальной энергии, из чего можно сделать вывод, что работа сил идет на приращение любого вида энергии. Что именно понимается под видами энергии, показано на странице, посвященной формам и видам энергии. В физике "механической работой" называют работу какой-нибудь силы ( силы тяжести, упругости, трения и т.д.) над телом, в результате действия которой тело перемещается. |
