численные методы. Задача принятия решений общая постановка, примеры
 Скачать 1.64 Mb. Скачать 1.64 Mb.
|
Упражнения к § 1Основные упражненияВласти города M решают вопрос о выборе площадки для строительства аэропорта. Сформулировать возможное множество альтернатив и критерии, которыми может руководствоваться комиссия при выборе площадки для постройки. Корпорация «A&A» проводит конкурс студентов на соискание одной стипендии в рамках программы «Молодая экономика». Программа «Молодая экономика» реализуется холдингом в целях: активизации интереса студентов к решению социально-экономических проблем Воронежской области; создания в регионе условий для профессионального продвижения наиболее перспективных студентов; популяризация идеи «регионального патриотизма». Описать множество альтернатив задачи выбора корпорацией лучших студентов, сформулировать возможные критерии отбора и описать процесс решения задачи выбора. Дополнительные упражненияСтудент, имея предоставленную в № 2 основных упражнений о программе информацию, решает вопрос о выборе тематики научной работы с целью принятия участия в конкурсе. Описать критерии, которыми может руководствоваться студент при выборе тематики. Какие возможны принципы оптимальности? Повлияет ли на его выбор следующая информация: один из наиболее известных проектов, реализуемых холдингом в текущем году, – создание перерабатывающего комплекса на основе сахарного завода? Сформулировать множество альтернатив, возможные критерии выбора и принципы оптимальности для примеров 1–2. Правительство страны F решило пересмотреть макроэкономическую политику. Для этого ученые разработали экономико-математическую модель, в которой при определенных значениях управляющих переменных получается одно из возможных решений. Качество решений оценивалось по 4 критериям: С1 – увеличение валового национального продукта (в %); С2 – уменьшение инфляции (в %); С3 – уменьшение безработицы (в %); С4 – уменьшение дефицита внешней торговли (в ден. единицах). В таблице приведены полученные варианты экономической политики. В нижней строке приведены наилучшие значения каждого из критериев, которые можно получить, если взять один критерий как основной, а на другие не обращать внимания. Значения критериев оценки вариантов экономической политики
Описать принципы оптимальности, которые могут быть использованы при выборе одного из перечисленных вариантов. Какой вариант будет выбран в соответствии с построенными Вами принципами? § 2. Теоретические основы выбора альтернатив 2.1. Понятие бинарного отношения. Способы задания бинарных отношений Бинарным отношением R на множестве X произвольной природыназывается подмножество R множества 1. Перечисление всех пар элементов (x,y), которые содержатся в R. 2. Задание отношения матрицей смежности. Пусть Xсостоит из n элементов, R - бинарное отношение на X. Занумеруем элементы X целыми числами от 1 до n. Матрицей смежности бинарного отношения называется квадратная матрица 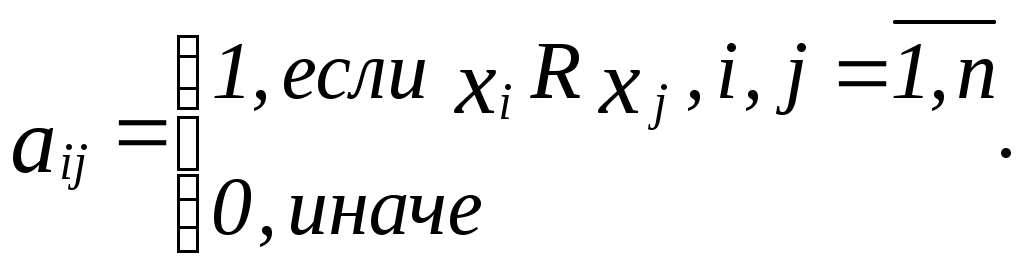 3. Задание графом. Под графом бинарного отношения понимается схема, в которой элементы множества X изображаются точками на плоскости, элементы 4. Задание сечениями. Данный способ задания бинарного отношения, в отличие от способов 1-3, пригоден для задания отношений и на бесконечных множествах. Верхним сечением элемента Аналогично определяется нижнее сечение: Отношение R полностью задано, если для каждого Отношение R называется пустым (), если оно не выполняется ни для одной пары Для справедливо: 1) Отношение R называется полным (U), если оно выполняется для всех пар Для U справедливо: 1) Отношение R называется диагональным (E), если оно выполняется для тех и только для тех пар, которые состоят из совпадающих элементов: Для E справедливо: 1) 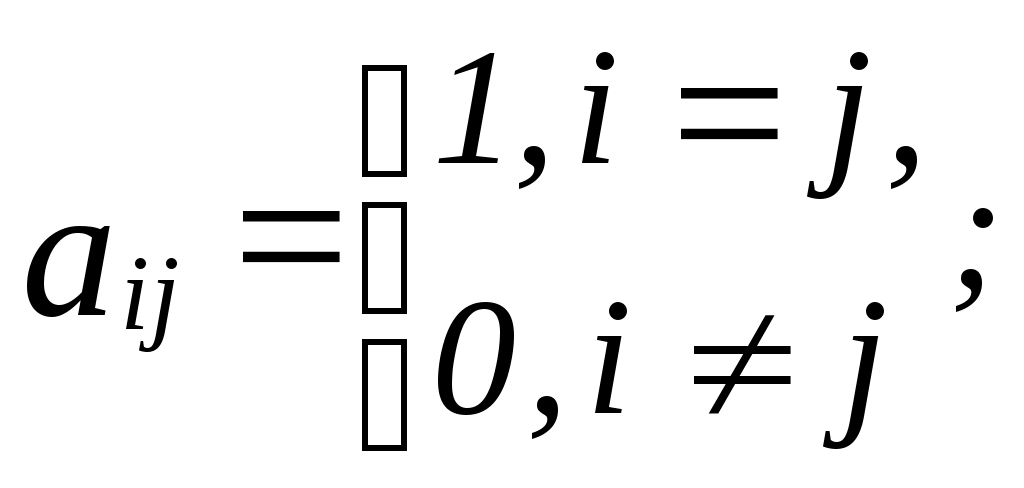 2) в графе G(E) присутствуют только петли при вершинах, других дуг нет; 3) 2) в графе G(E) присутствуют только петли при вершинах, других дуг нет; 3)Отношение R называется антидиагональным ( Примеры 3. 2.2. Операции над отношениями Вложение (включение). Отношение Дополнение. Отношение 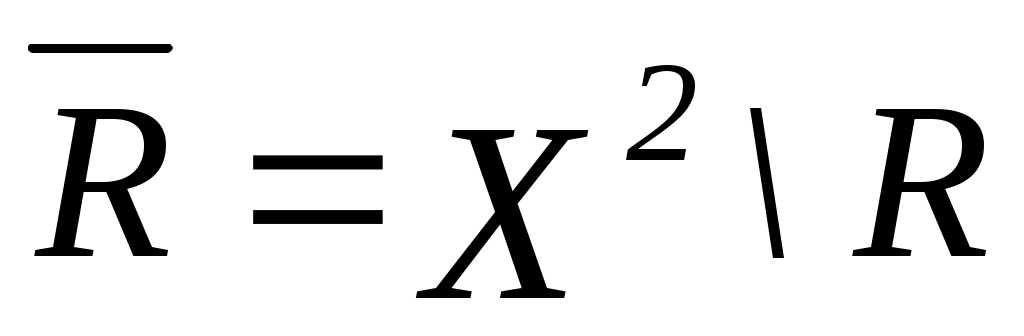 . .Справедливо: Пересечение. Пересечением отношений Объединение. Объединением отношений Обращение. Обратным к отношению R называется отношение Справедливо: Переход к двойственному отношению. Отношение Произведение. Произведением Сужение. Отношение Изоморфизм. Отношения Примеры Для отношений 1) Если 2) Если 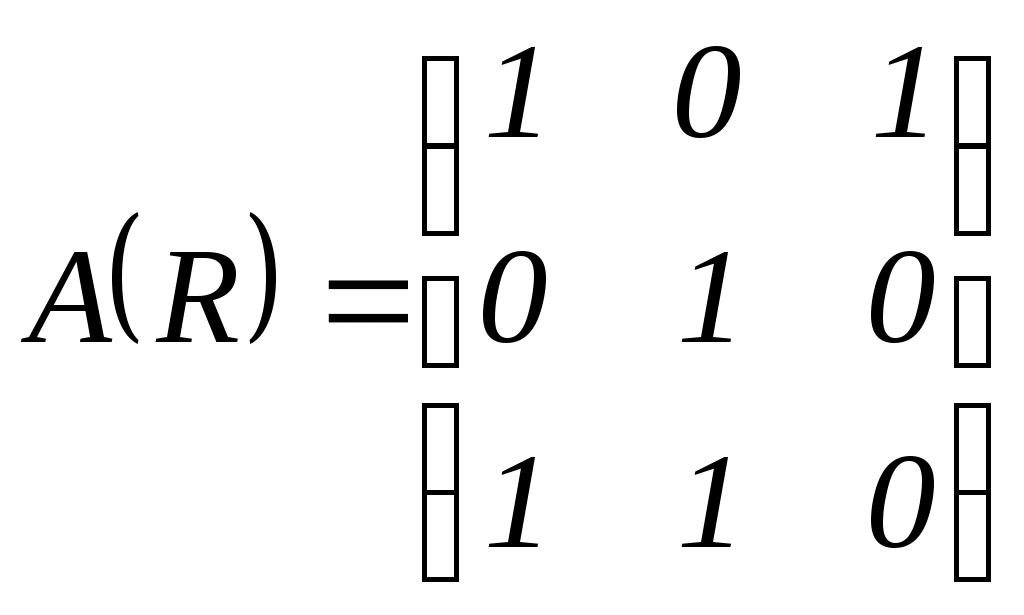 , то , то 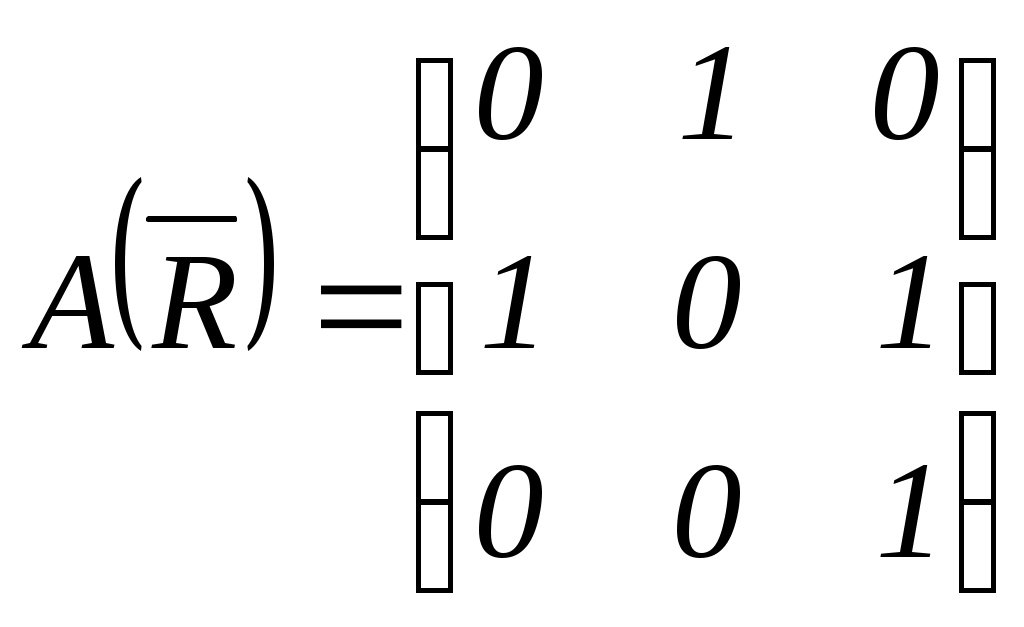 . . |
