численные методы. Задача принятия решений общая постановка, примеры
 Скачать 1.64 Mb. Скачать 1.64 Mb.
|
|
 Свойства СвойстваОтношения | Реф-лексив-ность | Анти-рефлек-сивность | Симмет-ричность | Асим-метрич-ность | Антисим-метрич-ность | Тран-зитив-ность | Связность |
| Толерантность | + | | + | | | | |
| Эквивалентность () | + | | + | | | + | |
| Доминирование (<<) | | + | | + | | | |
| Строгий порядок (<) | | + | | + | | + | |
| Нестрогий порядок ( | + | | | | + | + | |
| Линейный порядок | + | | | | + | + | + |
| Квазипорядок | + | | | | | + | |
Примеры
1. Отношение «быть похожим» является отношением толерантности.
2. Отношения «учиться на одном курсе», «иметь одинаковый остаток при делении на 3», отношение подобия являются отношениями эквивалентности.
3.Отношения «быть не ниже ростом»,
4.Отношения «быть старше»,
5. Отношение «выиграть матч» является отношением доминирования.
6. Отношение «быть не хуже» и отношение предпочтения являются отношениями квазипорядка.
2.5. Понятие R-оптимальности
Важное место в теории выбора и принятия решений занимает понятие «лучшего элемента». Для формализации этого понятия введем в рассмотрение следующие определения.
Элемент x
Элемент x
Элемент
Множество мажорант обозначается
Примеры
1. Отношение
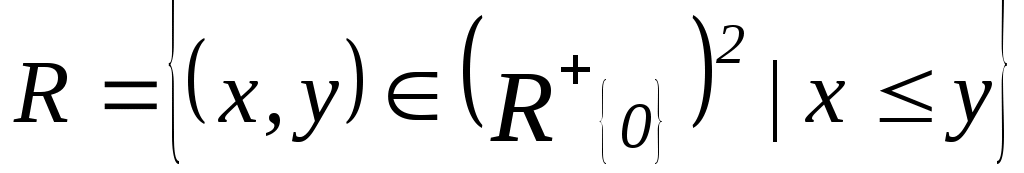 имеет минимум x=0 (так как
имеет минимум x=0 (так как 2.6. Метризованные бинарные отношения
При анализе экспертной информации традиционных типов бинарных отношений, описываемых в п.2.3, может оказаться недостаточным. Суждения эксперта часто содержат не только качественные оценки предпочтительности альтернатив или их эквивалентности, но и количественные оценки степени предпочтительности одной альтернативы над другой или степени эквивалентности пары альтернатив.
Метризованным отношением
Граф метризованного бинарного отношения отличается от графа бинарного отношения R наличием числа
Матрицей смежности бинарного отношения является квадратная матрица
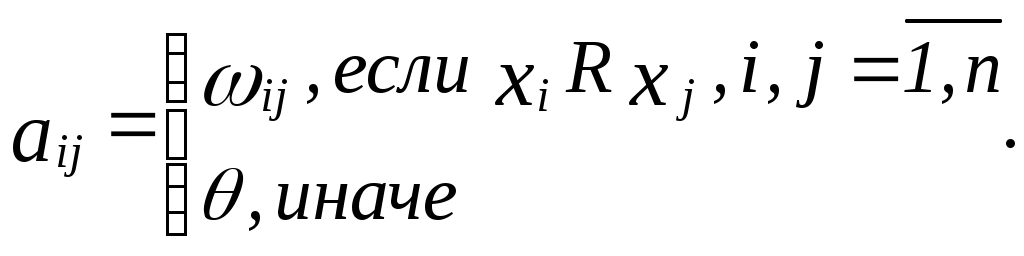
Метризованное отношение
Метризованное отношение
Метризованное отношение
Для метризованного аддитивного бинарного отношения числа
Матрицу аддитивного метризованного отношения квазипорядка
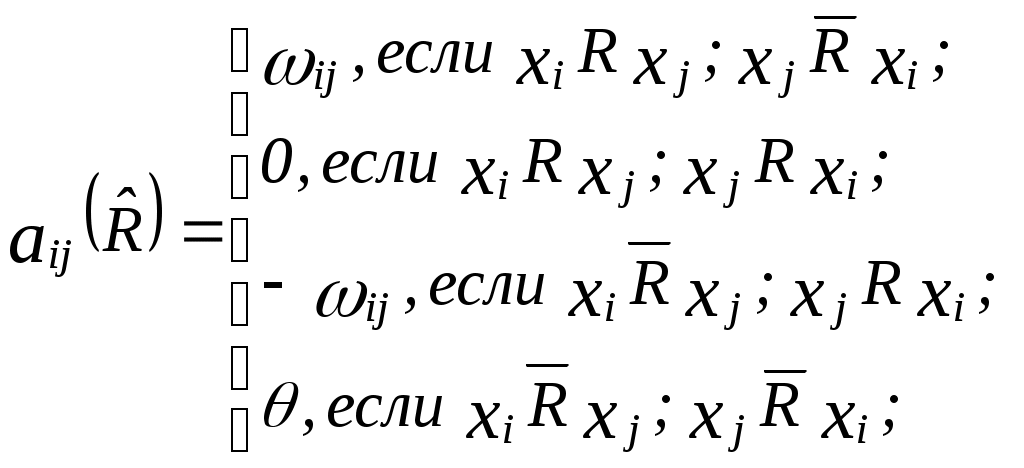
а матрицу мультипликативного отношения квазипорядка
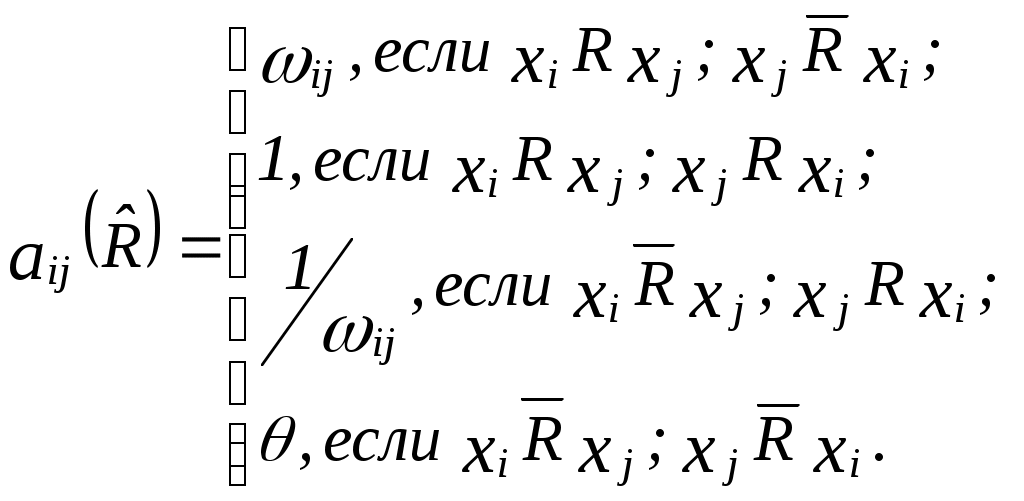
Примеры
Аддитивным метризованным отношением квазипорядка является отношение, заданное следующим графом:
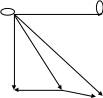 3
3 
0
5 2 4
 3 2
3 20 0 0
Матрица данного отношения имеет вид:
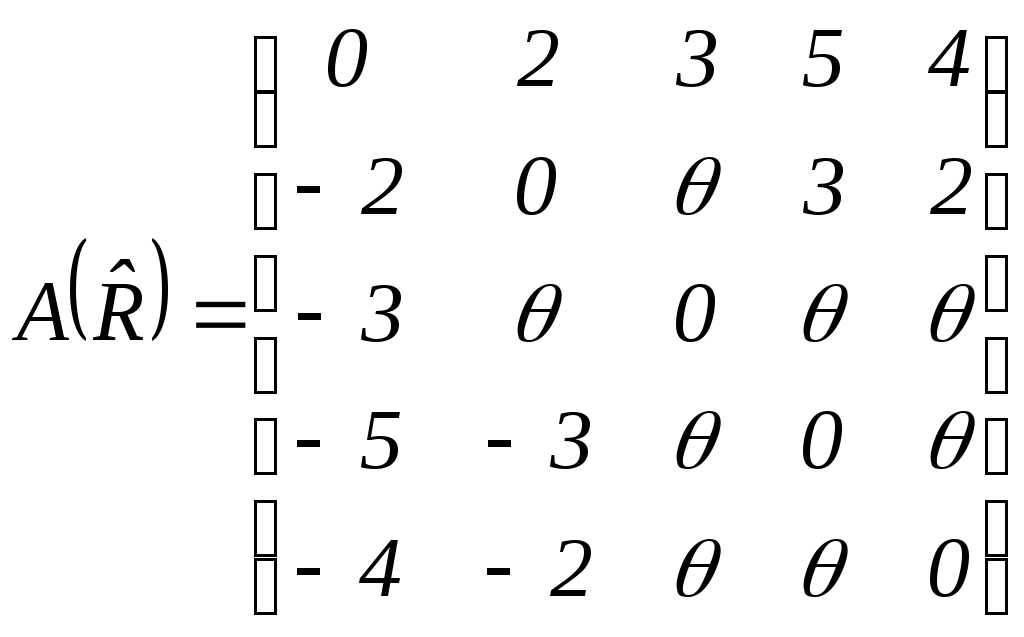 .
.2. Мультипликативным метризованным отношением квазипорядка является отношение, заданное следующим графом:


 1
16 4
 1 1
1 1

2 3
1

Матрица данного отношения имеет вид:
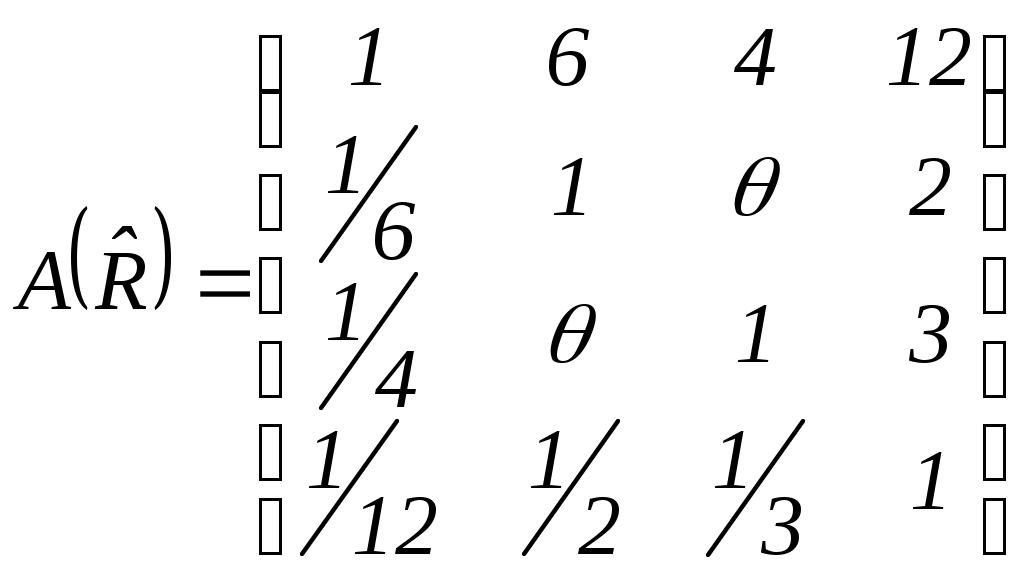 .
.Упражнения к § 2
Основные упражнения
1. Пусть
1) матрицей; 2) сечениями.
2. Пусть
2)
3. Доказать, что
4. Доказать, что
5. Доказать, что для любых отношений
6. Доказать, что
7. Доказать, что
8. Рассмотрим матрицу
9. Бинарные отношения
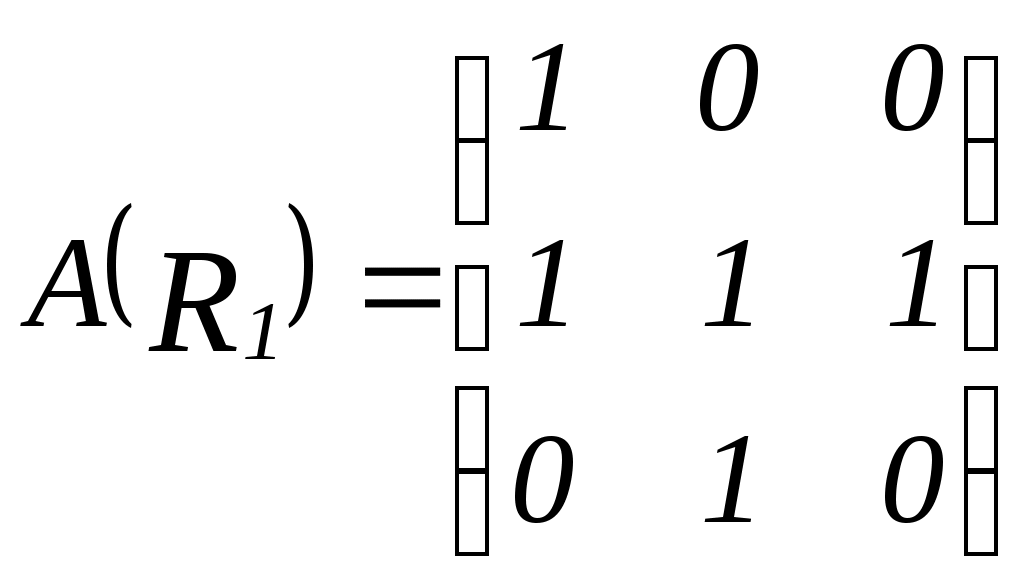 ,
, 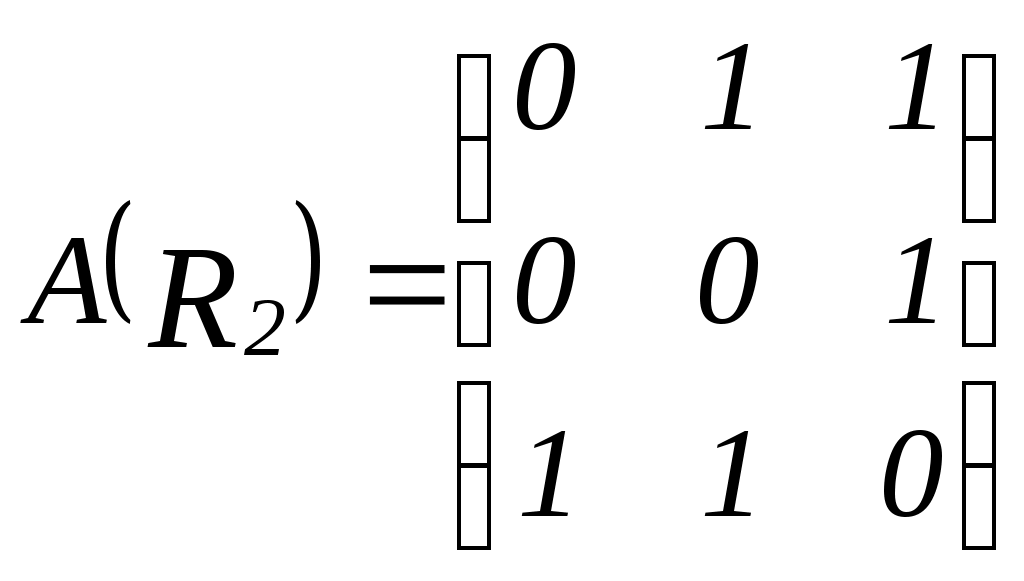 .
. Построить матрицу отношения
Доказать, что отношение R симметрично тогда и только тогда, когда
11. Доказать, что если отношение R асимметрично, то оно антирефлексивно.
12. Найти максимум, минимум, миноранты, мажоранты бинарных отношений, заданных графами:
1)

;
b c
2
 )
) ;
b c
 :
: 
 a
ab c .
13. Доказать, что максимум по частичному порядку единственен. Верно ли это утверждение для произвольного R?
14. Могут ли одновременно существовать : 1) максимумы и мажоранты; 2) минимумы и миноранты.
15. Доказать, что: 1)
16. Бинарные отношения, заданными графами, дополнить до аддитивных и мультипликативных метризованных отношений квазипорядка:
1)

 2
22 3
2)


5
2 4 4
II. Дополнительные упражнения
Пусть
а) матрицей смежности; b) графом; c) сечениями.
Изобразить на плоскости следующие бинарные отношения:
10)
11)
12)
Выписать верхние и нижние сечения бинарных отношений из пп. 1), 2), 4), 6), 7), 11).
Вывести формулу, выражающую нижнее сечение
Какими особенностями обладают матрица, граф, сечения антидиагонального отношения?
Сколько можно выписать матриц смежности для бинарного отношения, заданного на множестве n элементов? Показать, что отношение R, для которого матрица A(R) не зависит от нумерации элементов множества , либо пустое, либо полное, либо диагональное, либо антидиагональное.
Для отношений из №2 указать полные, пустые, диагональные, антидиагональные отношения.
Для бинарных отношений из № 2 выписать все пары вложенных отношений. Указать все пары взаимодополнительных отношений. Для пп. 1) – 5) выписать дополнительные, обратные и двойственные отношения.
Для бинарных отношений из №1 найти: дополнение, пересечение, объединение, обратные, двойственные отношения, произведение отношений. Для каждого бинарного отношения найти матрицу смежности, граф, сечения.
Доказать, что для любых
Доказать, что
Отношения R и
1)
Какой вид имеет отношение
Для отношений
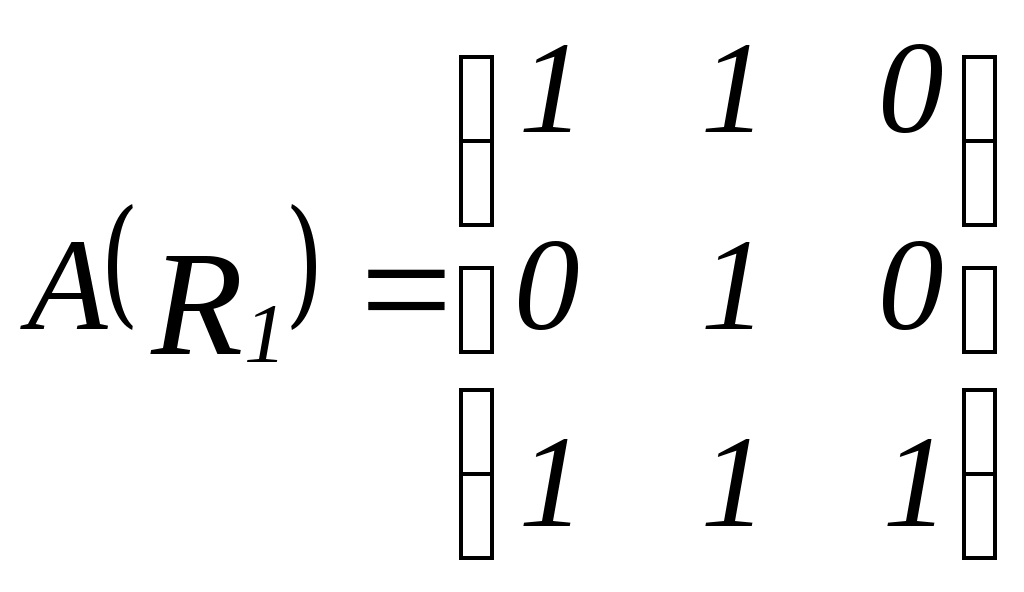 ;
; 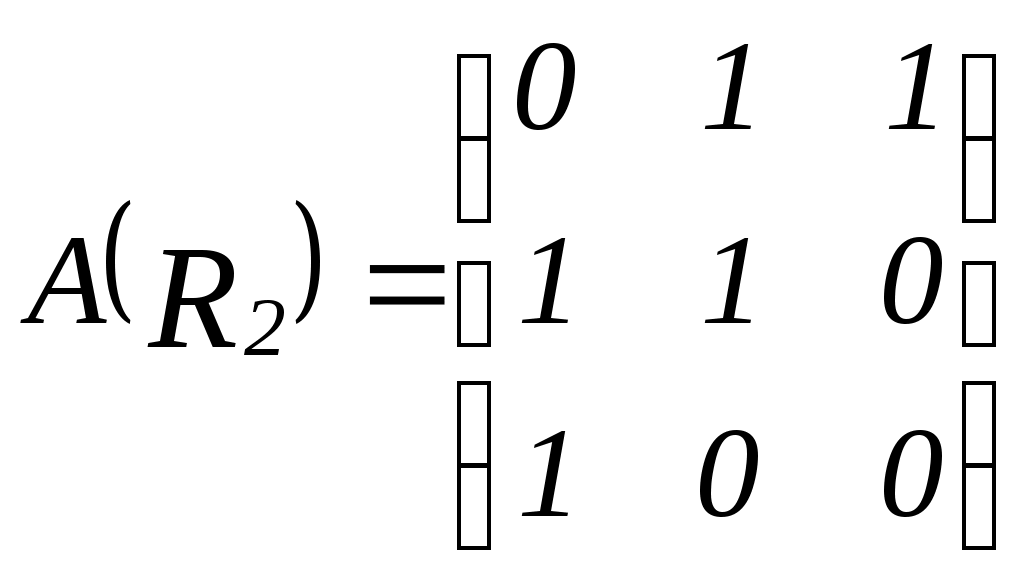 , найти
, найти Доказать, что если R рефлексивно, то
Доказать, что для рефлексивного отношения R транзитивность эквивалентна равенству
Какие из отношений №2 являются транзитивными?
Привести пример антисимметричного отношения, которое при этом не симметрично и не асимметрично.
Описать отношение, являющееся одновременно симметричным и антисимметричным.
Привести пример отношений, обладающих в точности одним, двумя, тремя и четырьмя свойствами из числа следующих: рефлексивность, симметричность, транзитивность, антисимметричность.
Показать, что всякое ацикличное отношение асимметрично.
Сформулировать условия на матрицу, граф и сечения отрицательно транзитивного отношения.
Пусть R – отношение эквивалентности на множестве
23.Для бинарных отношений, заданных на множестве
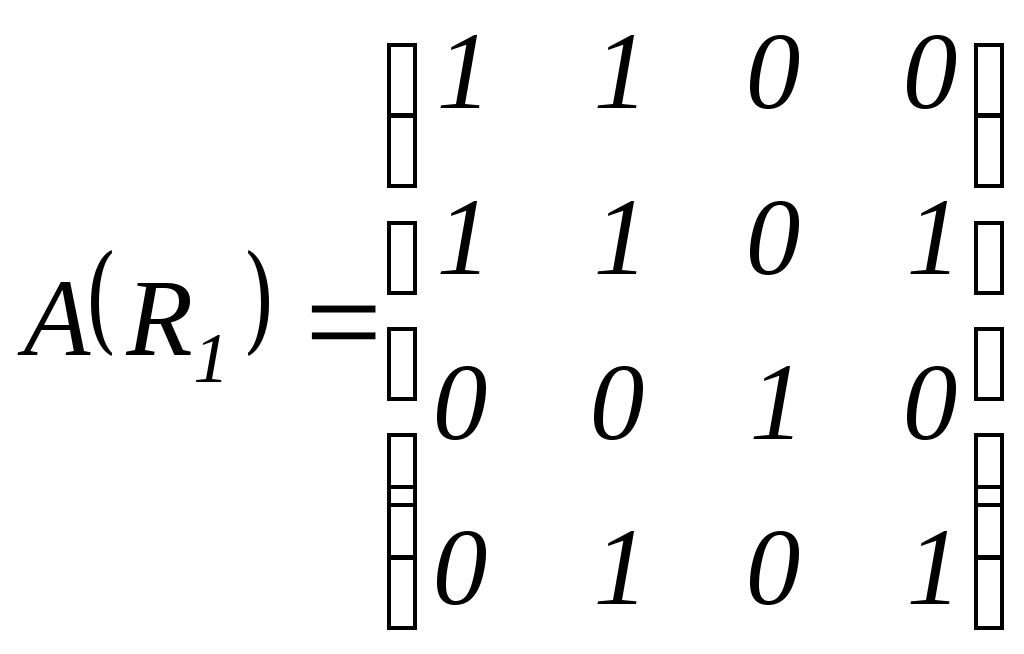 ; 2)
; 2) 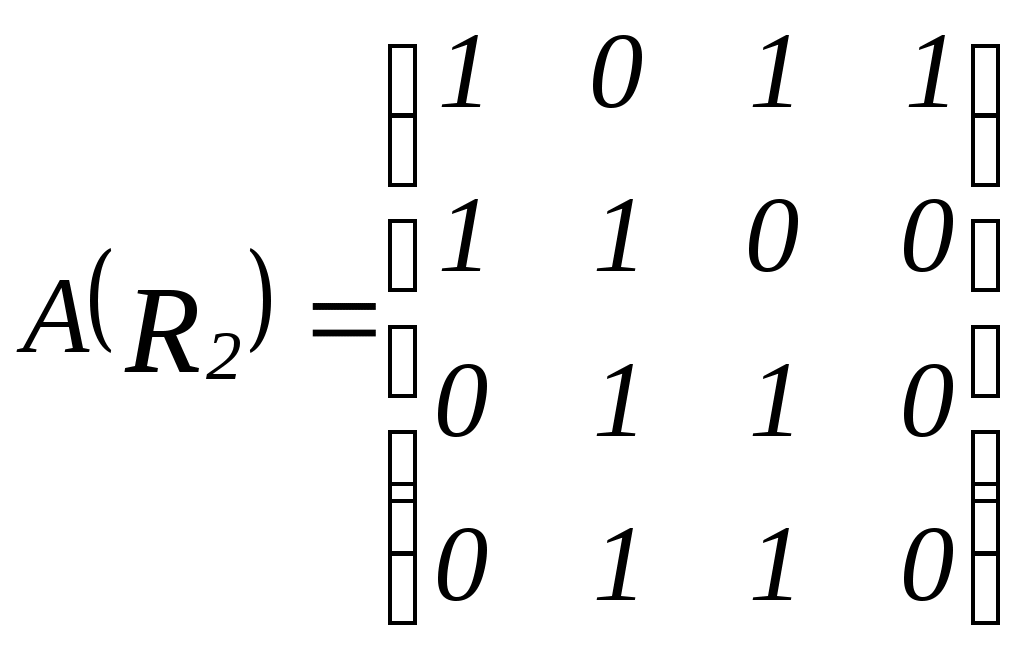 ; 3)
; 3)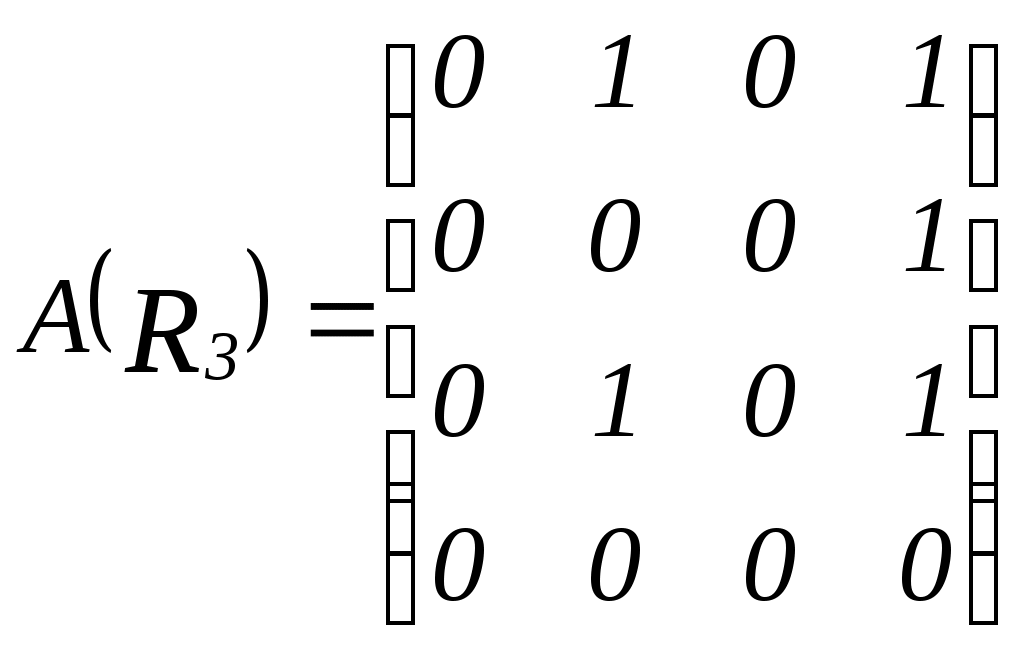 ; 4)
; 4) 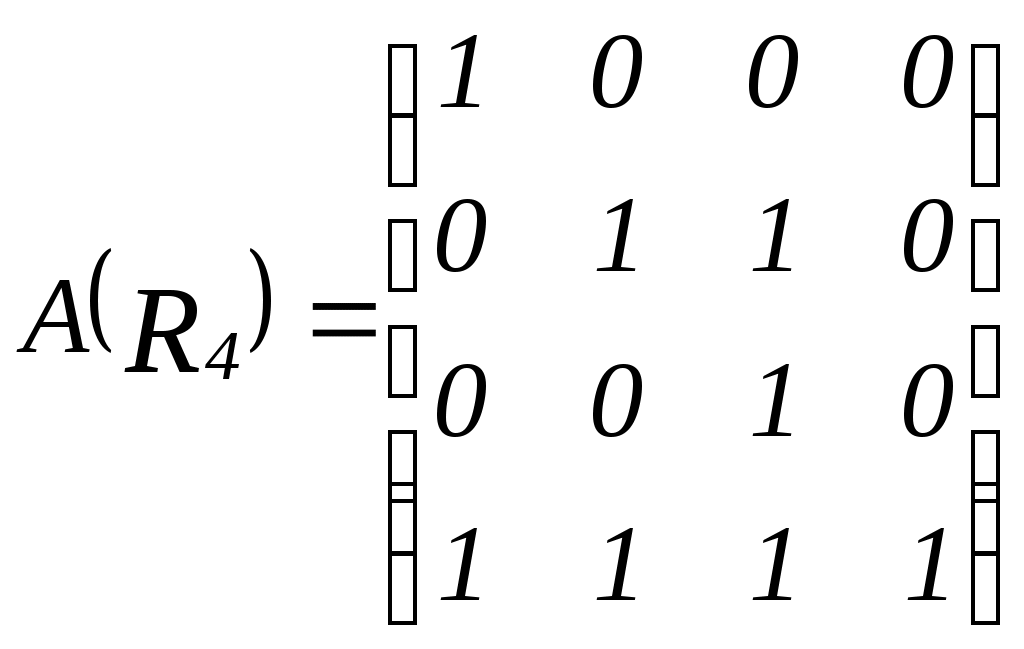 ;
; 5)

6)
1
 3
34 .
Являются ли перечисленные отношения отношениями эквивалентности, строгим порядком, нестрогим порядком, квазипорядком, доминированием?
24.Пусть R – произвольное отношение на множестве . Доказать:
25. Найти максимумы, минимумы, мажоранты, миноранты для следующих бинарных отношений:
1) a d

;
 f
fc
b g
 b
b2) c
;
a d
3)
a b .

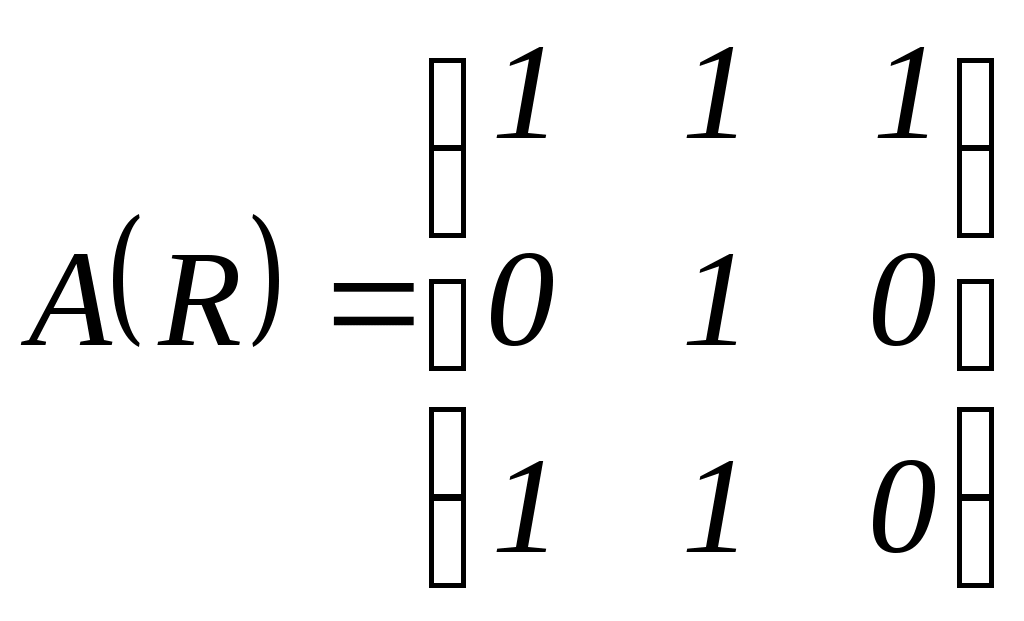 , то
, то 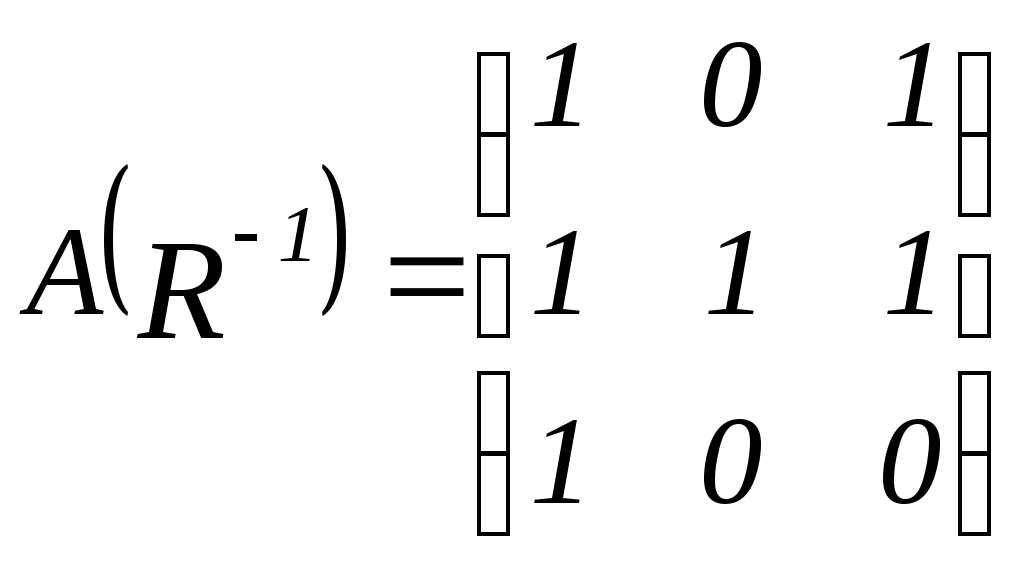 .
.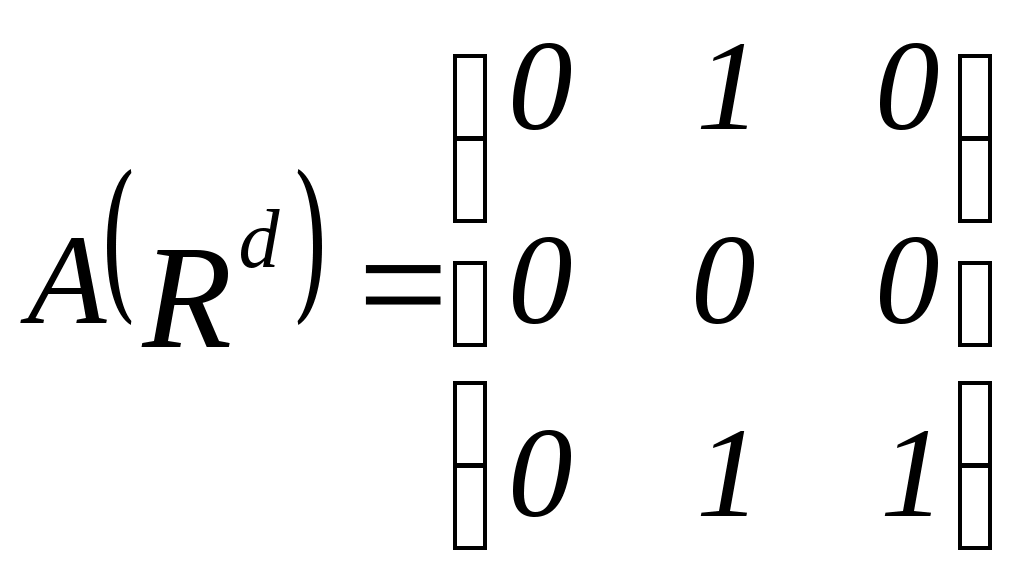 .
. 1 2
1 2