численные методы. Задача принятия решений общая постановка, примеры
 Скачать 1.64 Mb. Скачать 1.64 Mb.
|
Классификация задач принятия решенийЗадачи принятия решений классифицируют в зависимости от имеющейся информации о множестве Задача с известными В практических задачах выбор лучших альтернатив осуществляется на основе их свойств. Предположим, что для альтернатив известны их свойства (характеристики) Если 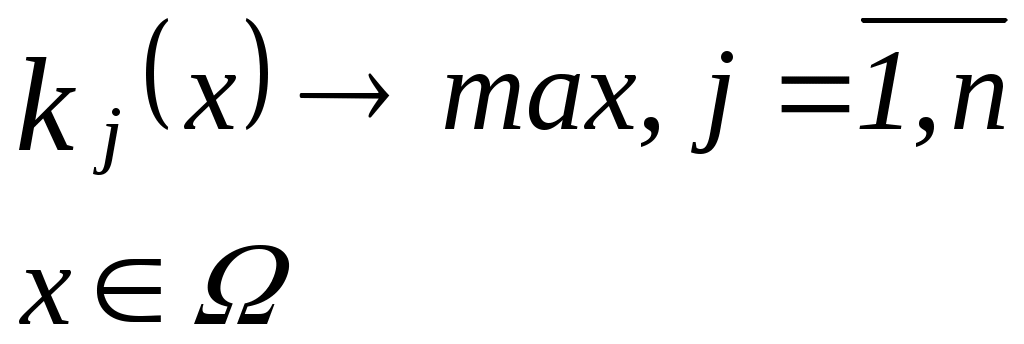 . .Особый класс задач принятия решений составляют игровые задачи – задачи разрешения конфликтных ситуаций. Данный класс задач изучается в рамках математической теории игр. Игровые модели – это модели принятия решений в условиях неопределенности, когда принимающий решение субъект ("игрок") располагает информацией лишь о множестве возможных ситуаций, в одной из которых он действительно находится, о множестве решений ("стратегий"), которые он может принять, и о количественной мере того "выигрыша", который он мог бы получить, выбрав в сложившейся ситуации определенную стратегию. Неопределенность, как правило, является сознательной деятельностью другого лица (лиц), отстаивающего свои интересы. Классификацию задач принятия решений можно представить в виде следующей схемы: 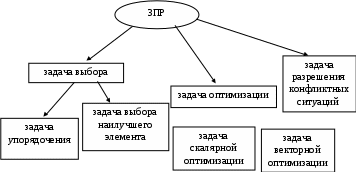   ПримерыУпорядочение альтернатив. Для ряда задач представляется вполне обоснованным требование определить порядок на множестве альтернатив. Например, упорядочение научных работ сотрудников исследовательского центра по значимости, упорядочение абитуриентом вузов по приоритетности. Задача выбора наилучшего элемента. К данному типу относятся, например, следующие задачи: Выбор дачи для летнего отдыха. Множеством альтернатив является множество дач, сдаваемых внаем по приемлемой для снимающих цене. В качестве критериев могут выступать качество дачи, наличие магазина недалеко от дачи, расстояние до города. В данной задаче возможно появление новых альтернатив в процессе поиска дач и новых критериев сравнения вариантов по мере осмотра имеющихся альтернатив. Принципом оптимальности может служить, например, один из следующих принципов: расстояние до города должно быть минимально, число магазинов – максимально, дача должна обладать максимальным уровнем качества; наличие магазина в радиусе 1 километра от дачи, расстояние до города менее 30 километров, качество дачи – максимальное; качество дачи – не ниже определенного уровня, расстояние до города – минимально возможное. Выбор из группы студентов 4 курса факультета ПММ одного студента для поездки на обучение за границу. 3. Задача скалярной оптимизации Рассмотрим задачу формирования ассортиментного плана предприятия. Предположим, что предприятие выпускает n видов продукции ( Обозначим через 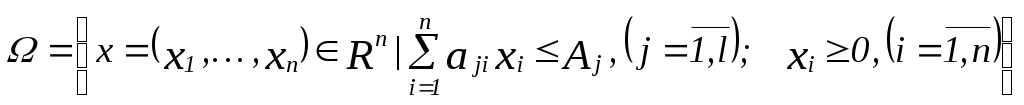 . В качестве принципа оптимальности можно выбрать максимизацию суммарной прибыли от произведенной продукции: . В качестве принципа оптимальности можно выбрать максимизацию суммарной прибыли от произведенной продукции: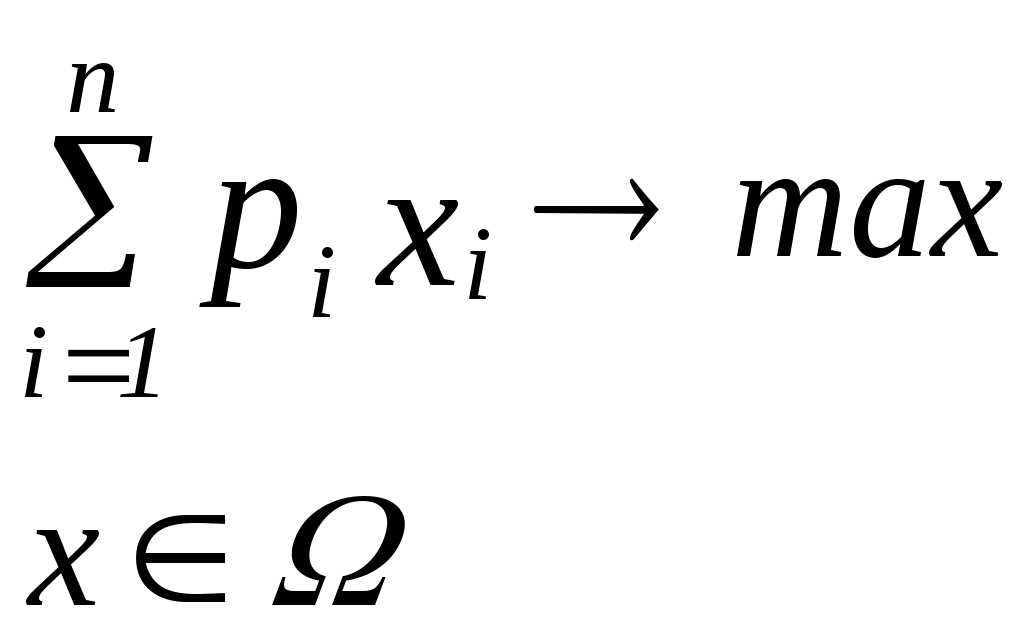 . .3. Задача векторной оптимизации. Рассмотрим задачу потребления. Имеется некоторый потребитель, располагающий доходом I. Для потребления он может приобрести n продуктов ( Множество альтернатив в задаче имеет вид: 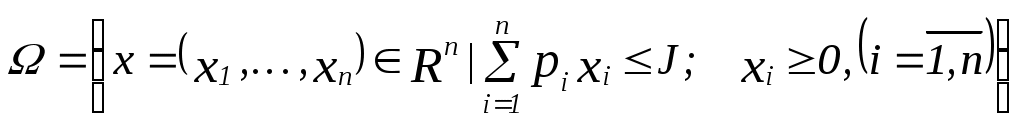 . В качестве критериев можно выбрать: максимизация полезности от потребления набора продуктов; . В качестве критериев можно выбрать: максимизация полезности от потребления набора продуктов; минимизация денежных затрат на приобретение продуктов: 4. Задача разрешения конфликтных ситуаций. Рассмотрим простейший класс игровых моделей – матричные игры. Пусть имеется два игрока P1 и P2 . P1 может выбрать один из двух вариантов действий, P2 – один из трех вариантов. Известен выигрыш Требуется определить оптимальные стратегии обеих игроков. P1 уверен, по крайней мере, в получении выигрыша |
