численные методы. Задача принятия решений общая постановка, примеры
 Скачать 1.64 Mb.
|
|
§3. Функции выбора 3.1. Понятие функции выбора. Функции выбора, порожденные бинарными отношениями Пусть задано множество  , X – произвольное подмножество данного множества  . Рассмотрим множество всех подмножеств :  .Функцией выбора называется отображение  , ставящее в соответствие каждому  его подмножество  .C()=, ситуация C(X)= означает «отказ от выбора». Предположим, что на множестве задано бинарное отношение  . Бинарное отношение порождает две наиболее важные в теории выбора функции: блокировку и предпочтение.Функция выбора, определяемая на каждом подмножестве X множества следующим образом:  , (1)называется блокировкой. Функция выбора:  (2)называется предпочтением. Пусть R – бинарное отношение на ;  - его сужение на . Тогда  состоит из всех мажорант  , а  - из всех максимумов, т.е.  ,  .В силу задачи №2 (см. упражнения к § 3) из двух функций выбора, порожденных бинарным отношением R, достаточно рассматривать только одну, так как блокировка по отношению R совпадает с предпочтением по отношению  и наоборот.Функция выбора C называется нормальной, если существует бинарное отношение  такое, что  или  .Отметим, что если существует R: , то в силу задачи №2 существует  такое, что  и наоборот.Функция выбора  вложена в функцию выбора  ( ), если  ,  .Если  и неверно, что  , то строго вложена в ( ).Пусть  - цепочка строго вложенных функций выбора.Цепочка называется максимальной, если не существует другой цепочки, в которую она входит как часть. Ближайшей к С сверху (снизу) называется функция выбора  ( ) такая, что  ( ) и не существует  ( ) такой, что  ( ).Примеры1. В задаче №5 (см. упражнения):  .2. В задаче № 5: - ближайшая сверху для ; - ближайшая снизу для ; не является ближайшей сверху для , так как .Логические формы функций выбора Рассмотрим конечное множество :  ; – про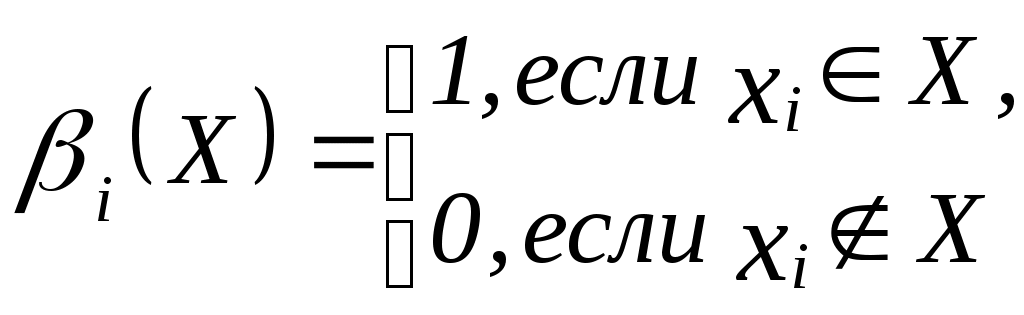извольное подмножество. Каждому подмножеству ( ) поставим в соотвестствие n-мерный вектор с компонентами 0 и 1 по формулам:  , (3)где  .Отметим, что  ()= (0,…,0);   =(1,…,1).Логической формой функции выбора (ЛФВ (С)) называется упорядоченный набор булевых функций  от n-1 переменных :  ,  , построенных по следующему правилу:   , (4)где  ,   ;  .Задание ЛФВ (С) эквивалентно заданию функции выбора С. Замечание 1. Формула (4) означает, что 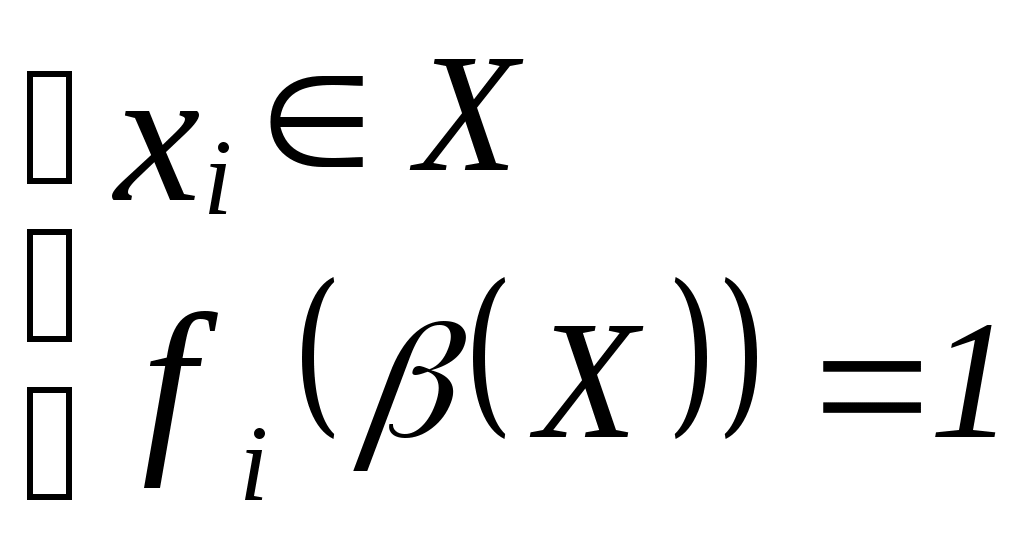  .То есть: если  , что эквивалентно тому, что  , то  ;если  , что эквивалентно тому, что  и, следовательно,  , то (4) верна для любого значения  .Алгоритм 1 (формирование ЛФВ (С)). Задано множество ;  - множество всех подмножеств , С- функция выбора, заданная на  .Для каждого подмножества 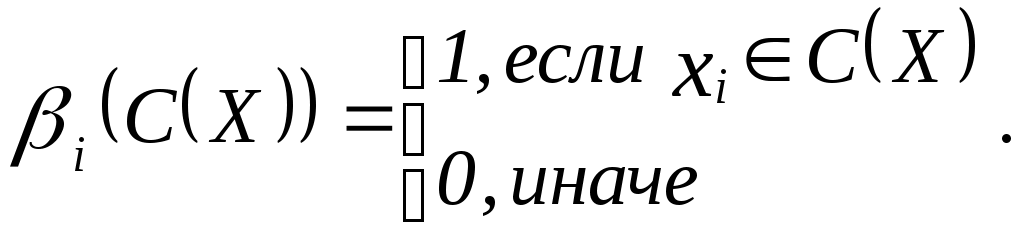формируется n-мерный вектор по формулам (3).Для каждого подмножества формируется n-мерный вектор  , где  Формирование таблиц значений булевых функций  ,  для всевозможных значений булевых переменных  :
 по формуле (4) в силу замечания 1 рассматриваем набор  . Тогда =1   . Формирование совершенных дизъюнктивных нормальных форм функций  , :  .ЛФВ (С), представляющая семейство функций  , построена.3.3. Операции над функциями выбора Над функциями выбора определены следующие операции. Объединением функций выбора  и  называется функция  , определяемая формулой:  , .Пересечением функций выбора и называется функция  , определяемая формулой:  ,  .Дополнением функции выбора С называется функция 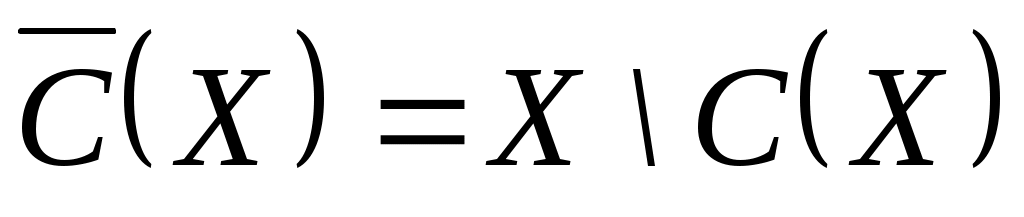, определяемая формулой:  , .Произведением функций выбора и называется функция  , определяемая формулой:  , .Теорема 1. Пусть 1) ; 2)  ; 3)  . Тогда для любого  справедливо: ; 2)  ; 3)  .Теорема 2. Пусть  . Тогда    .3.4. Классы функций выбора В основу классификации функции выбора положены следующие условия. Условие наследования (Н). Функция выбора С удовлетворяет условию наследования, если из того, что  , следует:  .Условие независимости от отвергнутых альтернатив (О). Функция выбора С удовлетворяет условию независимости от отвергнутых альтернатив, если из того, что  , следует:  .Условие согласия (С). Функция выбора С удовлетворяет условию согласия, если  .Условие Плотта (квазисумматорность) (КС). Функция выбора С удовлетворяет условию квазисумматорности, если  ,  .Условие сумматорности (СМ). Функция выбора С удовлетворяет условию сумматорности, если  , .Условие мультипликаторности (МП). Функция выбора С удовлетворяет условию мультипликаторности, если  , .Условие монотонности (М). Функция выбора С удовлетворяет условию монотонности, если   .Функция выбора называется: Рефлексивной, если  =,  .Антирефлексивной, если = , .Полной, если  для всех ,  .Транзитивной, если из того, что 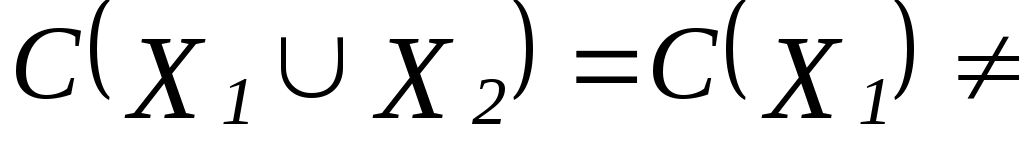 ,  следует, что  .Легко проверить, что функция выбора из задачи №10 (см. упражнения к § 3) является антирефлексивной, полной, транзитивной. 3.5. Динамические функции выбора В предыдущих пунктах рассматривались функции выбора, в которых выбор на предъявляемых подмножествах определялся ими самими и свойствами функции выбора. Однако возможны ситуации, когда на выбор оказывает влияние уже ранее сделанный выбор. Будем считать, что подмножества X множества предъявляются для выбора последовательно:  . Упорядоченность подмножеств связана с моментом предъявления данного множества. Пусть  - результаты выборов,  .Динамической функцией выбора называется функция  ,  , зависящая от предъявляемого множества  и предшествующего выбора  :  , ;  - заданное начальное состояние.Динамическая функция выбора представляет собой конечный автомат, задаваемый множеством S состояний, множеством O входов и функцией переходов  :  , ;  - начальное состояние.Конечным автоматом, порожденным выбором, называется автомат, у которого множество состояний S есть множество всех возможных выборов из всех подмножеств , а множество входов – множество всех подмножеств (т.е. ). Функция переходов F определяется выбором из X при условии, что предыдущим выбором было некоторое Y. |
