численные методы. Задача принятия решений общая постановка, примеры

• Название: Задача принятия решений общая постановка, примеры
• Анкор: численные методы
• Дата: 17.11.2021
• Размер: 1.64 Mb.
• Имя файла: Chast_1 (1).doc
• Тип: Задача; #274613
• страница: 6 из 7

Способы задания динамической функции выбора

1. 
   Таблица переходов.
   

o s		…
…

Строки таблицы соответствуют состояниям, столбцы – входам; на пересечении строки и столбца находится состояние, в которое состояние, соответствующее строке, перешло под воздействием входа, соответствующего столбцу.

2. 
   Диаграмма переходов.
   

Диаграмма переходов представляет собой граф, вершинами которого являются состояния. Вершины i, j связаны дугой, если возможен переход из состояния i в состояние j. Над дугой помечается, под действием каких входов данный переход возможен.

Упражнения к § 3

1. 
   Основные упражнения
   

1. Пусть - сужение отношения R, заданного на , на множество ; - отношение двойственное к ; - отношение двойственное к ; - отношение двойственное к R; - сужение на X. Доказать, что .

2. Доказать, что функции выбора и связаны соотношениями: 1) ; 2) .

3. Верно ли, что из того, что , следует, что ?

4. Доказать, что произвольная функция выбора не обязательно является нормальной.

5. Рассмотрим . Для перечисленных ниже функций выбора C, заданных на , построить отношения , такие, что или доказать, что таких , не существует:

1. 
   , , ;
   
2. 
   , =, ;
   
3. 
   , =, .
   

6. Пусть и задана функция выбора: , , , , , , . Построить ЛФВ (С).

7. Пусть и задано семейство булевых функций: = ; , . Найти функцию выбора С.

8. Для функции выбора из задачи 6 и функции из задачи 7 построить функции выбора:

1) ; 2) ; 3) ; 4) . Найти ЛФВ построенных функций.

9.Пусть , - нормальные функции выбора. Доказать, что - нормальная функция выбора.

10. Пусть . Для функции выбора С: , , проверить выполнение условий Н, О, С, КС, СМ, МП, М.

11. Пусть . Функция выбора описывается следующим образом:

если предъявляется x и предыдущий выбор не содержал x, то выбирается x, в противном случае выбор пуст; если предъявляется y и предыдущий выбор содержал y, то выбирается y, в противном случае выбор пуст; если предъявляется и предыдущий выбор не был пуст, то выбирается y, в противном случае выбирается x. Задать функцию выбора: 1) таблицей; 2) диаграммой перехода.
II. Дополнительные упражнения

1. 
   Пусть . Для всевозможных функции выбора, заданных на и перечисленных в таблице, построить отношения и такие, что , или доказать, что таких бинарных отношений не существует.
   

№

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

x

x

x

x

x



x

x





x











y

y

y

y



y





y

y



y









x,y

x

y



x,y

x,y

x

y

y

x





x,y

x

y



Для найденных бинарных отношений указать все пары двойственных.

2. Для функций выбора 1-16 из № 1 указать ближайшие сверху и ближайшие снизу функции выбора. Найти длину максимальной цепочки вложенных функций выбора.

3. Доказать, что  для любого тогда и только тогда, когда отношение R – ациклично.

4. 
   Пусть и – бинарные отношения, заданные на , такие, что . Доказать, что . Верно ли утверждение: ?
   
5. 
   На множестве функций выбора, заданных на , рассмотрим бинарное отношение R: . Доказать, что R – отношение частичного порядка.
   
6. 
   Найти длину максимальной цепочки вложенных функций выбора для множества 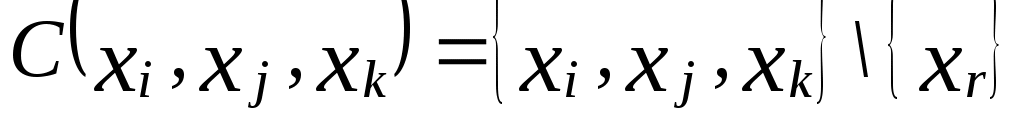, состоящего из n элементов.
   
7. 
   Пусть и задана функция выбора: ; , где ; , где ; . Построить ЛФВ (С).
   
8. 
   Найти ЛФВ для функций выбора из № 1.
   
9. 
   Пусть . Доказать, что число различных функций выбора на равно .
   
10. 
    Пусть и задано семейство булевых функций : ; ; ; . Построить функцию выбора С по ее ЛФВ (С)= .
    
11. 
    Пусть и задано семейство булевых функций : ; ; ; . Построить функцию выбора С по ее ЛФВ (С)= .
    
12. 
    На множестве заданы функции выбора и :
    

X	x	y	z	x,y	x,z	y,z	x,y,z
	x		z	x	x	y	z
		y	z	x	x,z	z	x,y

Построить : 1) ; 2) ; 3) ; 4) . Найти ЛФВ построенных функций.

4. 
   Для функции из № 7 и из № 10 построить : 1) ; 2) ; 3) ; 4) . Найти ЛФВ построенных функций.
   
5. 
   Какими из условий : Н, О, С, КС, СМ, МП обладают функции выбора 1) из № 1; 2) из № 12. Являются ли данные функции рефлексивными, антирефлексивными, полными, транзитивными?
   
6. 
   Доказать, что классы Н О С, О С не являются пустыми.
   
7. 
   Доказать строгое включение: СМ Н О С.
   
8. 
   Рассмотрим турнирное правило. Проводится круговой турнир. Пусть каждая команда один раз встречается с каждой и в каждой игре возможно 3 исхода: выигрыш, поражение или ничья. Для каждой команды число очков определяется как число выигрышей минус число проигрышей, и победителем объявляется тот, у которого эта величина максимальна. К каким классам относится функция выбора, задаваемая следующей турнирной таблицей:
   

   №	команды	1	2	3	4	5	6	7	8	9	10
   1	Торпедо	-	2:3	1:0	2:0	1:1	2:0	1:0	0:1	2:2	1:0
   2	Динамо (К)		-	0:0	1:1	0:1	1:1	1:2	3:2	3:1	3:0
   3	Динамо (Тб)			-	1:0	3:1	0:0	0:0	1:1	0:0	2:0
   4	Зенит				-	1:2	3:3	1:0	5:3	2:1	0:0
   5	Динамо (М)					-	1:2	1:0	0:0	0:1	2:0
   6	ЦСКА						-	0:1	1:1	1:2	1:2
   7	Локомотив							-	3:0	1:3	1:0
   8	Арарат								-	2:3	2:1
   9	Спартак									-	1:1
   10	Динамо (Мн)										-

9. 
   Каким из классов может пинадлежать любая турнирная функция выбора?
   

19.В магазине могут продаваться 2 продукта: кефир и ряженка. Покупатель ходит ежедневно в один и тот же магазин и покупает не более одного из перечисленных продуктов. Покупатель также не желает покупать два дня подряд один и тот же продукт, для него лучше сделать в этом случае перерыв и не покупать ничего. Если же в предыдущий день он не покупал ничего и в магазине имеется и кефир, и ряженка, то он выберет кефир. Построить функцию выбора покупателя, задав ее таблицей и диаграммой переходов.