|
|
численные методы. Задача принятия решений общая постановка, примеры
§ 4. Задача выбора
Задача выбора, как показано в § 1, является частным случаем более общей задачи принятия решений 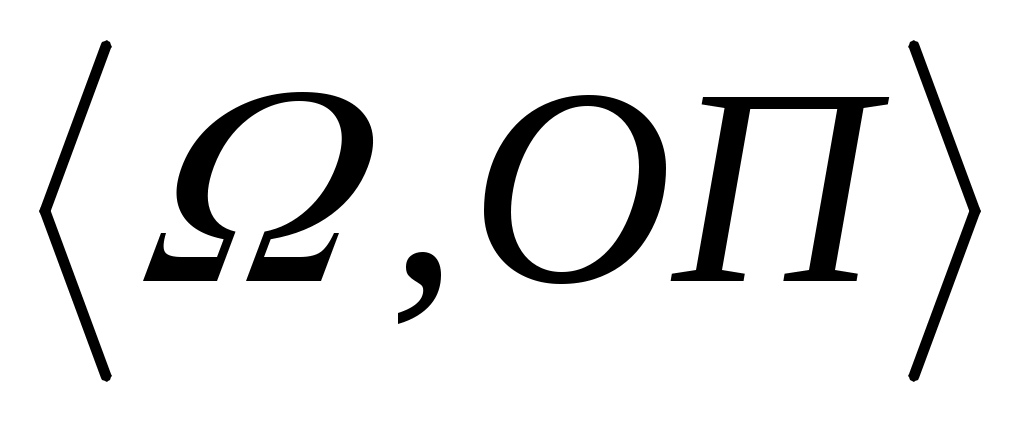 , когда исходное множество альтернатив , когда исходное множество альтернатив 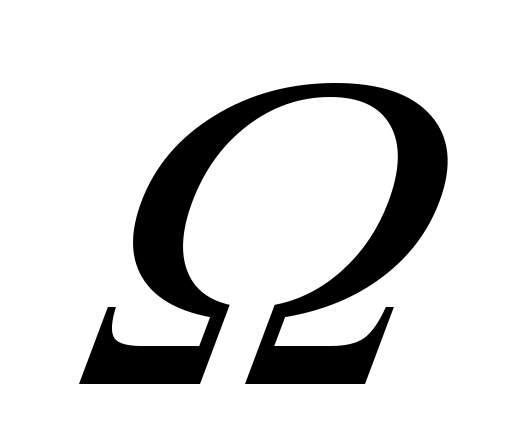 известно. известно.
Задача выбора называется простой, если ее решение 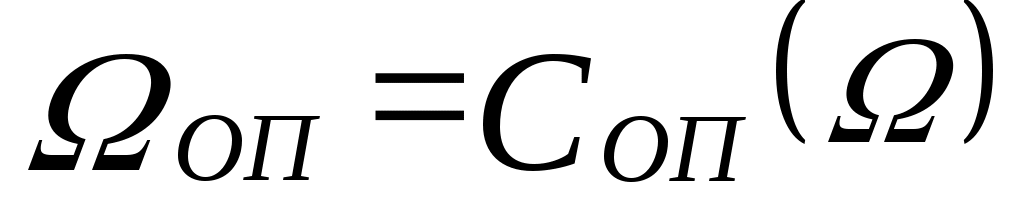 может быть найдено непосредственно (например, указано ЛПР). Для решения простых задач выбора не требуется использования специальных алгоритмов. В противном случае задачу выбора сводят к математической задаче выбора. может быть найдено непосредственно (например, указано ЛПР). Для решения простых задач выбора не требуется использования специальных алгоритмов. В противном случае задачу выбора сводят к математической задаче выбора.
Математическая задача выбора
Будем считать, что ЛПР известны: 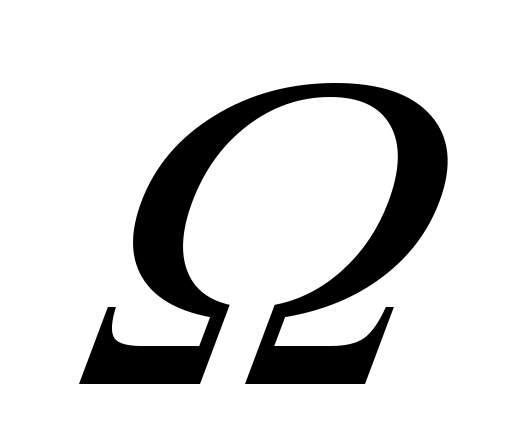 – множество альтернатив, – множество альтернатив, 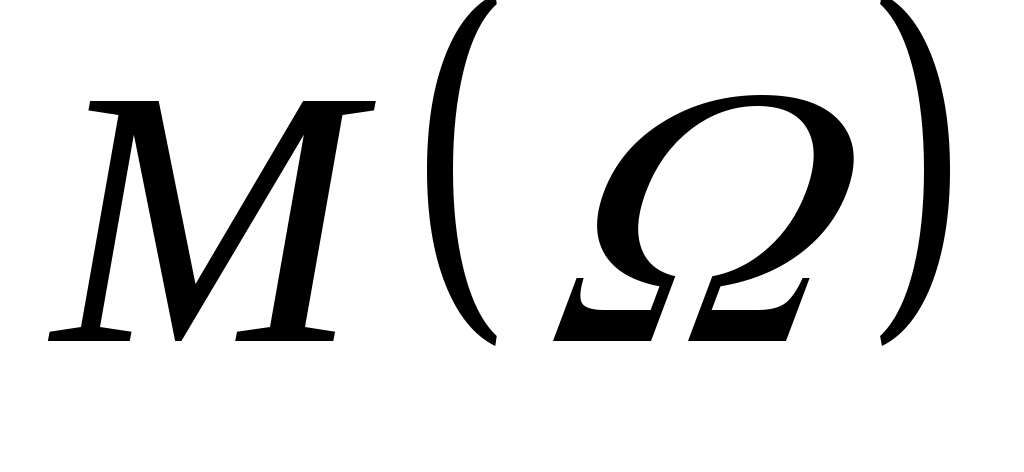 – множество функций выбора, которые могут быть построены на – множество функций выбора, которые могут быть построены на 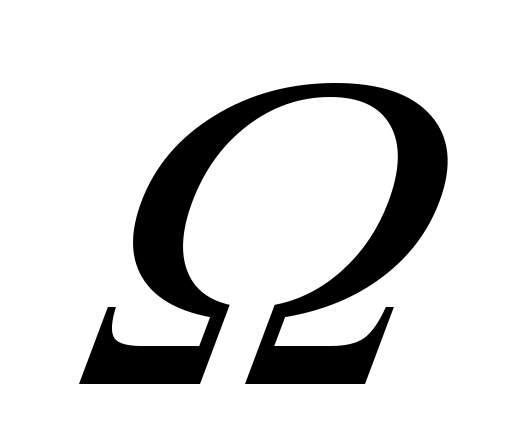 ; дополнительные свойства функции выбора, которые позволяют сузить множество возможных функций выбора ; дополнительные свойства функции выбора, которые позволяют сузить множество возможных функций выбора 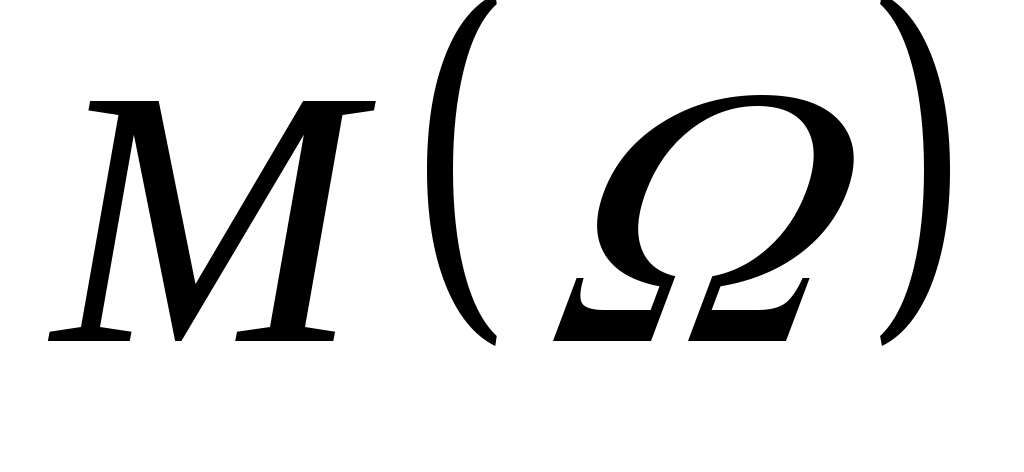 до до 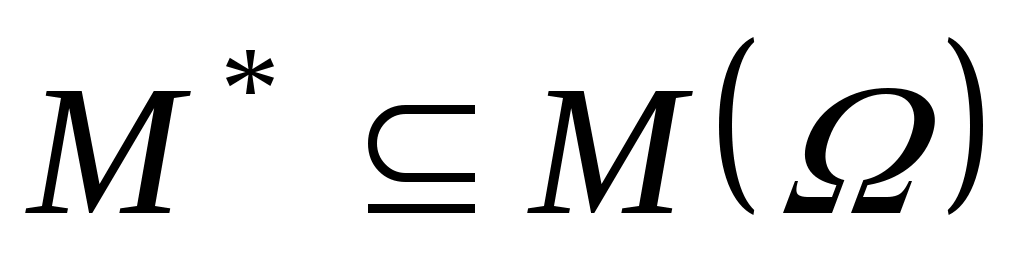 ; ; 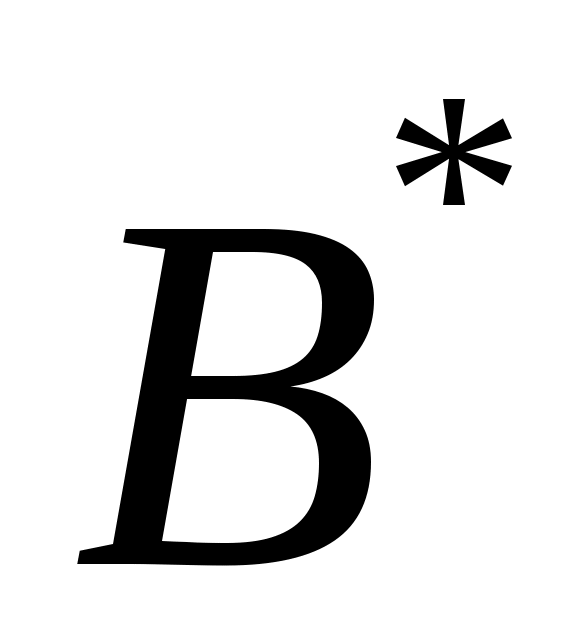 – множество тех подмножеств множества – множество тех подмножеств множества 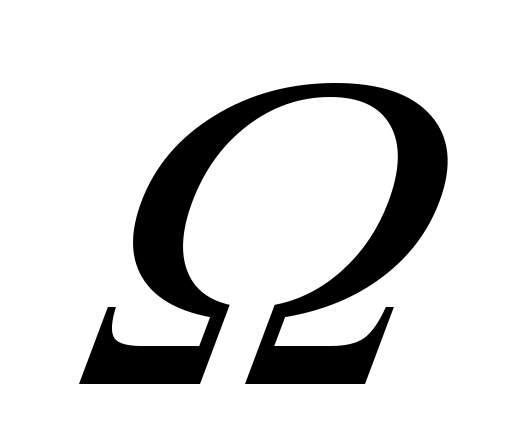 , на которых известны значения функции выбора ( , на которых известны значения функции выбора (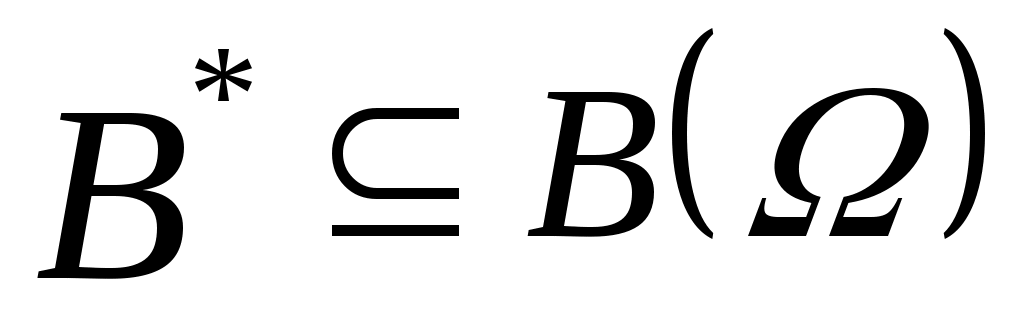 , где , где 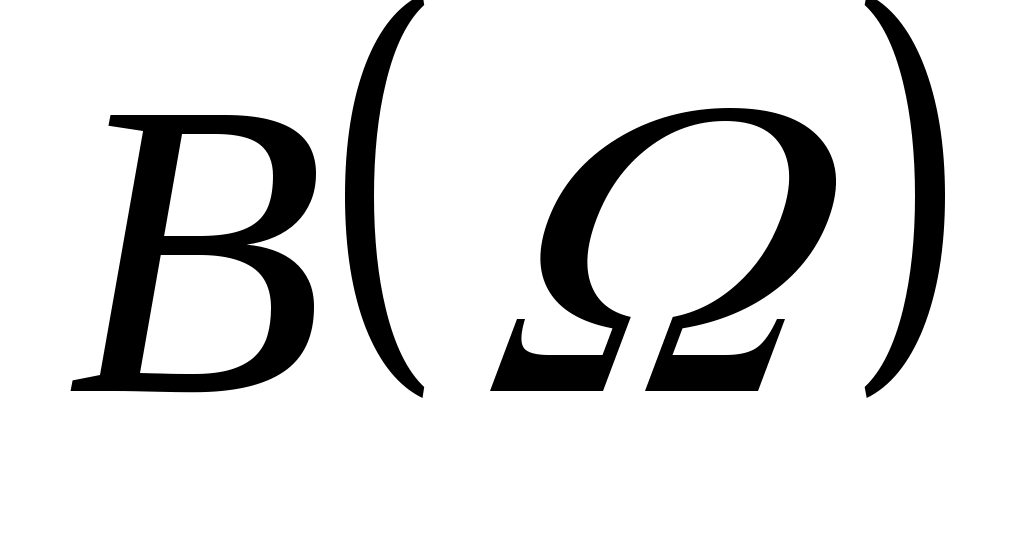 – множество подмножеств – множество подмножеств 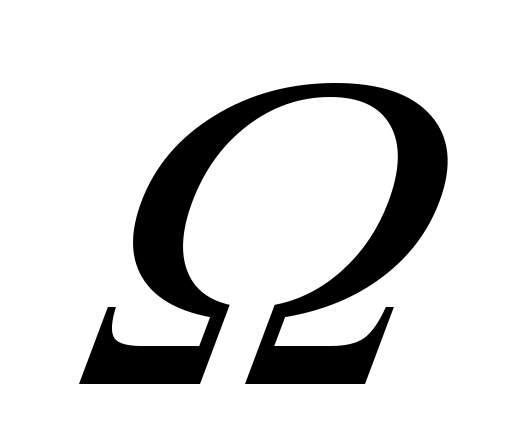 ). Пара ). Пара 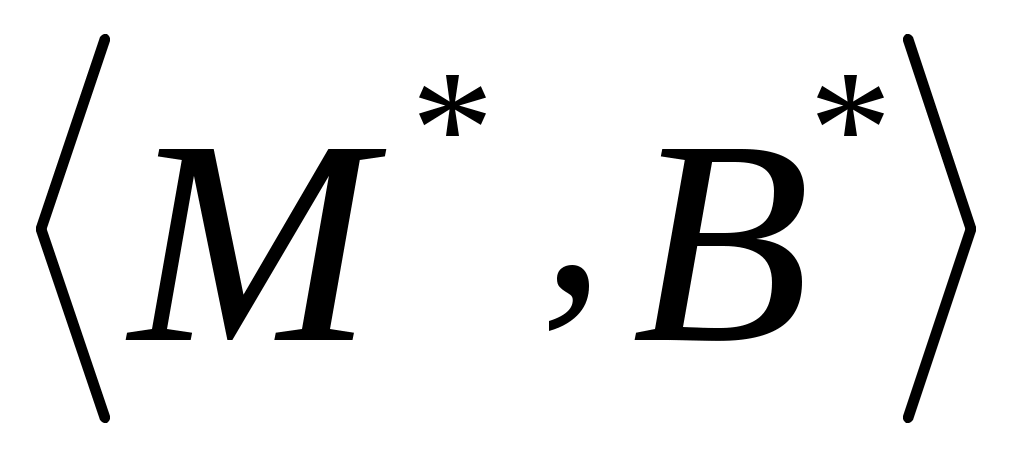 задает описание функции С. Причем, случай задает описание функции С. Причем, случай 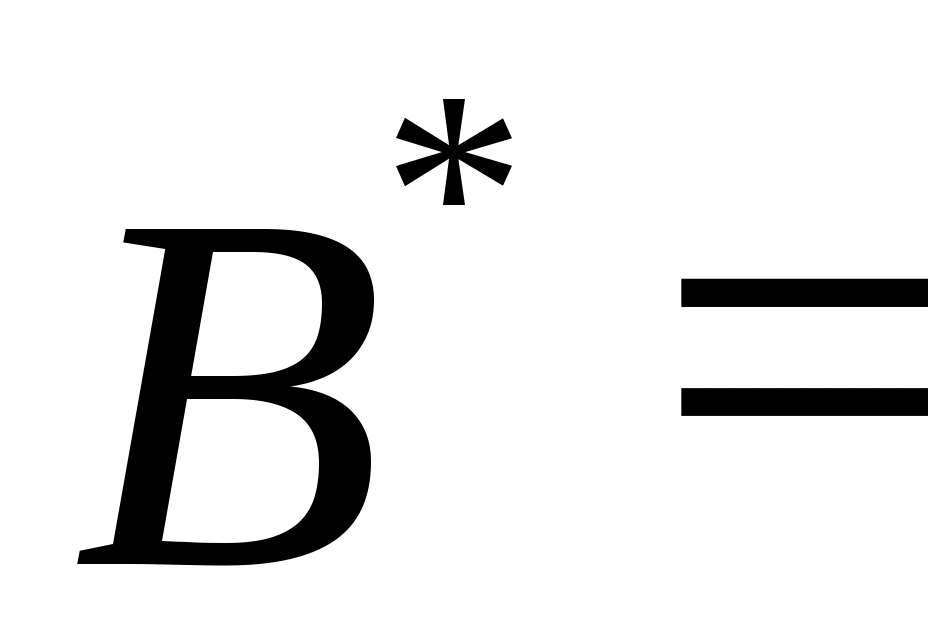 и и 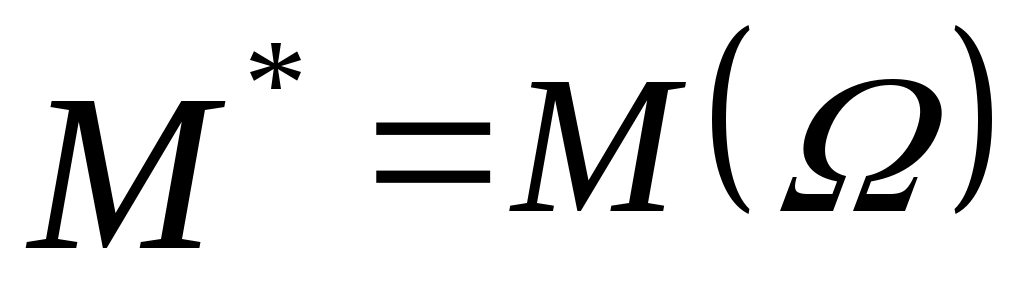 соответствует отсутствию информации о функции С, случай соответствует отсутствию информации о функции С, случай 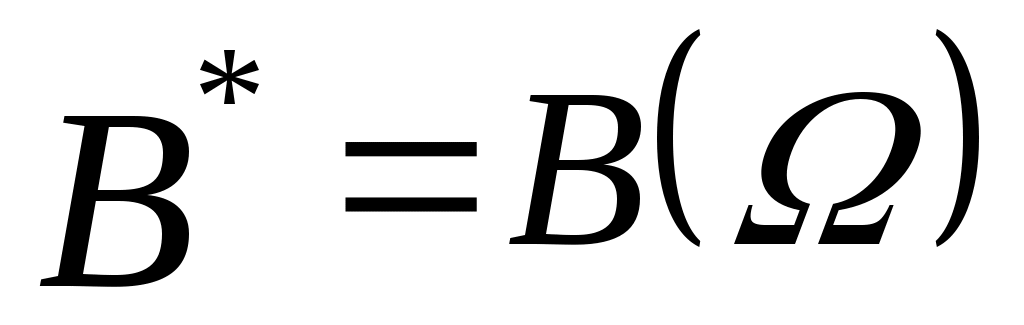 соответствует полному описанию функции. соответствует полному описанию функции.
Математической задачей выбора назовем тройку 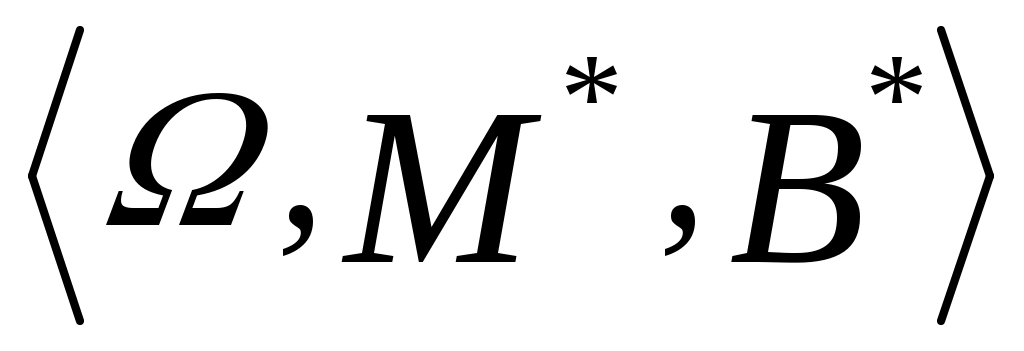 , где , где 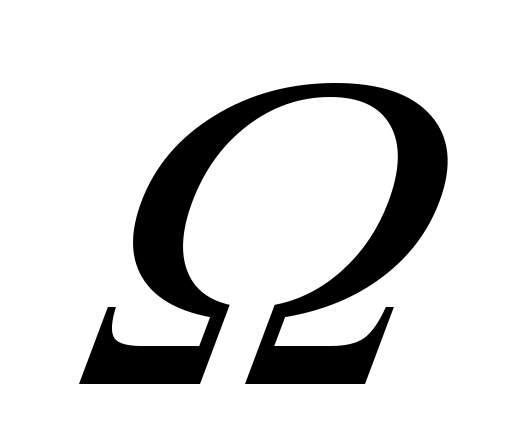 – множество альтернатив; – множество альтернатив; 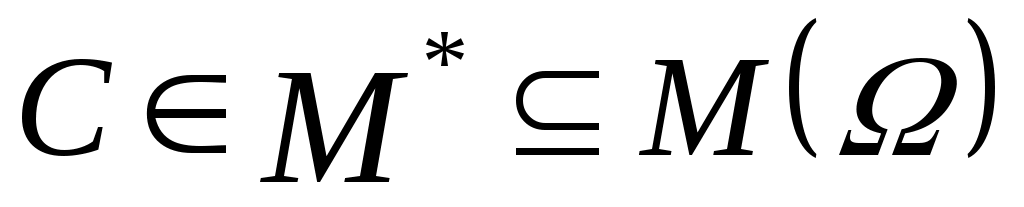 ; ; 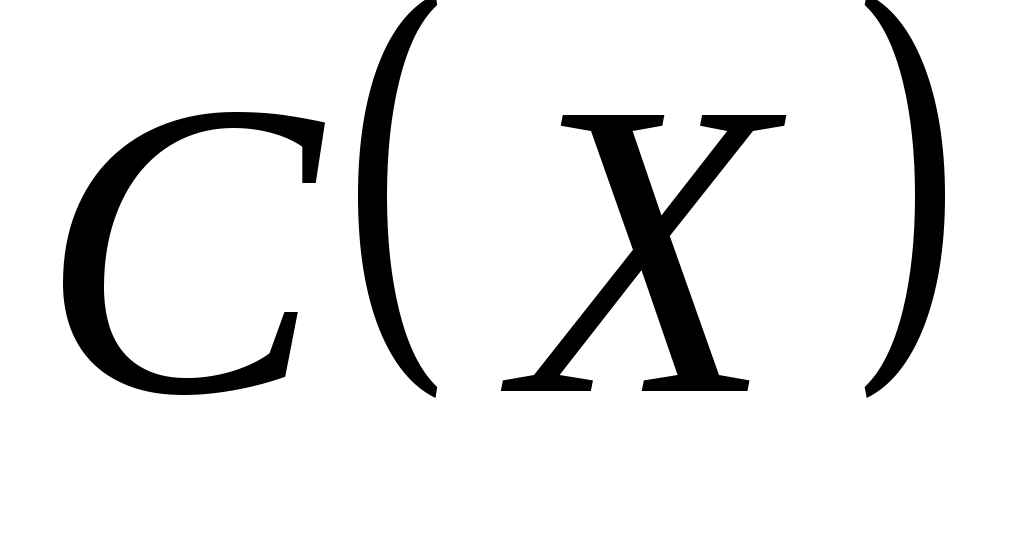 известны для всех известны для всех 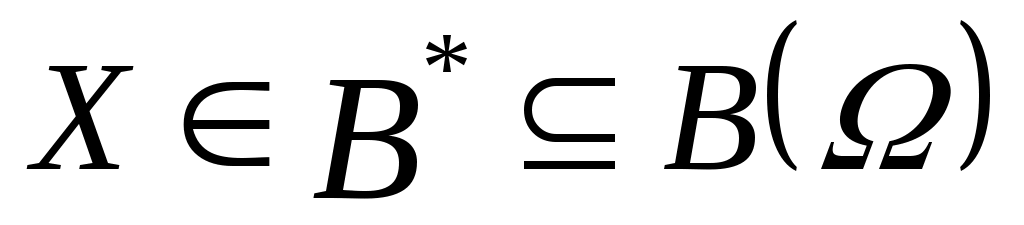 . .
Решением задачи 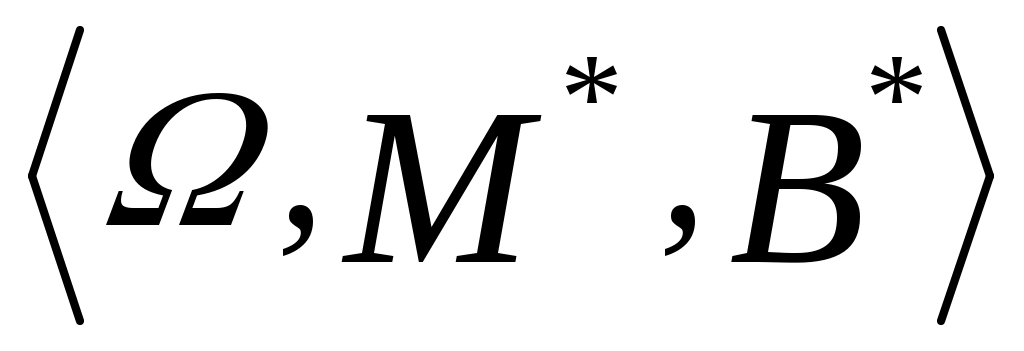 является множество является множество 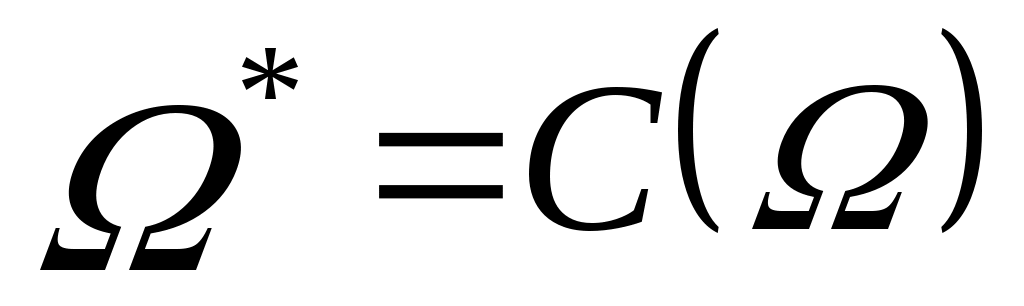 . Задача разрешима, если . Задача разрешима, если 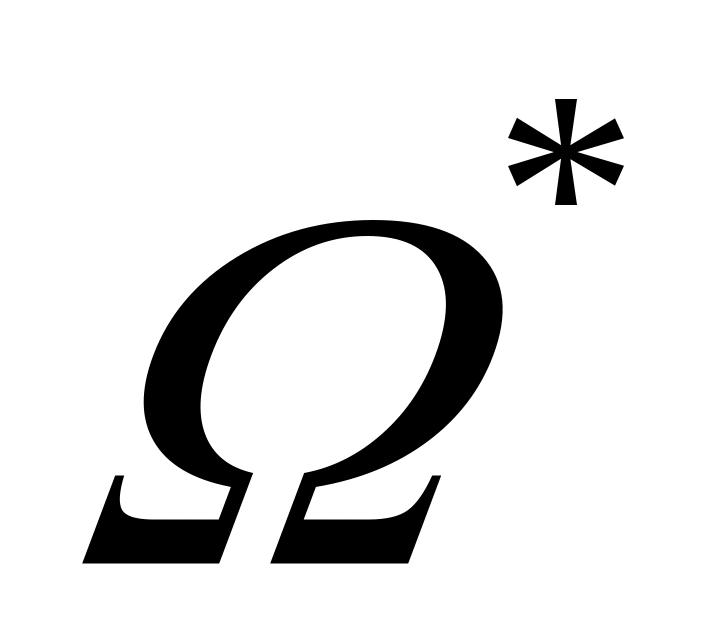 однозначно определяется по множеству однозначно определяется по множеству 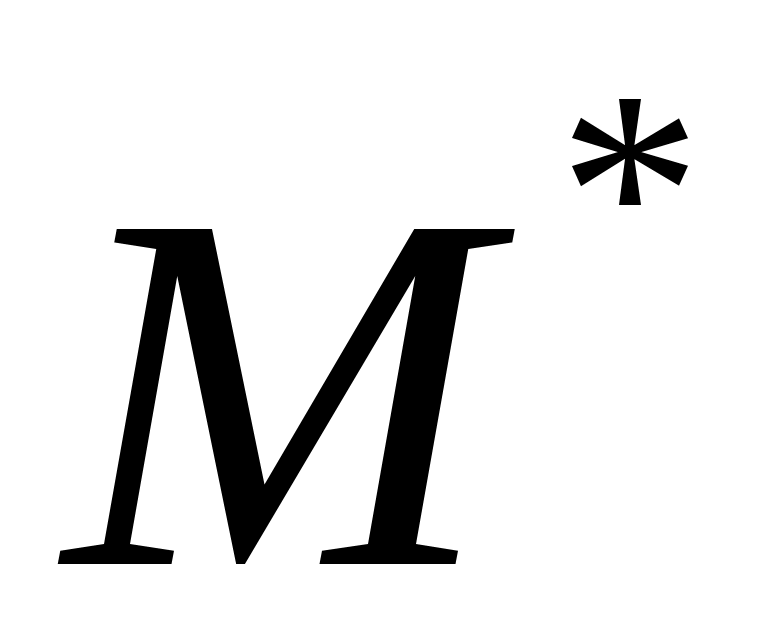 и значениям С на всех и значениям С на всех 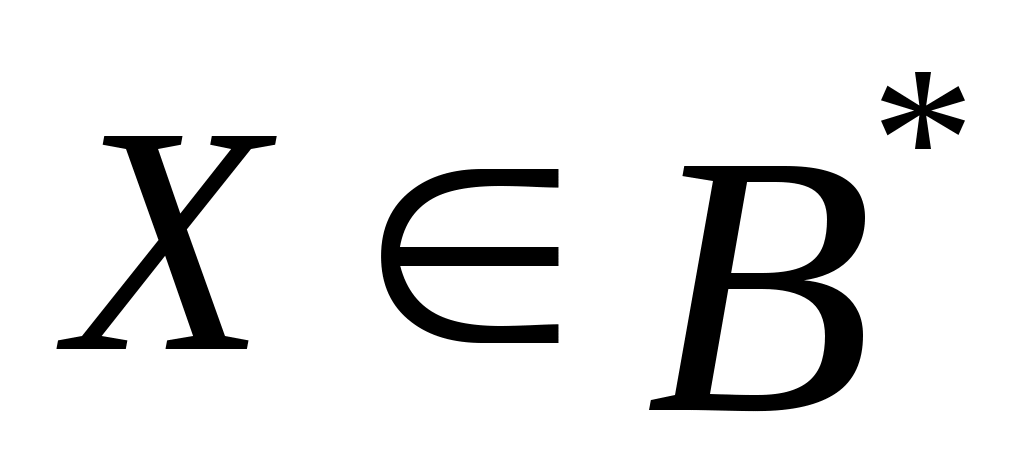 . При . При 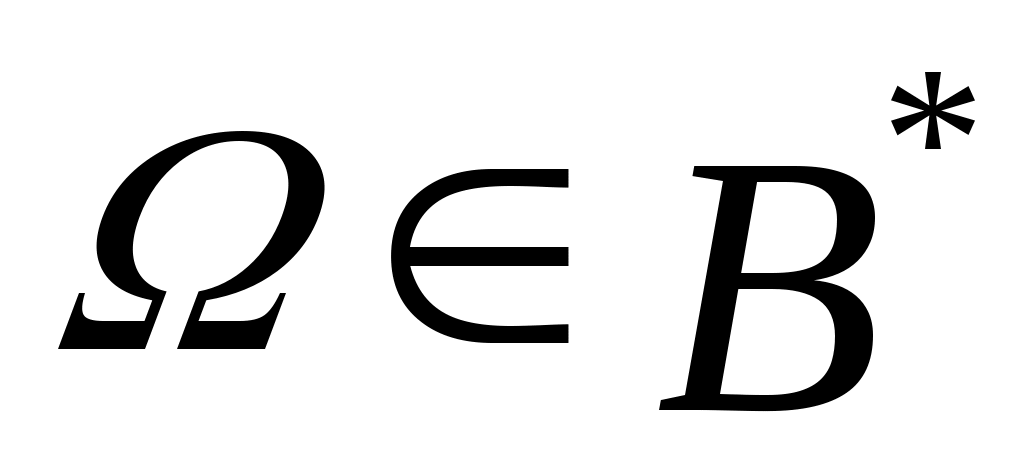 задача разрешима и ее решением является известное задача разрешима и ее решением является известное 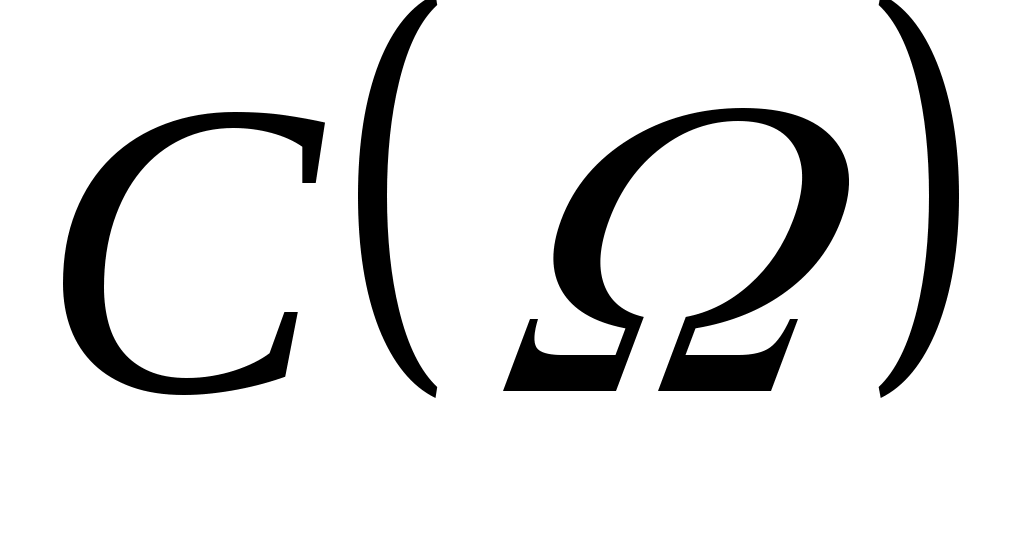 . .
Ведем на множестве 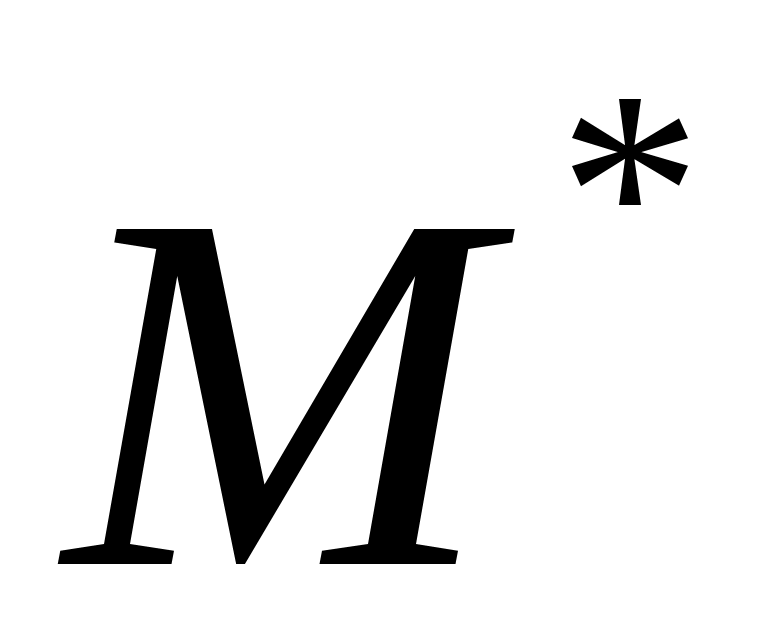 два следующих отношения эквивалентности два следующих отношения эквивалентности 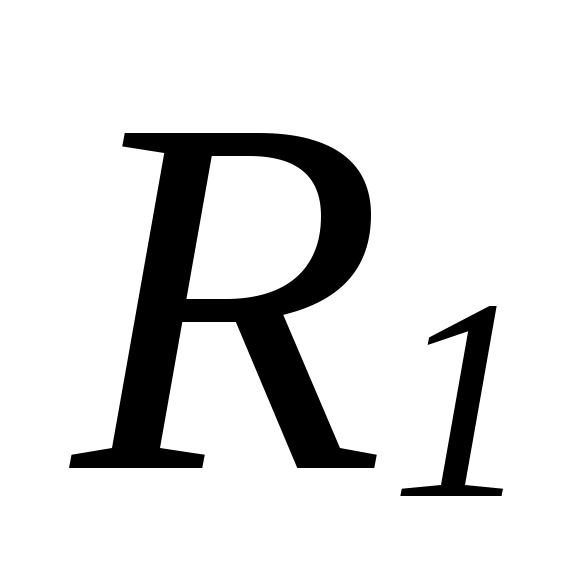 и и 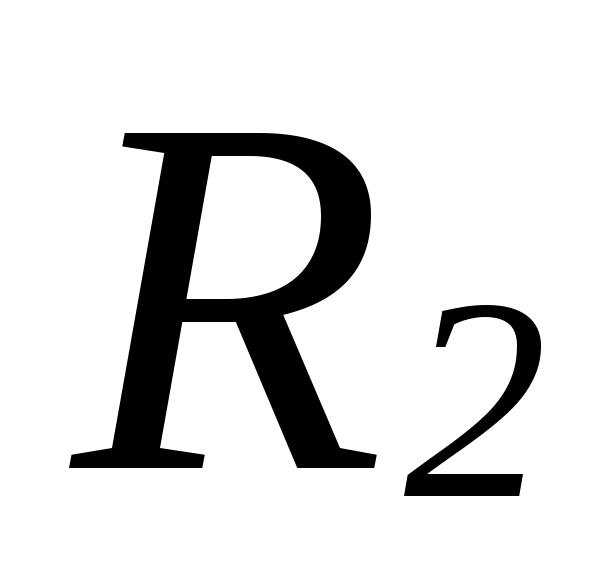 : :
1) 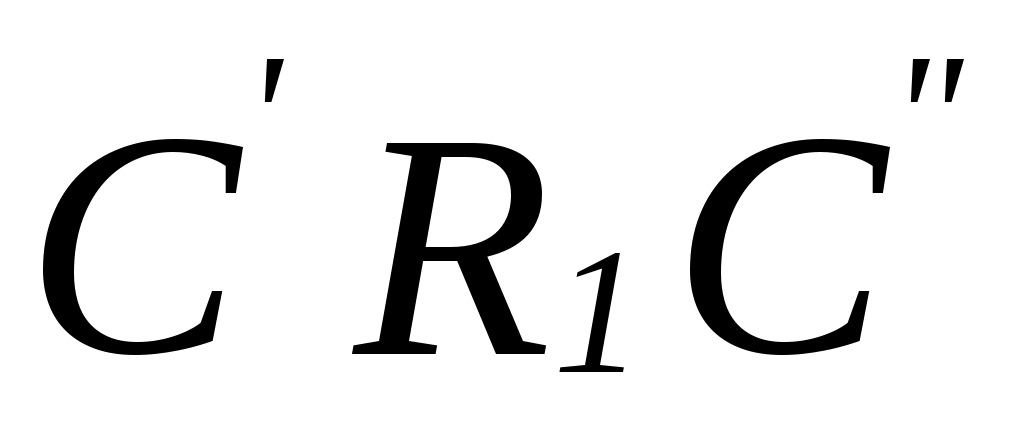  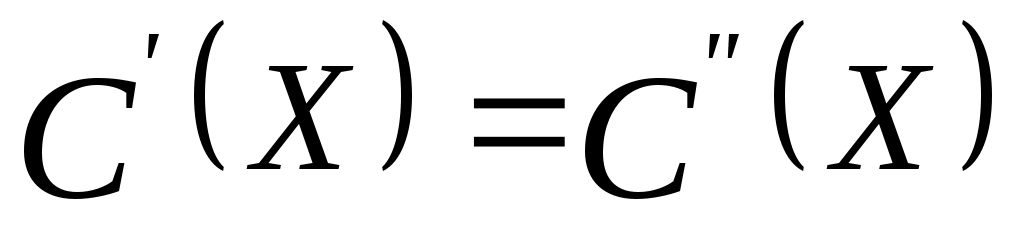 для всех для всех 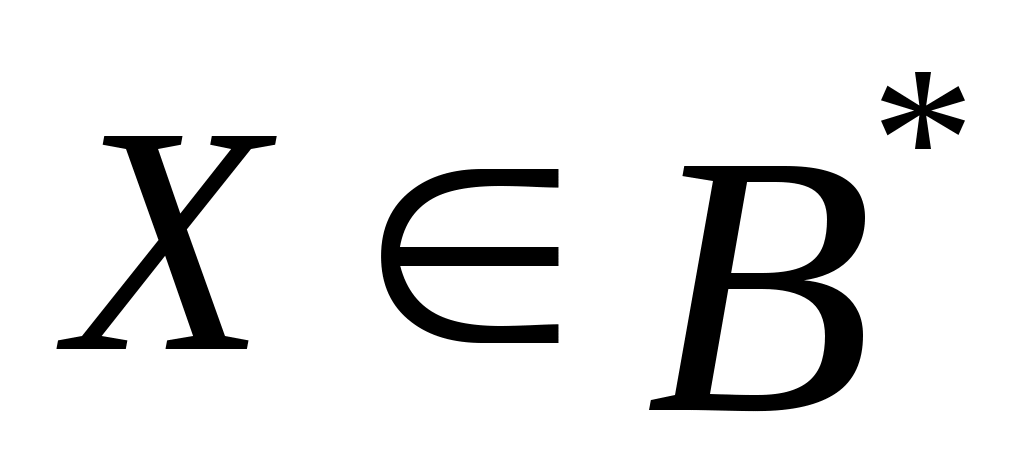 ; ;
2) 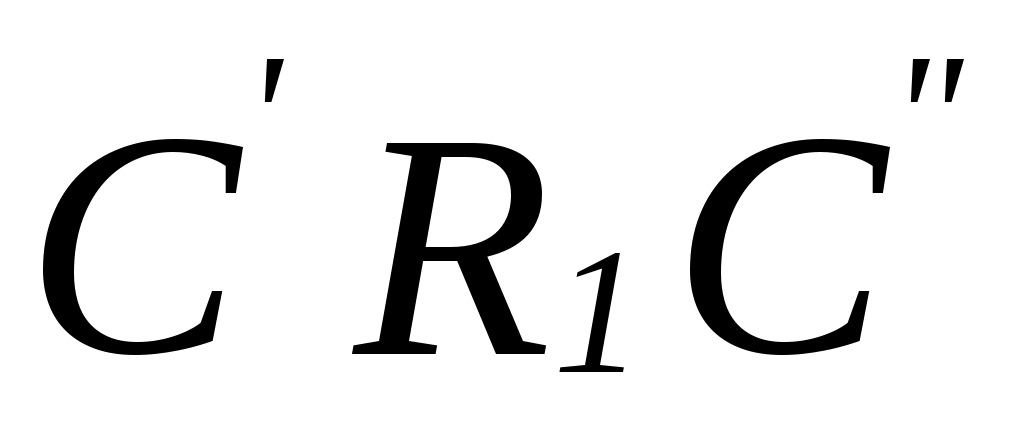  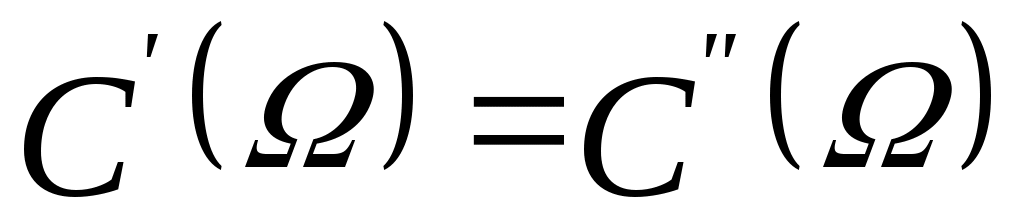 . .
Рассмотрим фактормножества множества 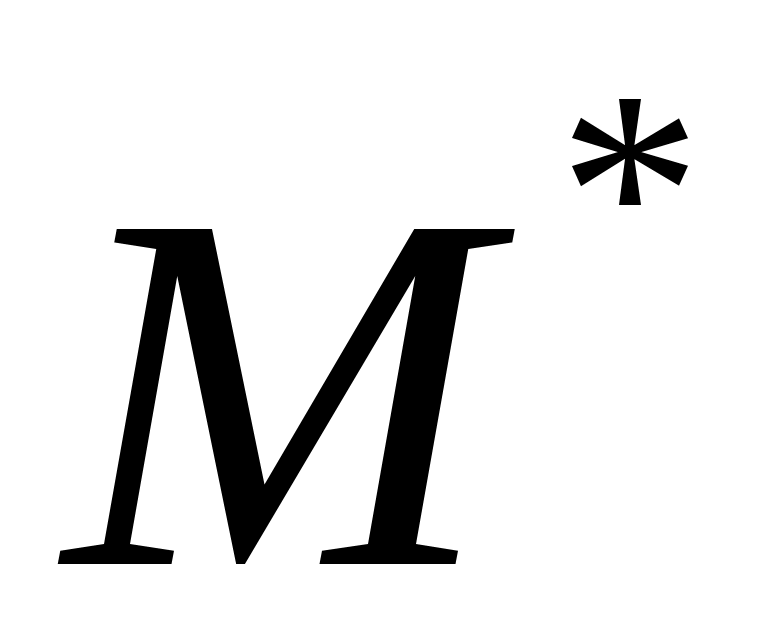 по введенным отношениям: по введенным отношениям:  , , 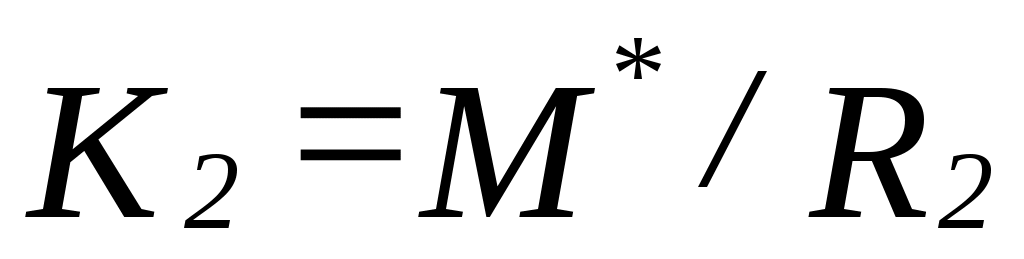 . .
Будем говорить, что фактормножество 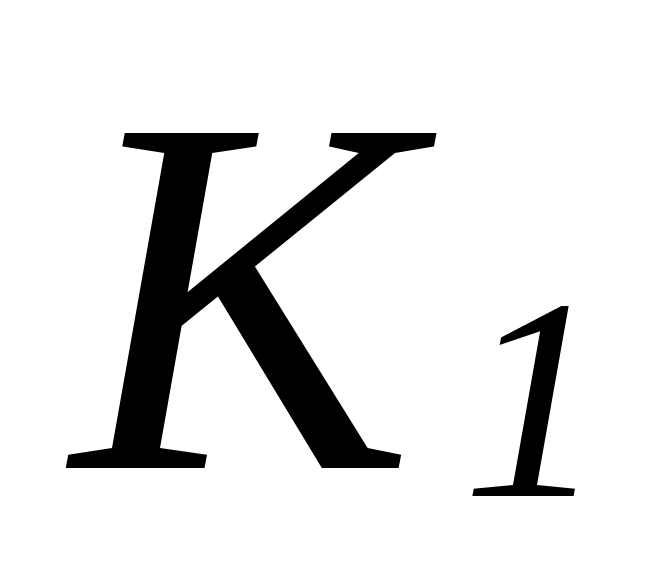 вложено в вложено в 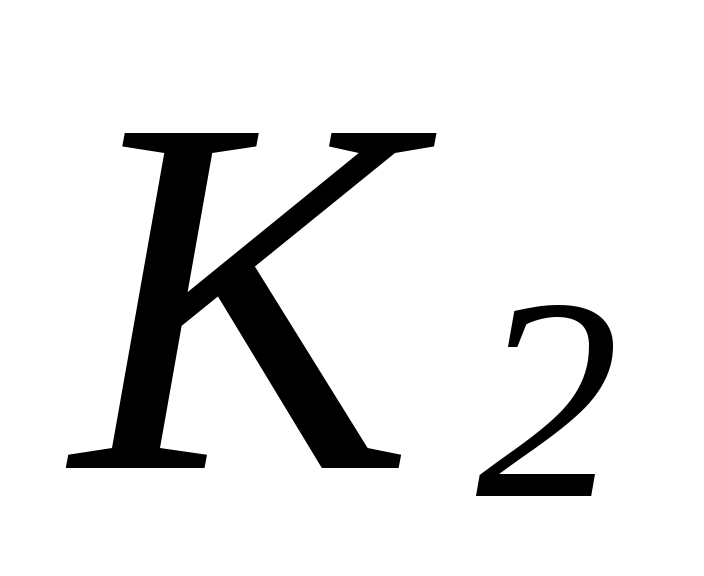 , если для любого класса эквивалентности , если для любого класса эквивалентности 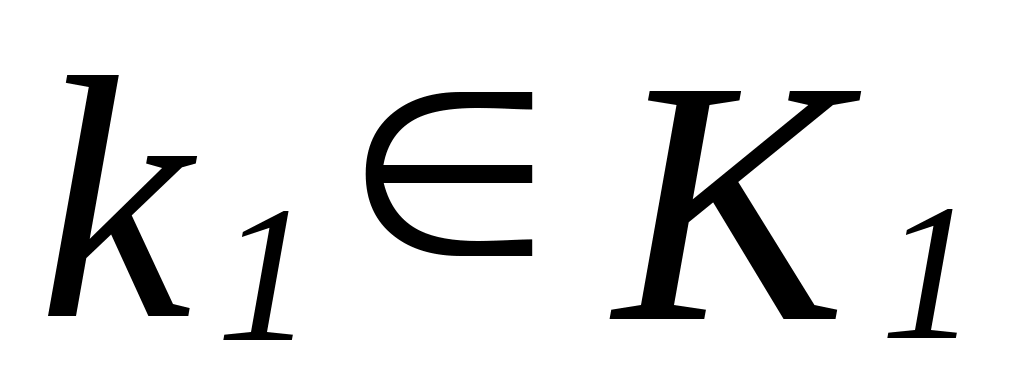 найдется класс эквивалентности найдется класс эквивалентности 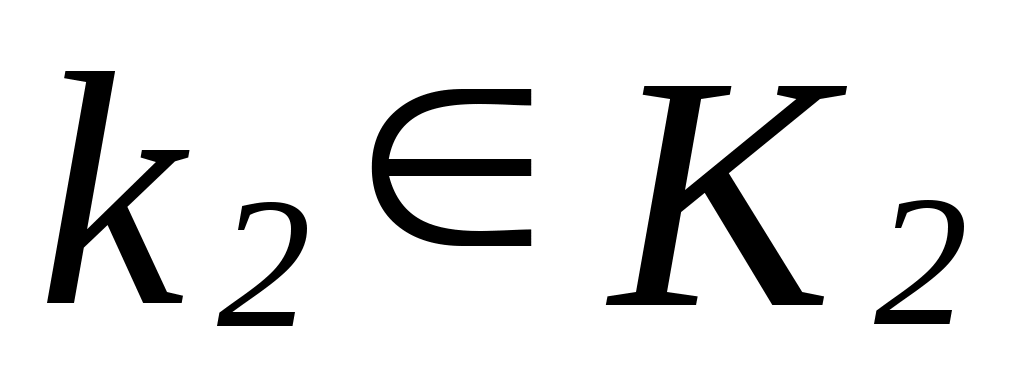 такой, что такой, что  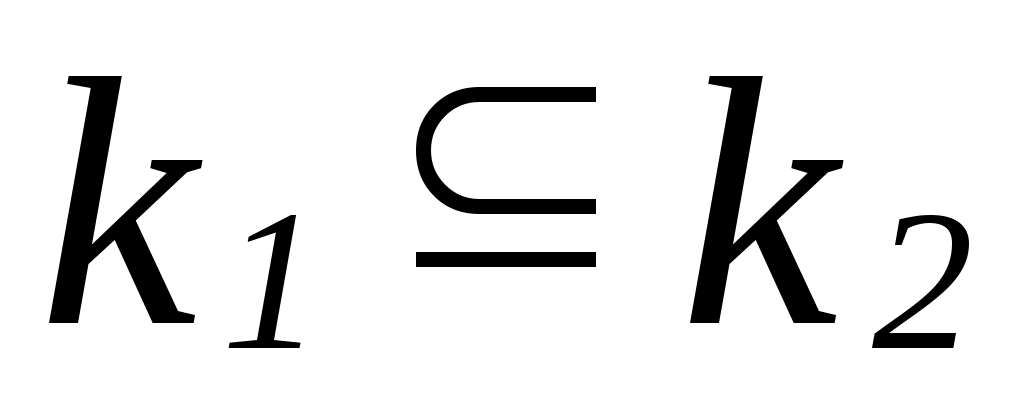 . .
Справедлива следующая теорема.
Теорема 3. Математическая задача выбора 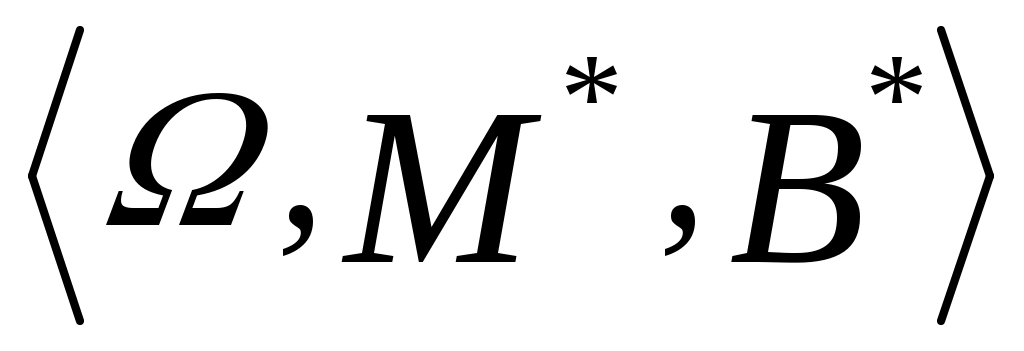 разрешима тогда и только тогда, когда фактормножество разрешима тогда и только тогда, когда фактормножество 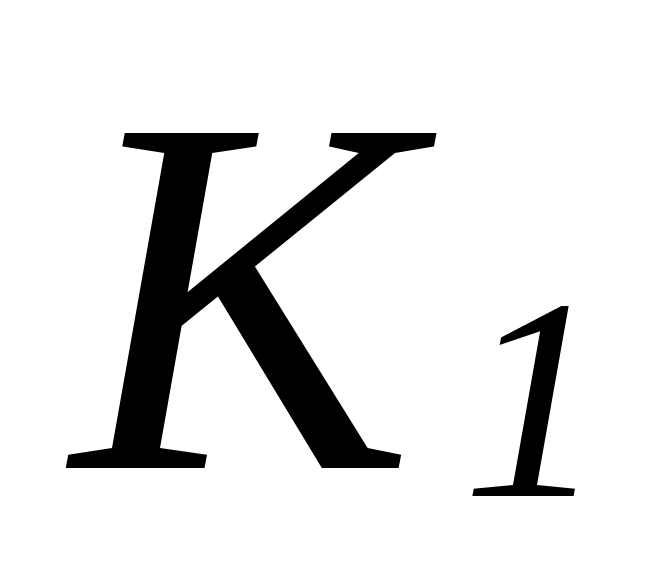 вложено в вложено в 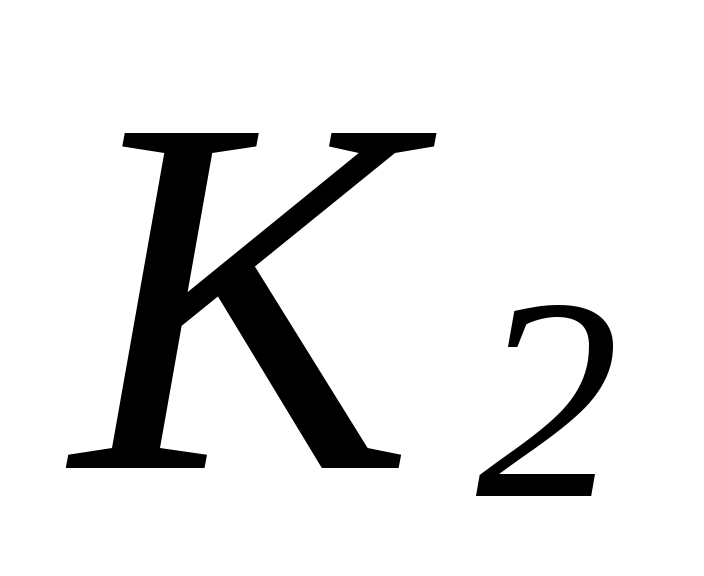 . .
Алгоритм 2 (алгоритм решения математической задачи выбора)
1. Сформировать множество 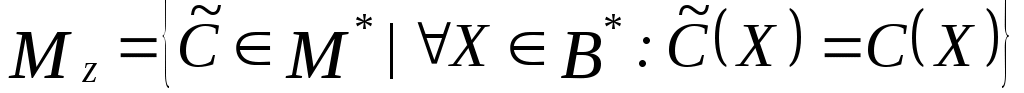 . .
Занумеровать все функции выбора, входящие в 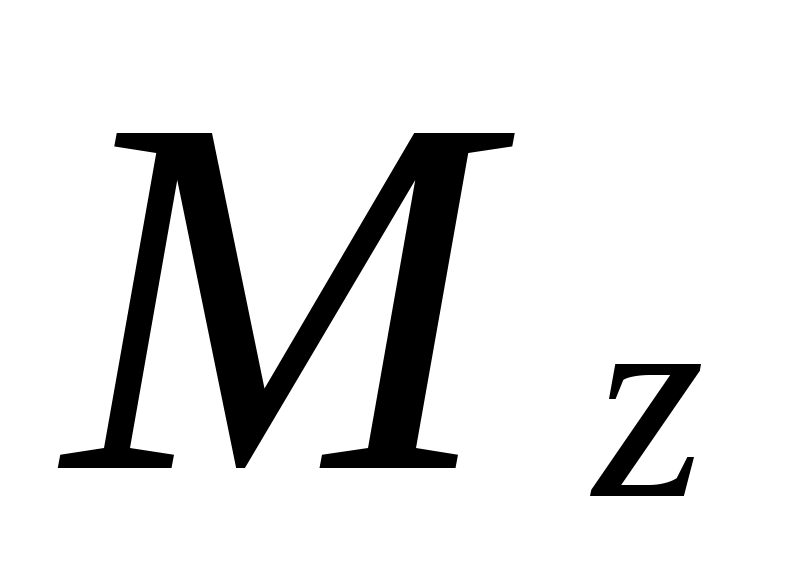 : : 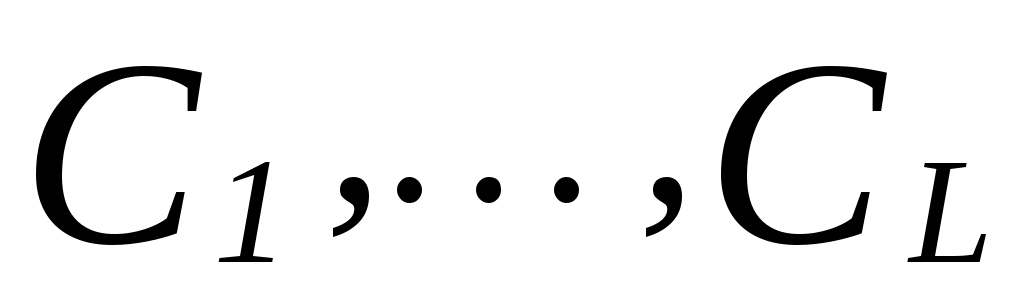 . .
Если 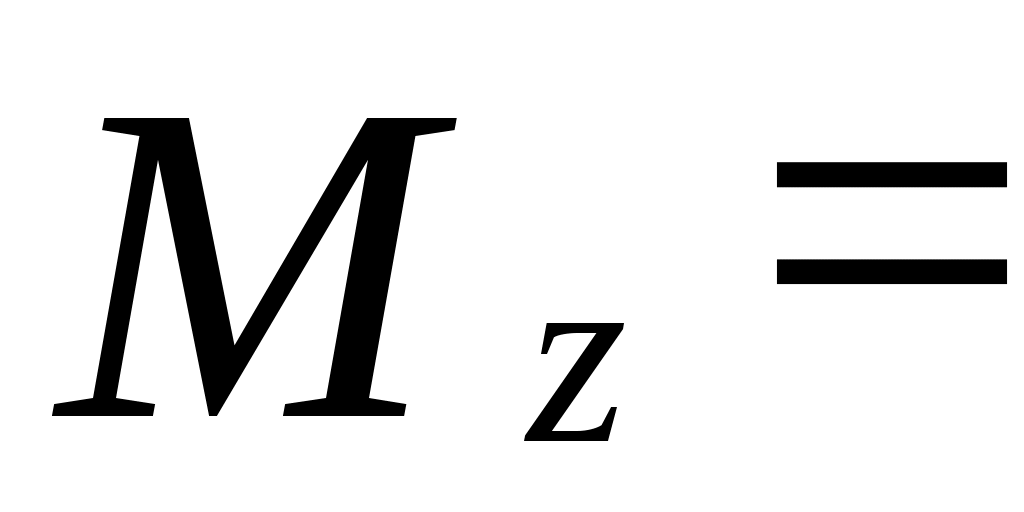 , перейти к шагу 9. Иначе перейти к шагу 4. , перейти к шагу 9. Иначе перейти к шагу 4.
Положить 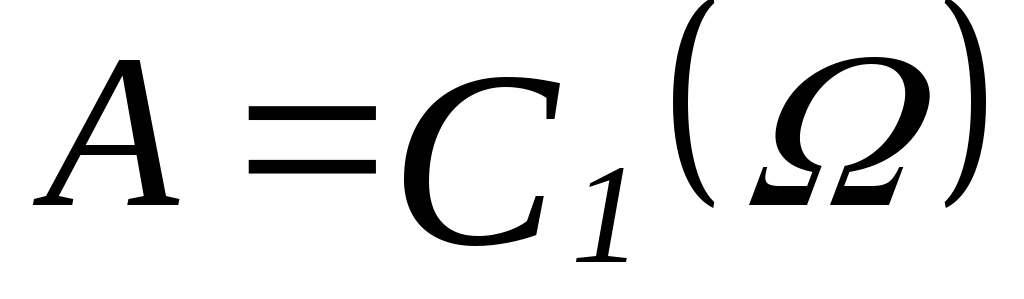 . .
Положить i=2.
Если 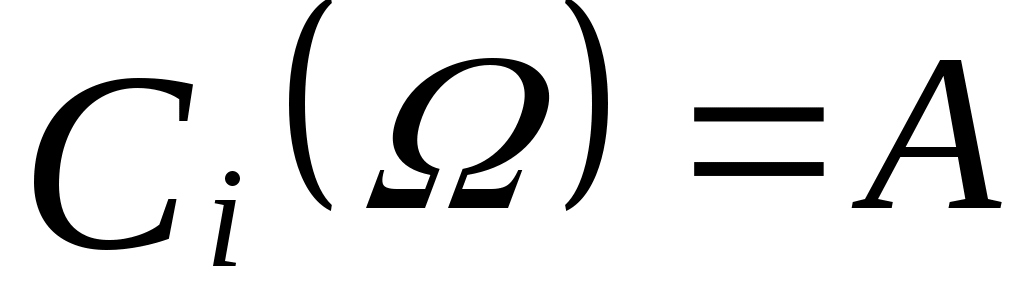 , то перейти к шагу 8. Иначе – к шагу 9. , то перейти к шагу 8. Иначе – к шагу 9.
Если 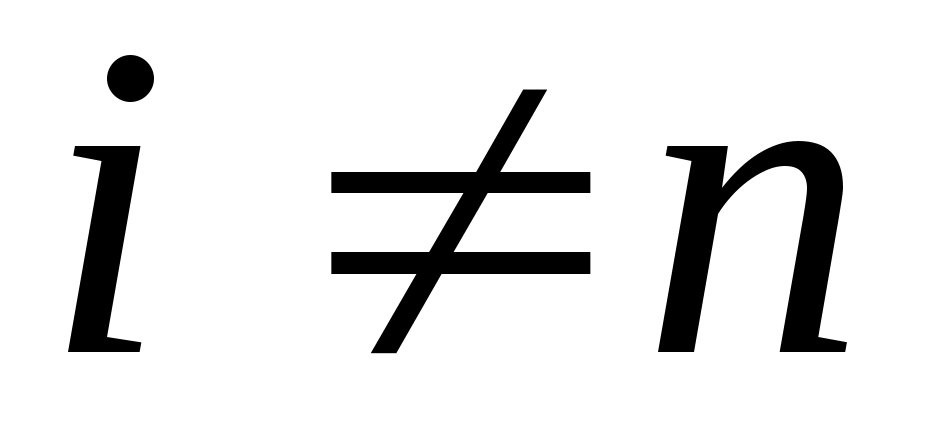 , то , то 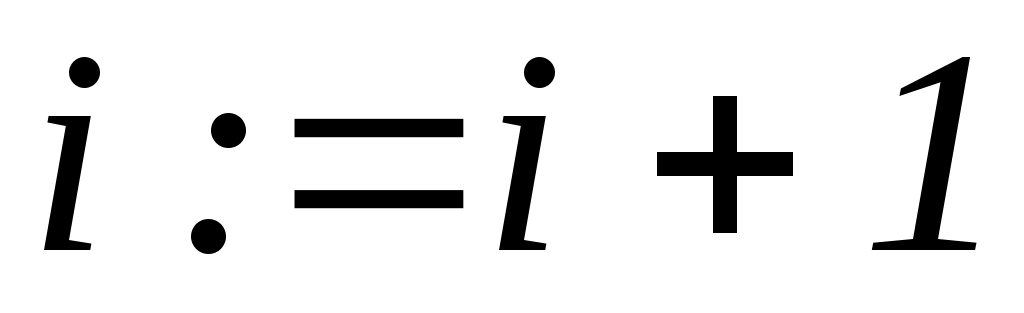 , перейти к шагу 6. Иначе – к шагу 8. , перейти к шагу 6. Иначе – к шагу 8.
Останов. Множество A является решением задачи 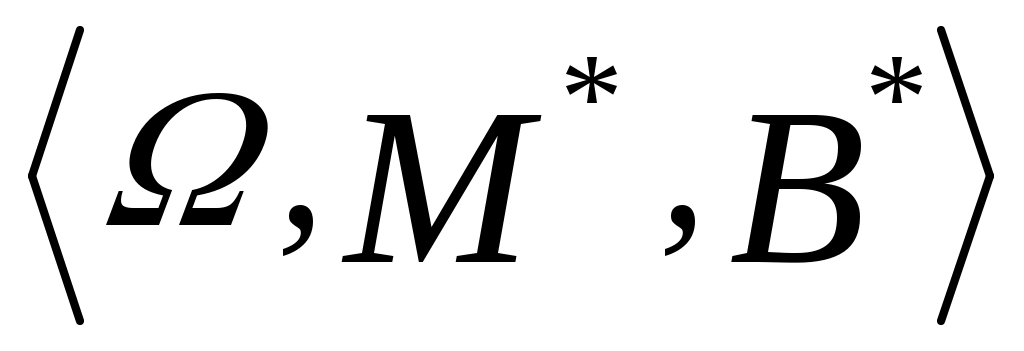 . .
Останов. Задача 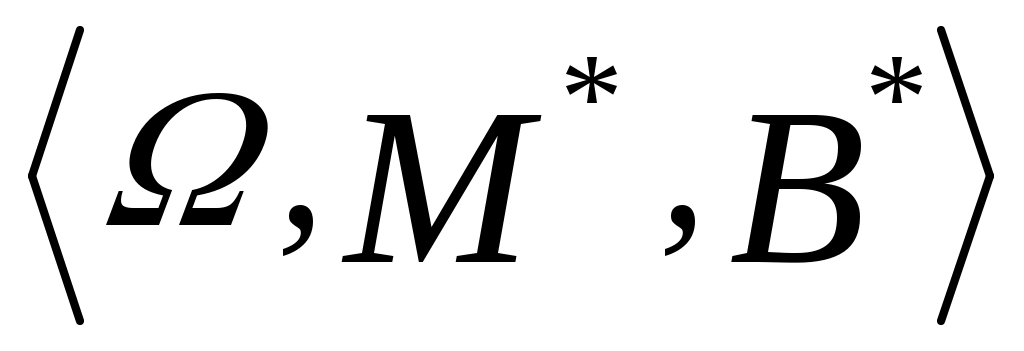 неразрешима. неразрешима.
Задача выбора на основе скалярной и общей скалярной функции выбора
Функция выбора С на 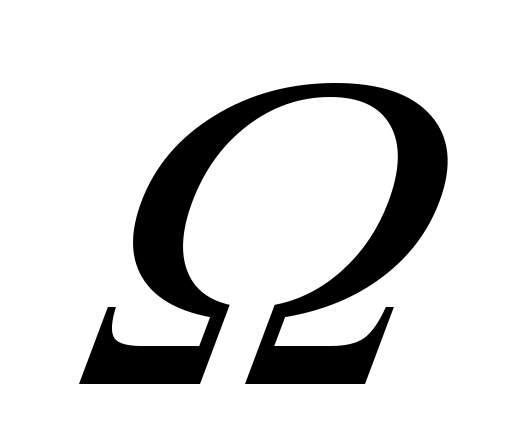 называется общей скалярной функцией, если существует числовая функция называется общей скалярной функцией, если существует числовая функция 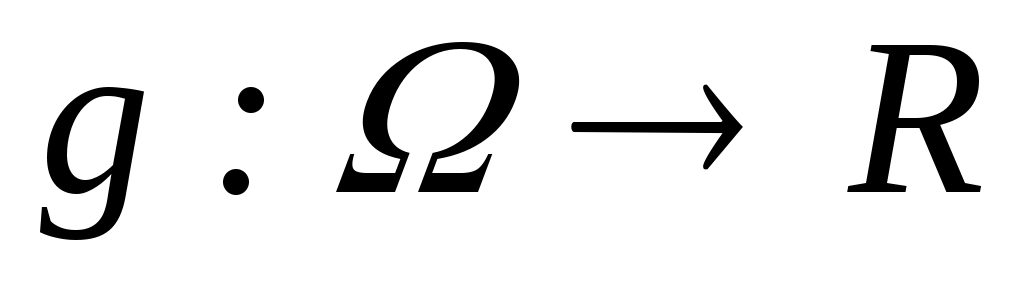 такая, что такая, что 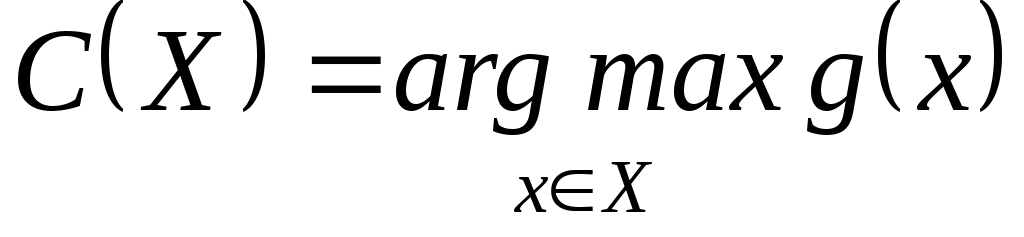 , и скалярной, если , и скалярной, если 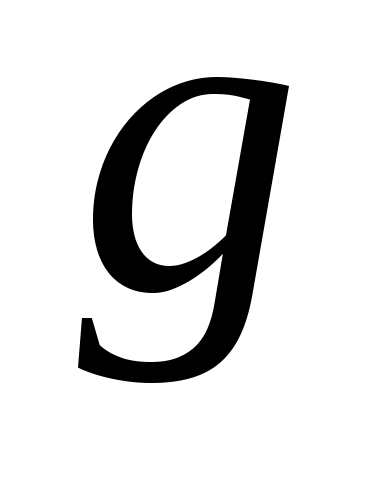 – инъективная функция, т.е. – инъективная функция, т.е. 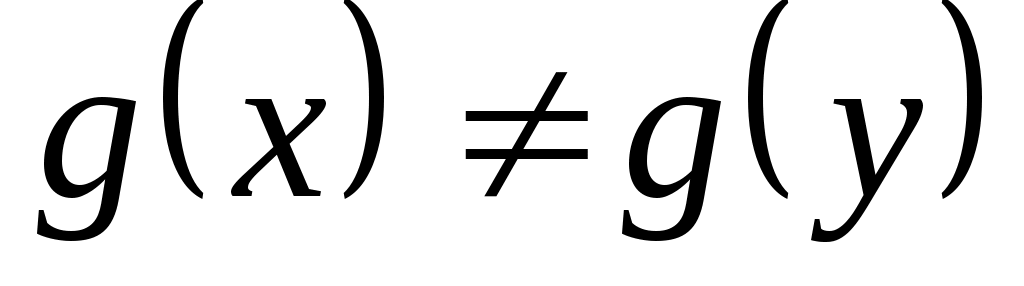 при при 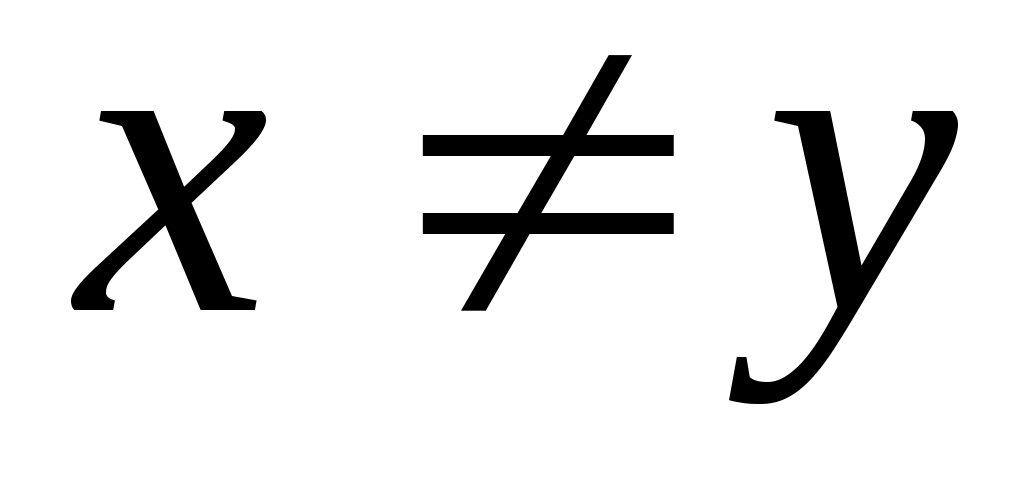 . .
Функция выбора С является общей скалярной функцией тогда и только тогда, когда она порождена сильно транзитивным антирефлексивным бинарным отношением.
Заметим, что функция 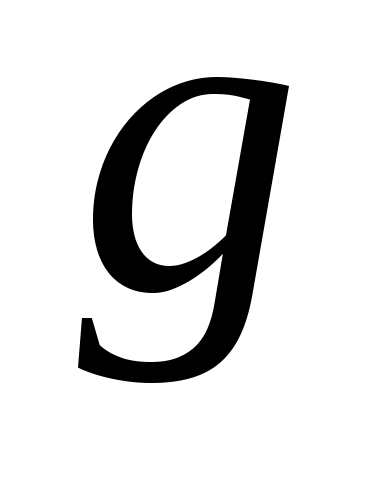 , участвующая в определении общей скалярной и скалярной функции определена с точностью до строго положительного монотонного преобразования. Другими словами, если , участвующая в определении общей скалярной и скалярной функции определена с точностью до строго положительного монотонного преобразования. Другими словами, если 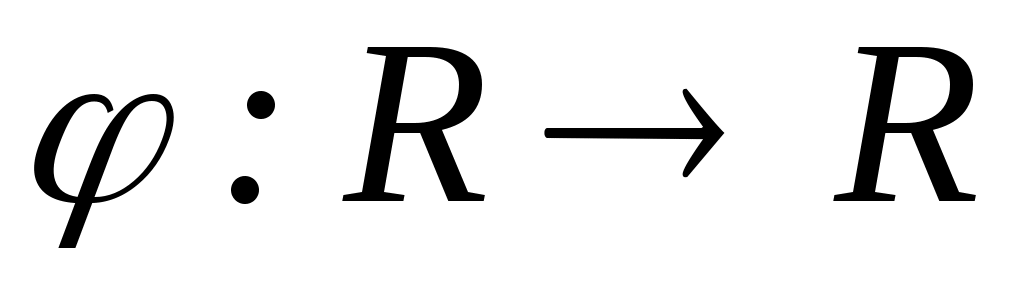 – монотонно возрастающая функция и – монотонно возрастающая функция и 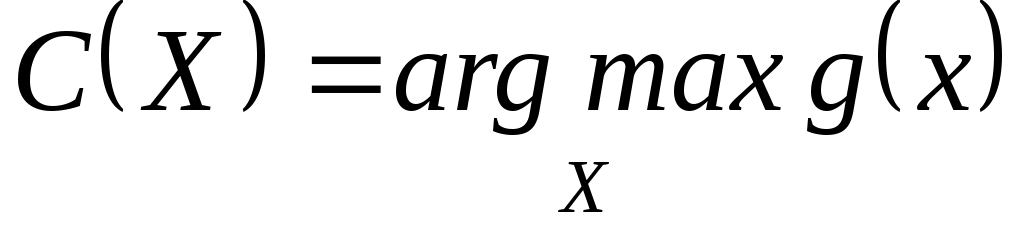 , , 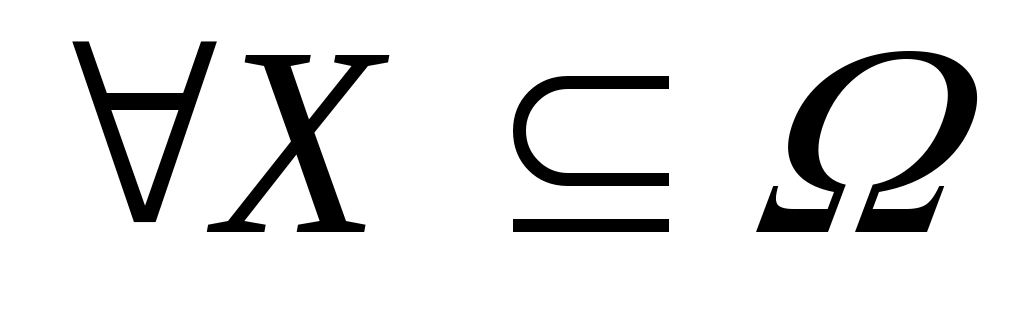 , то , то 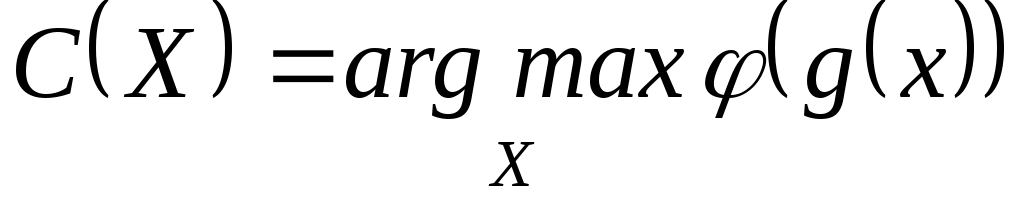 , , 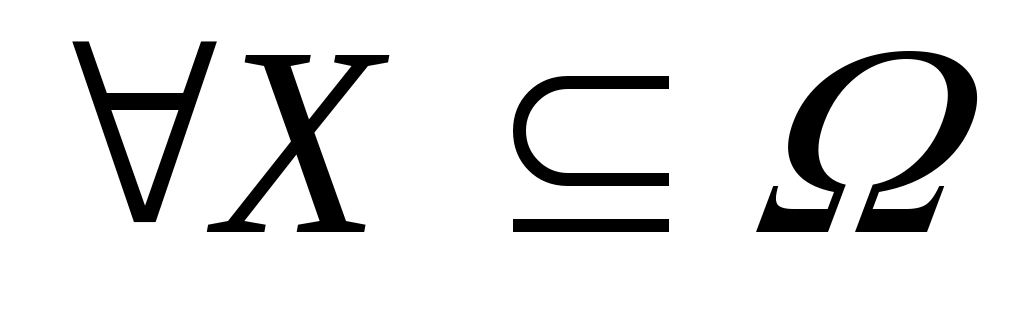 . .
Введем бинарное отношение 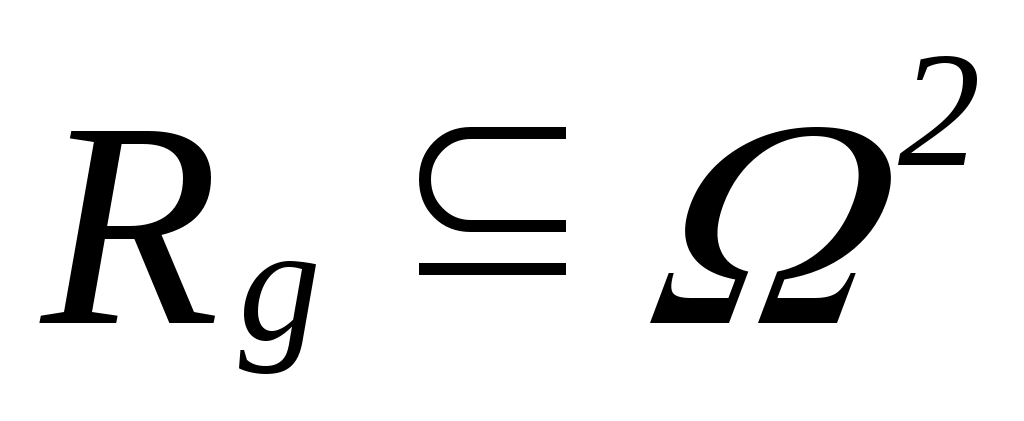 : : 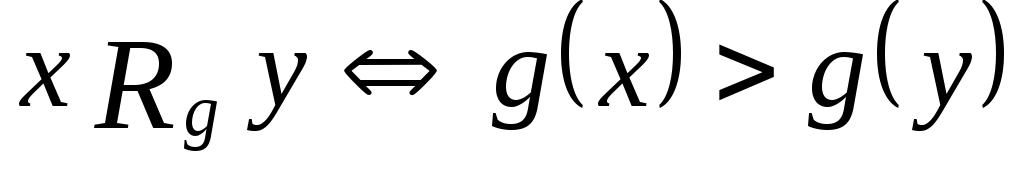 . .
Утверждение 1. Скалярная функция выбора совпадает с предпочтением по бинарному отношению  . .
Докажем справедливость утверждения, т.е. что выполнено равенство: 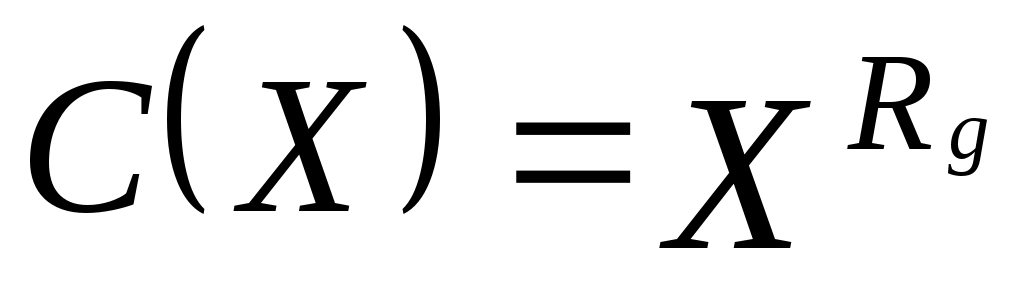 , , 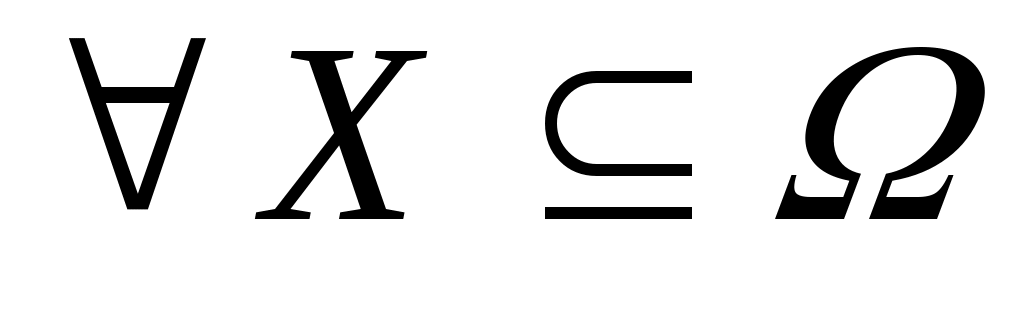 , где , где 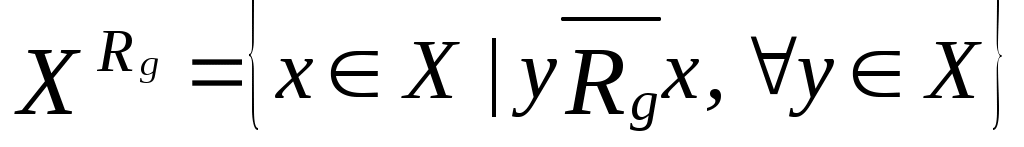 . ………………. . ……………….
Итак, пусть рассмотрим произвольное подмножество 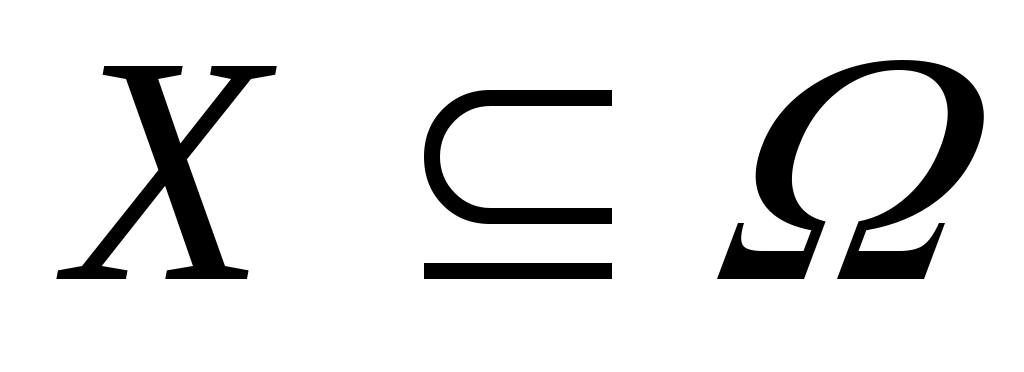 . Докажем, что . Докажем, что 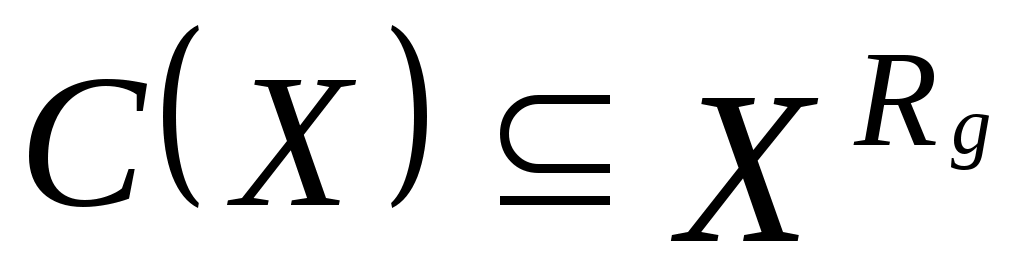 Пусть Пусть 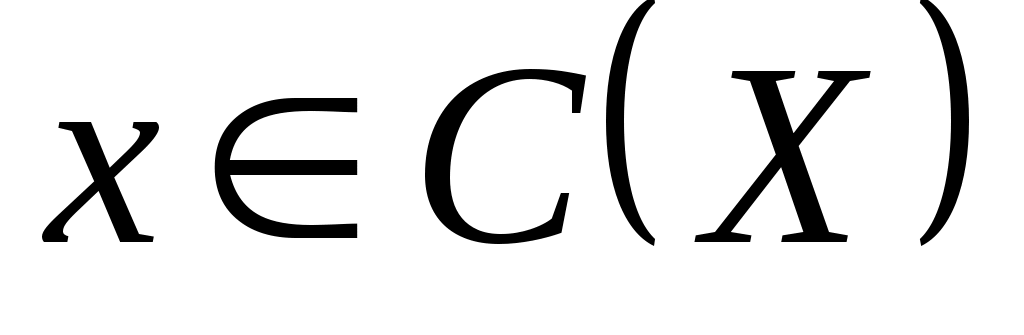 = =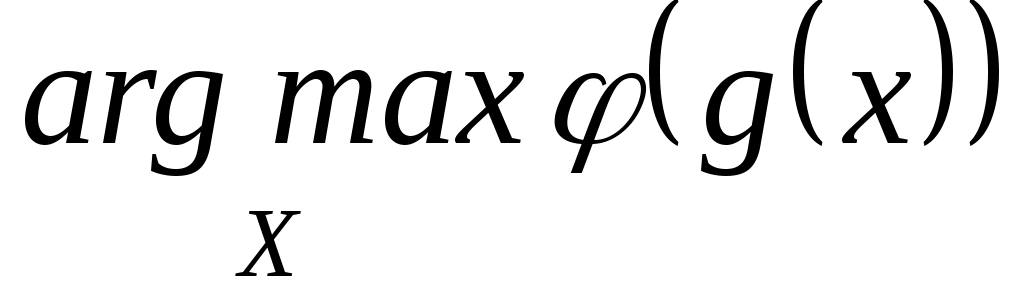 . Тогда . Тогда 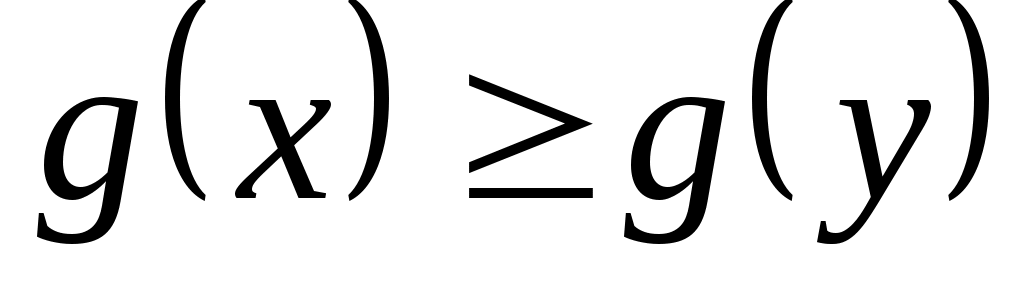 для любого для любого 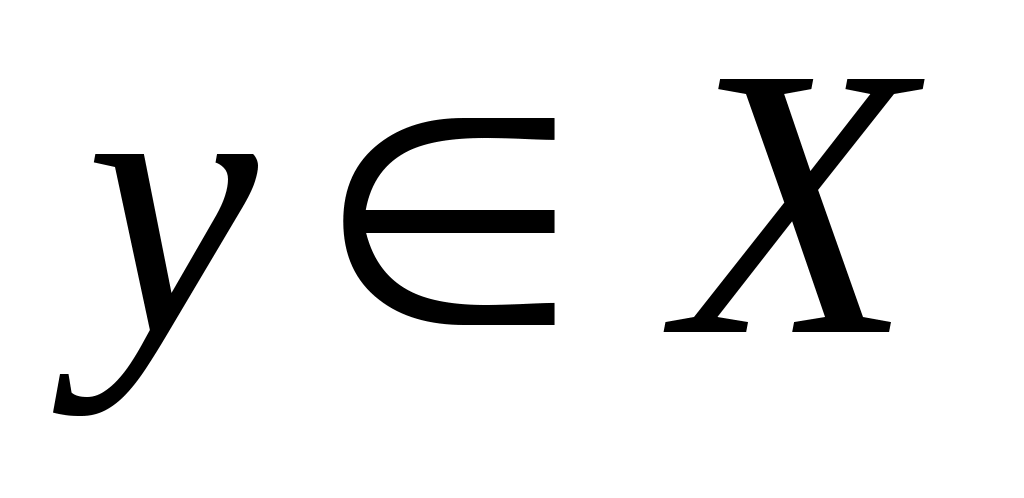 . А следовательно, . А следовательно, 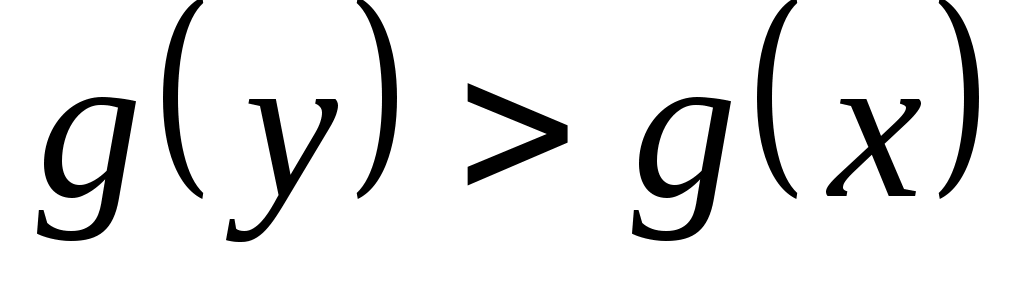 не выполнено, тогда не выполнено, тогда 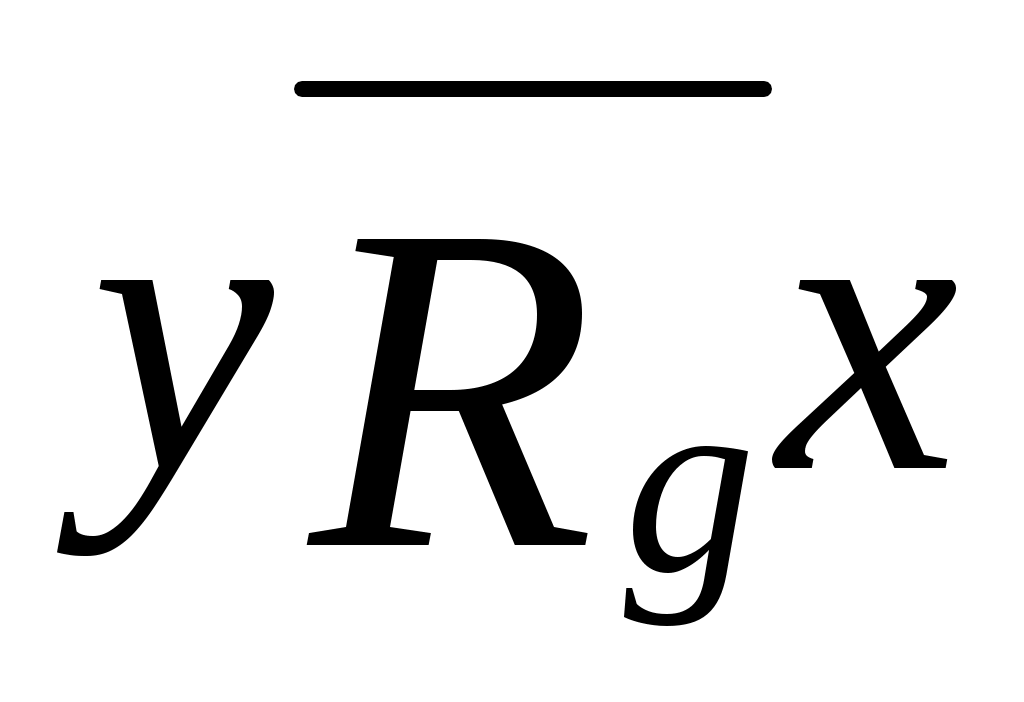 , т.е. , т.е. 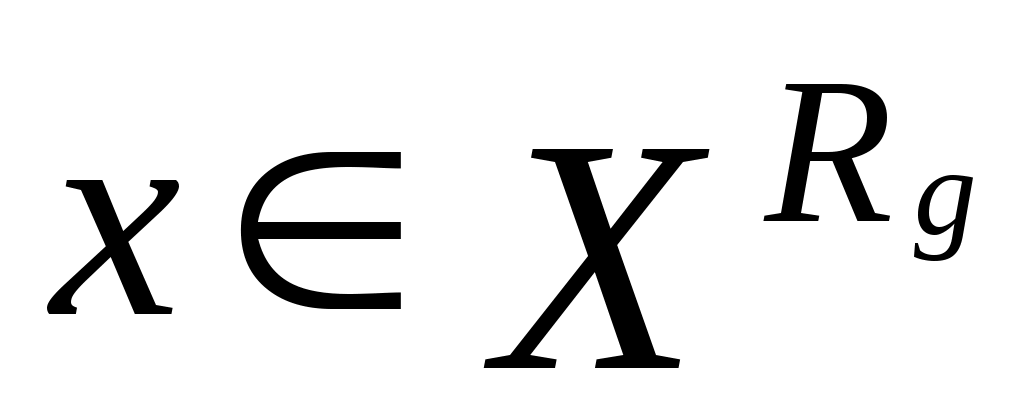 . .
Обратное включение множеств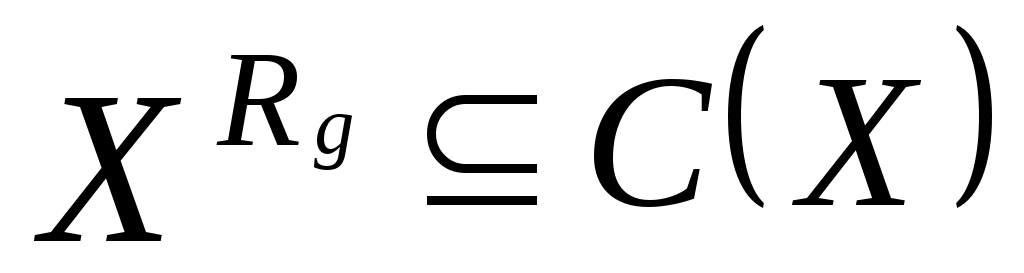 доказывается аналогично. доказывается аналогично.
Таким образом, если 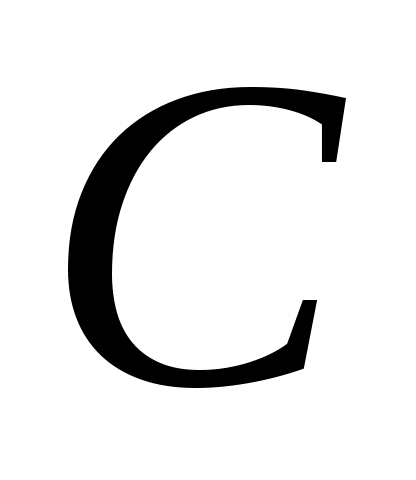 – скалярная функция, то задача выбора сводится к отысканию – скалярная функция, то задача выбора сводится к отысканию
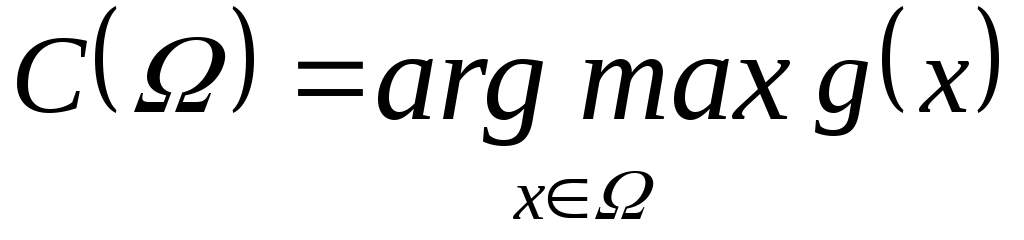 . (4) . (4)
Однако чаще функция 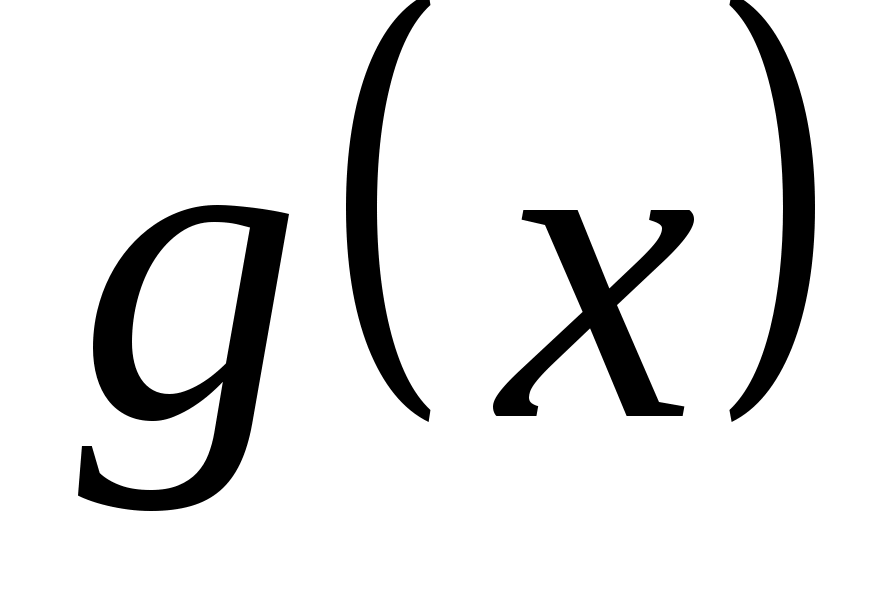 в явном виде не задана. В силу утверждения 1 в этом случае задача (4) является математической задачей выбора, в которой в явном виде не задана. В силу утверждения 1 в этом случае задача (4) является математической задачей выбора, в которой 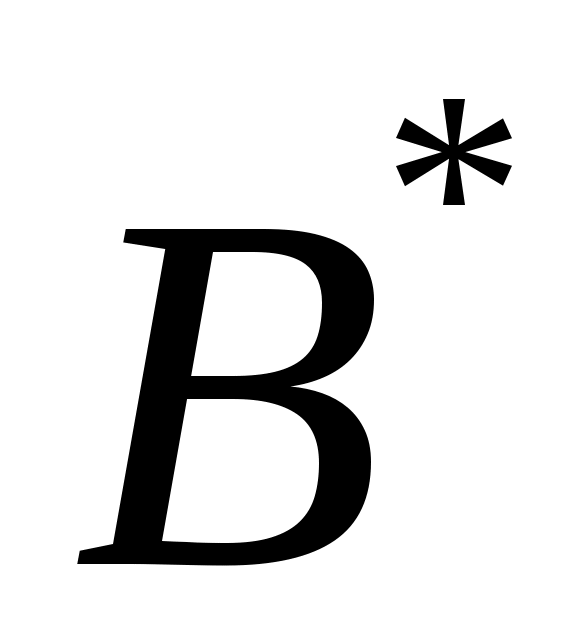 состоит из некоторых двухэлементных подмножеств, а состоит из некоторых двухэлементных подмножеств, а 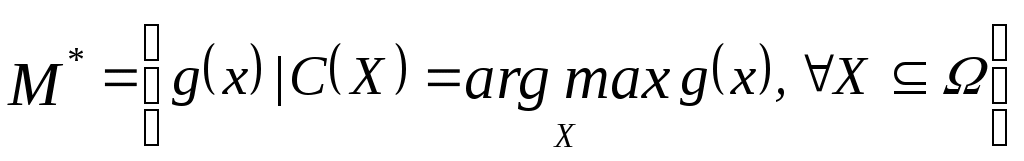 . .
Упражнения к § 4
Основные упражнения
1. Рассмотрим задачу выбора, в которой 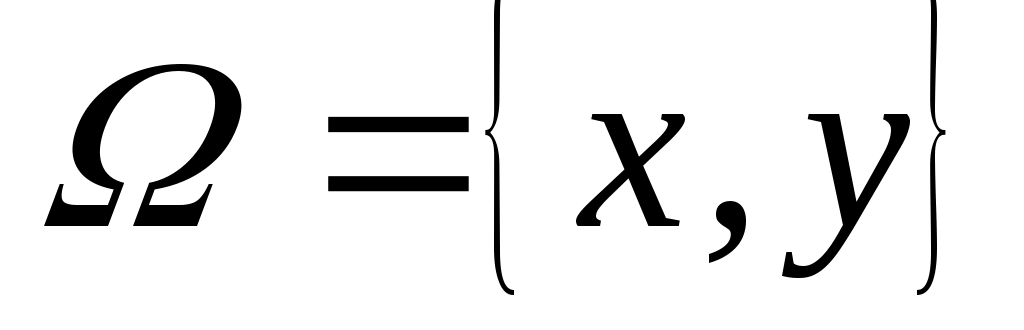 . Известно, что . Известно, что 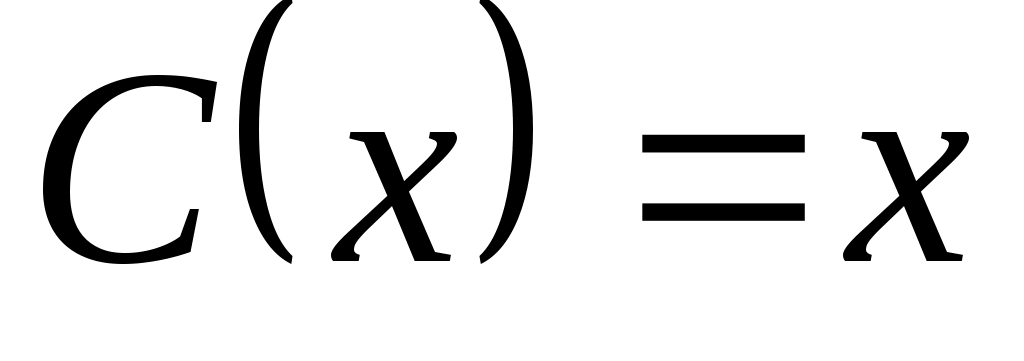 , , 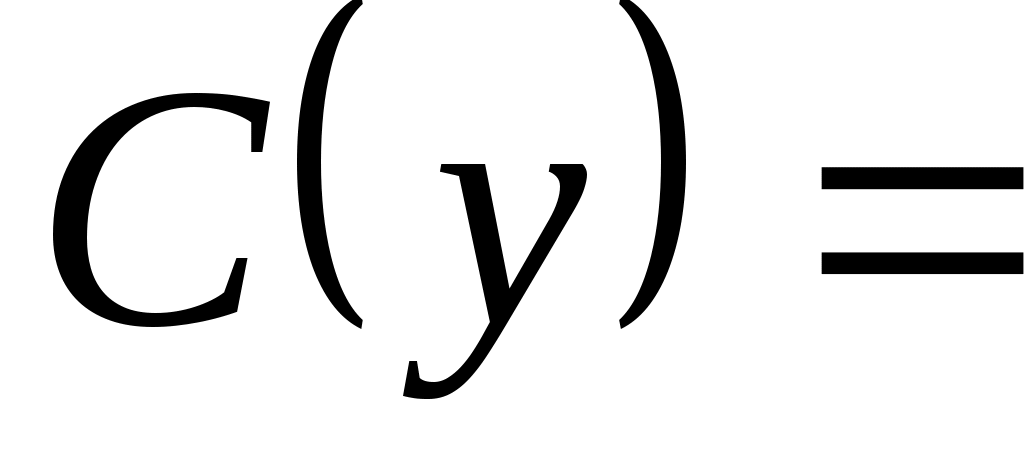 и и 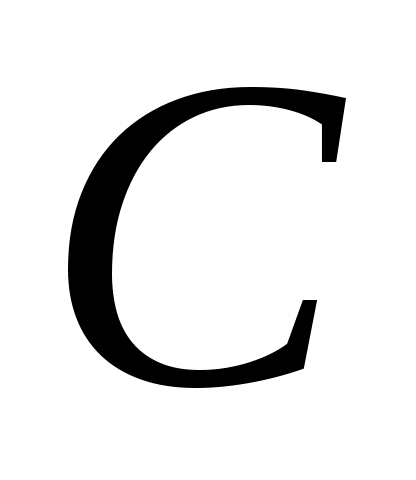 – нормальная функция выбора. Построить математическую задачу выбора. Является ли она разрешимой? – нормальная функция выбора. Построить математическую задачу выбора. Является ли она разрешимой?
2. Рассмотрим задачу выбора, в которой 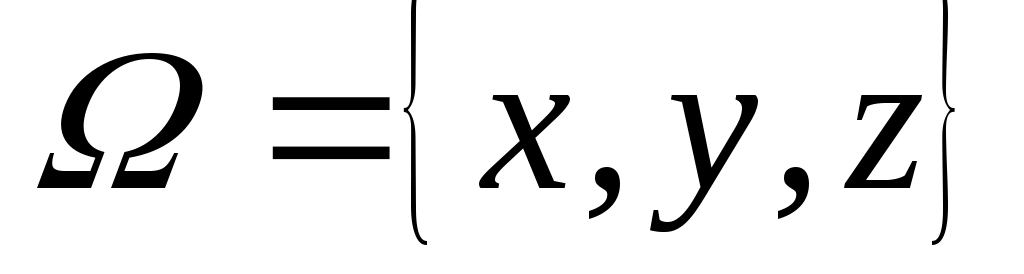 . Известно, что . Известно, что 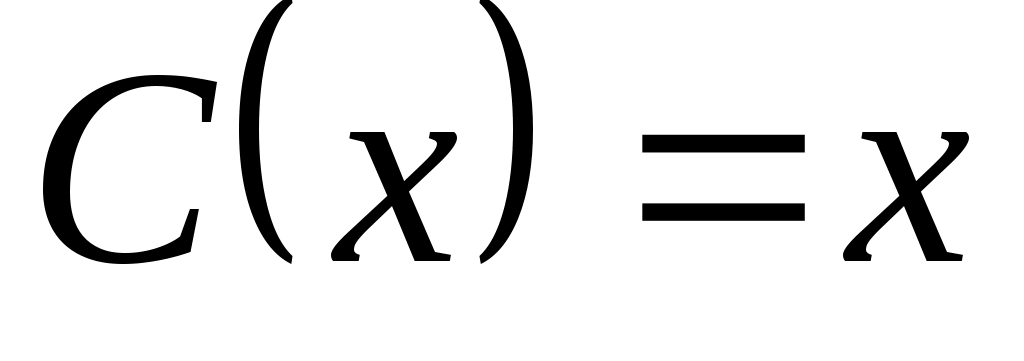 , , 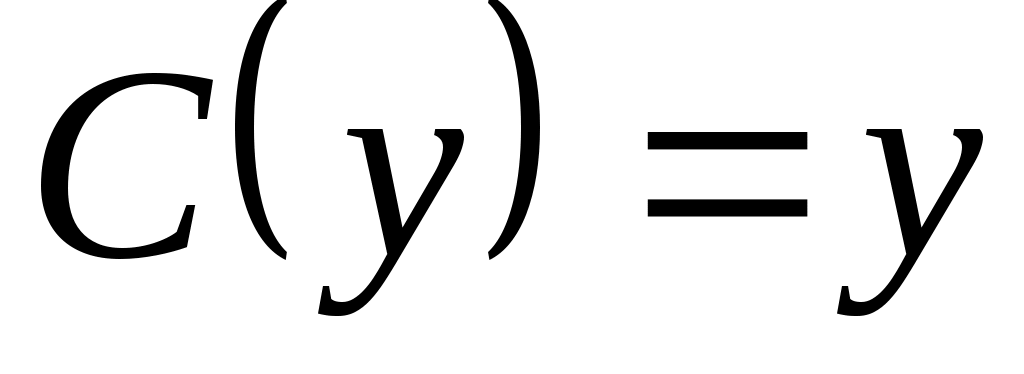 , , 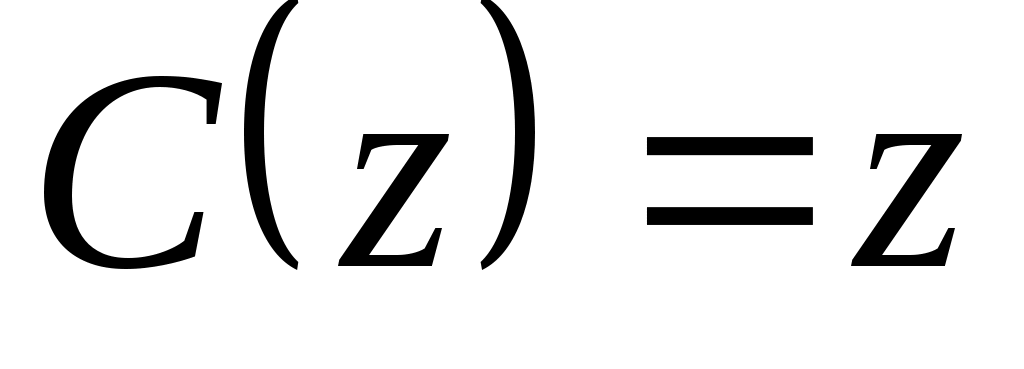 , , 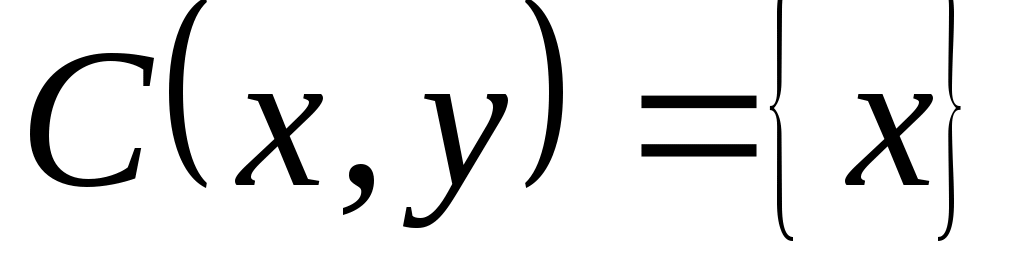 , , 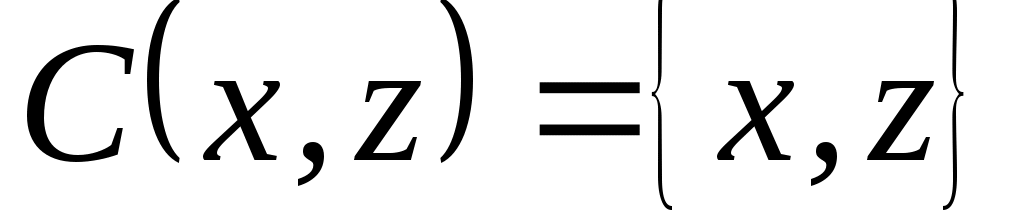 , , 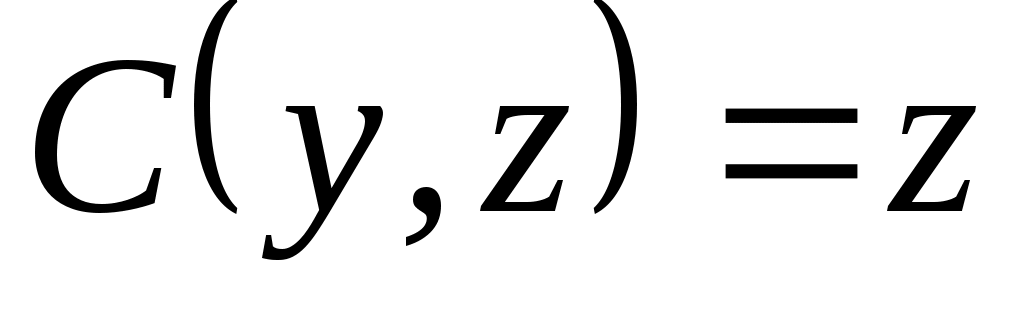 и и 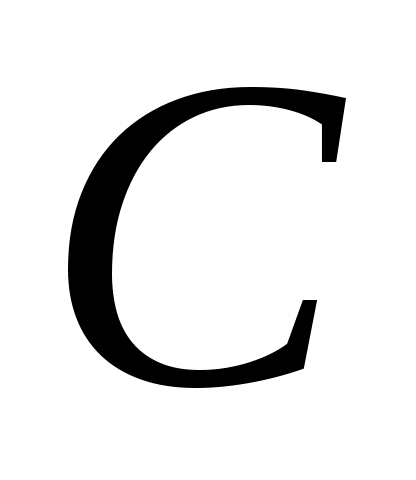 – нормальная функция выбора. Построить математическую задачу выбора. Является ли она разрешимой? – нормальная функция выбора. Построить математическую задачу выбора. Является ли она разрешимой?
II. Дополнительные упражнения
1. Пусть 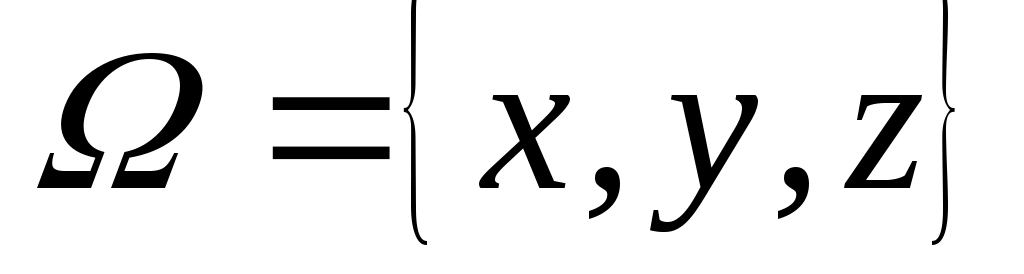 , , 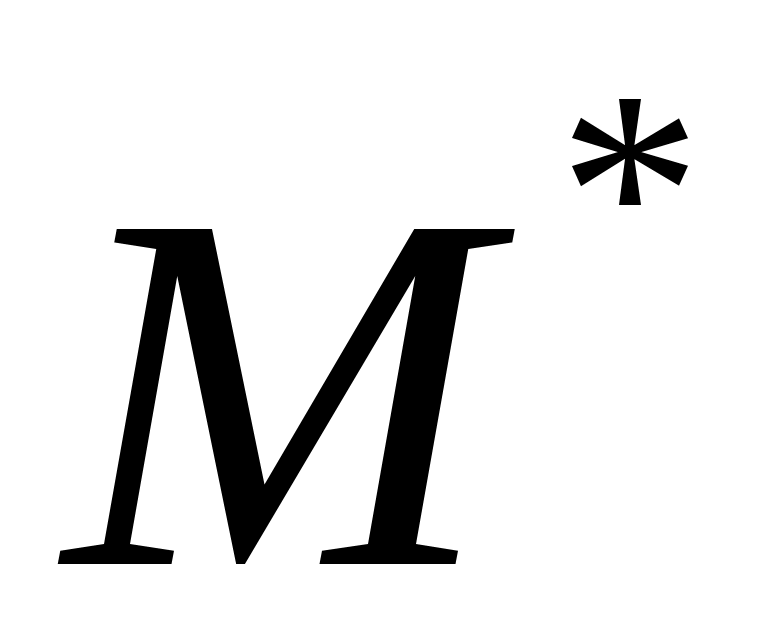 – множество функций выбора, являющихся объединением двух скалярных функций; – множество функций выбора, являющихся объединением двух скалярных функций; 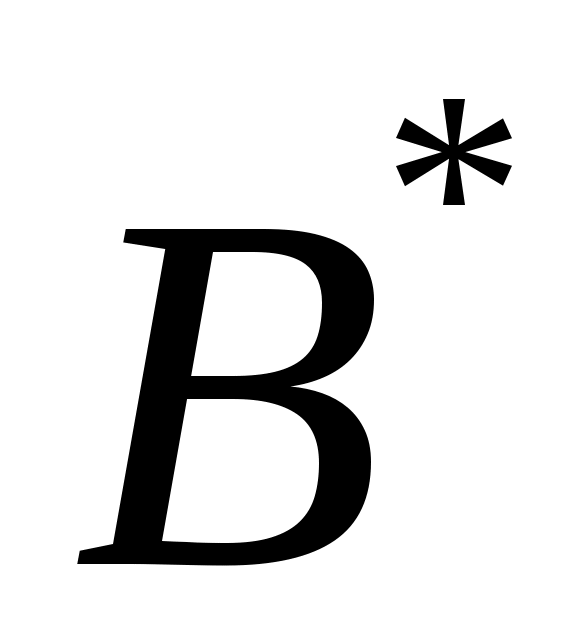 – все двухэлементные подмножества – все двухэлементные подмножества 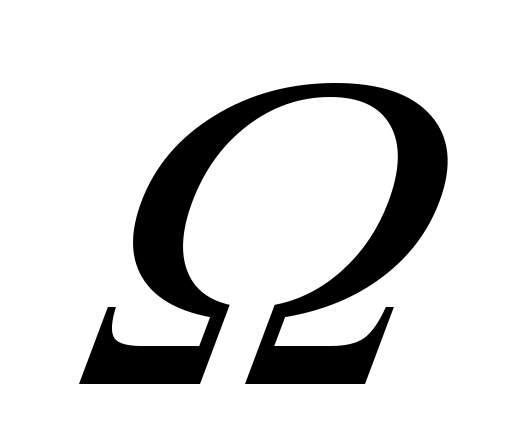 . Показать, что математическая задача . Показать, что математическая задача 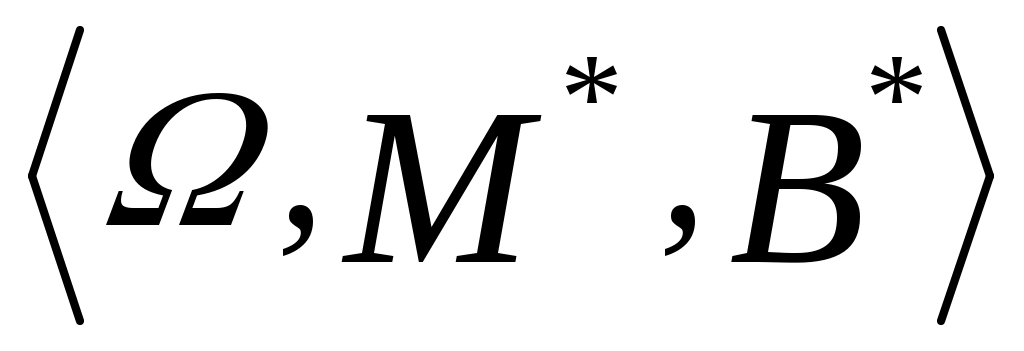 не является разрешимой. (Указание: рассмотреть следующие четыре скалярные функции выбора: не является разрешимой. (Указание: рассмотреть следующие четыре скалярные функции выбора:
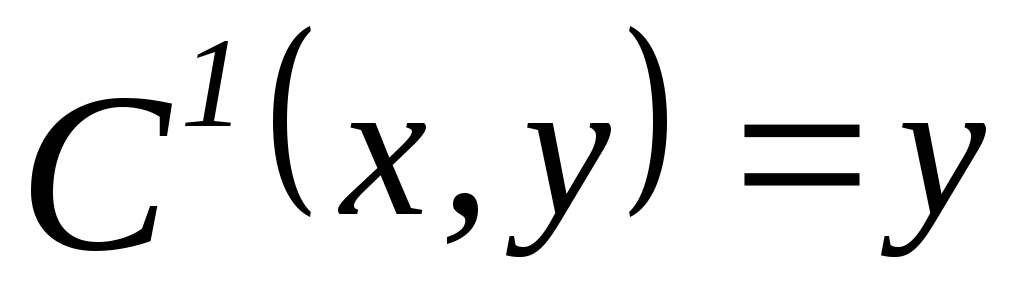 , , 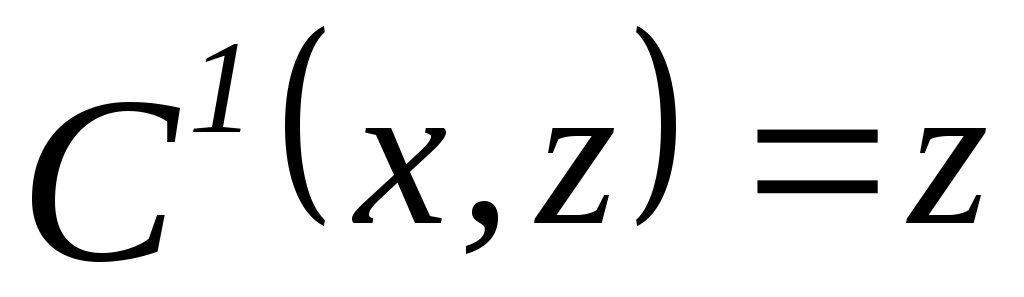 , , 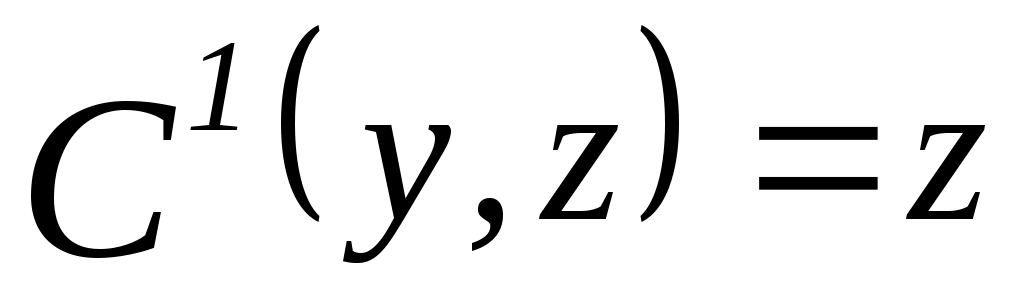 ; ;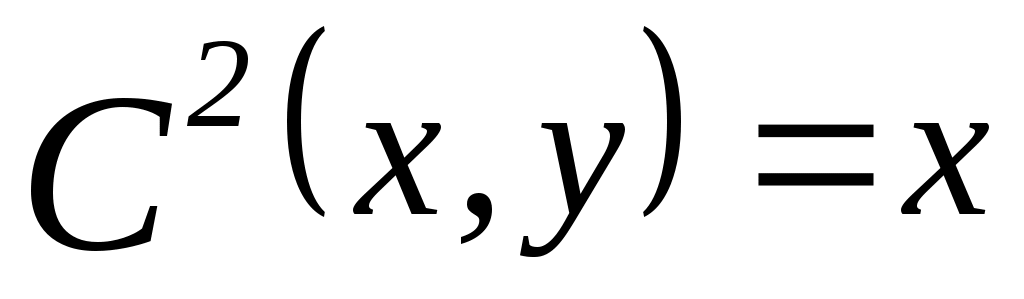 , , 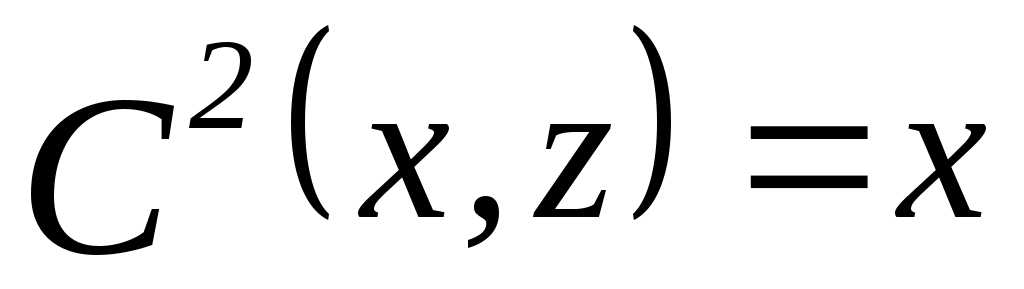 , , 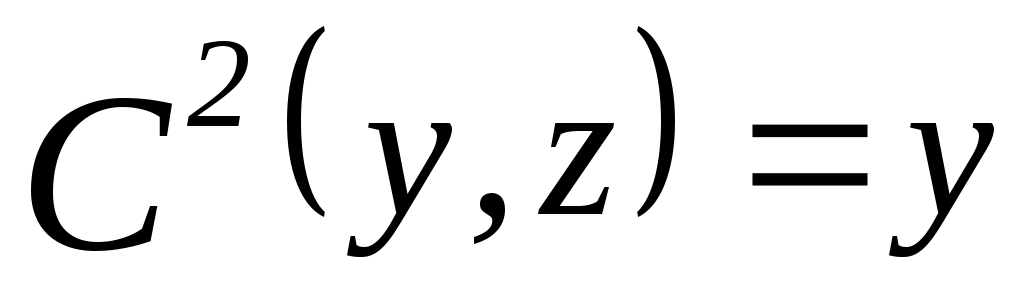 ; ; 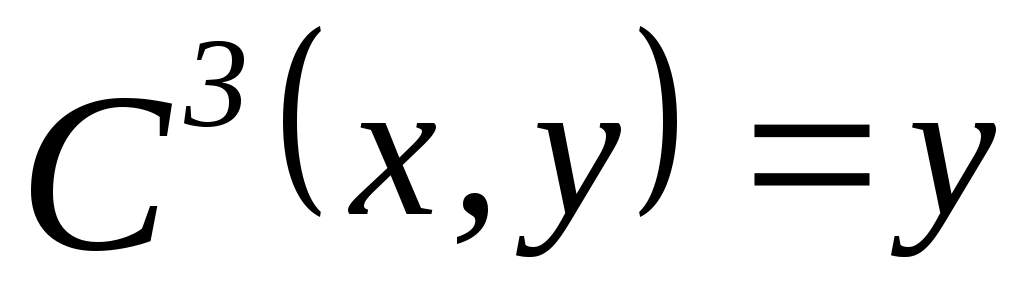 , , 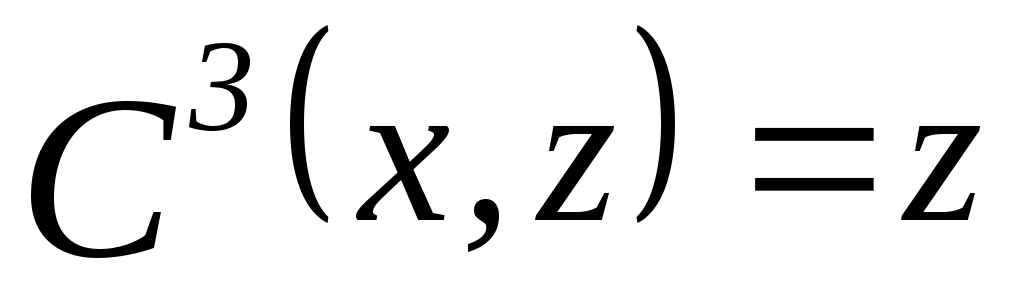 , , 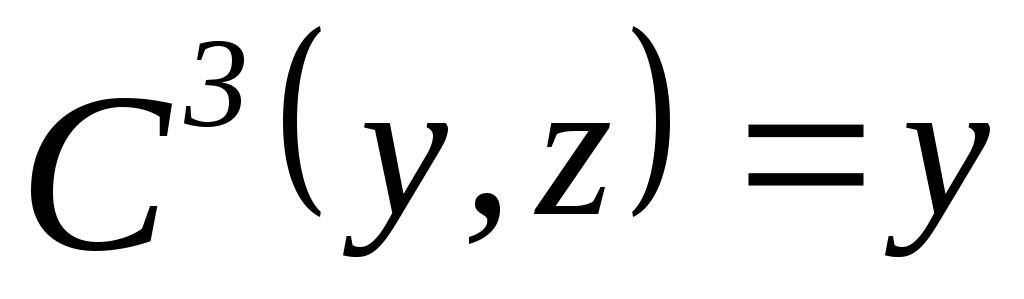 ; ;
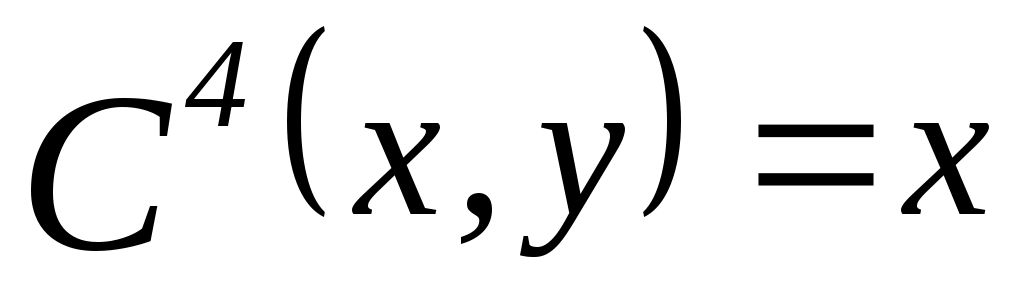 , , 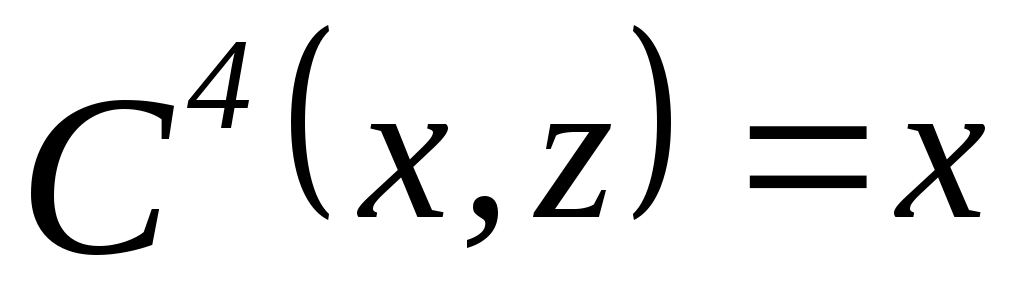 , , 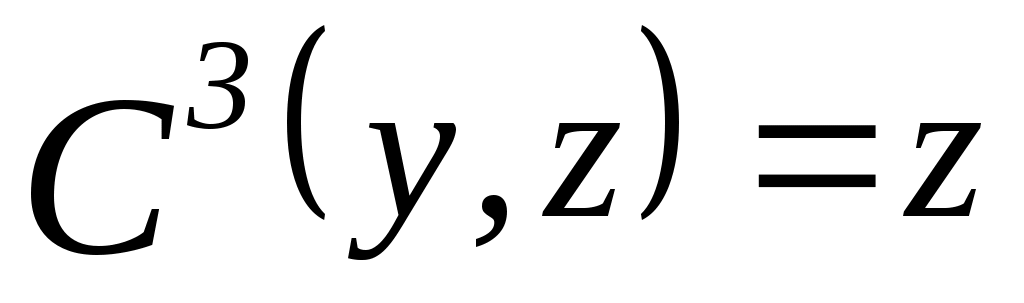 и и 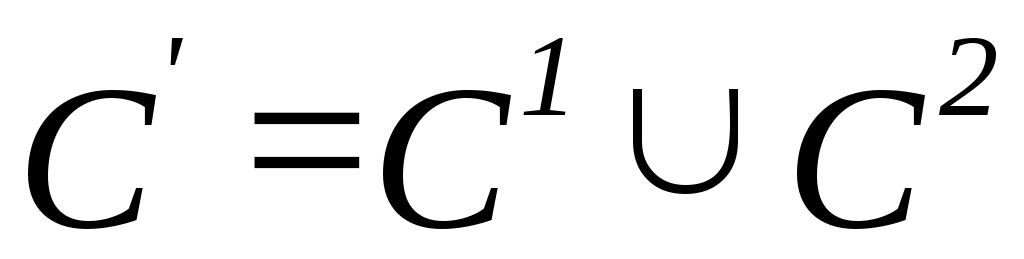 , , 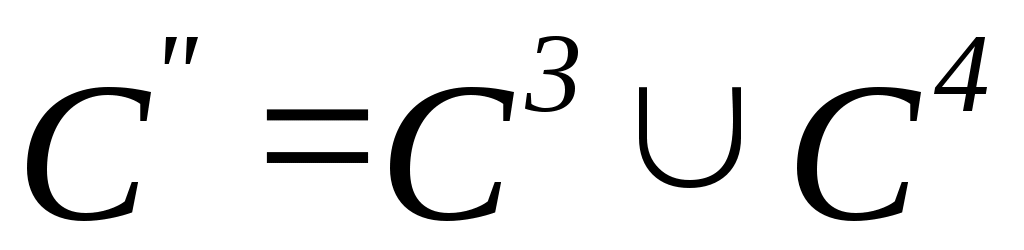 ) ) |
|
|
 Скачать 1.64 Mb.
Скачать 1.64 Mb.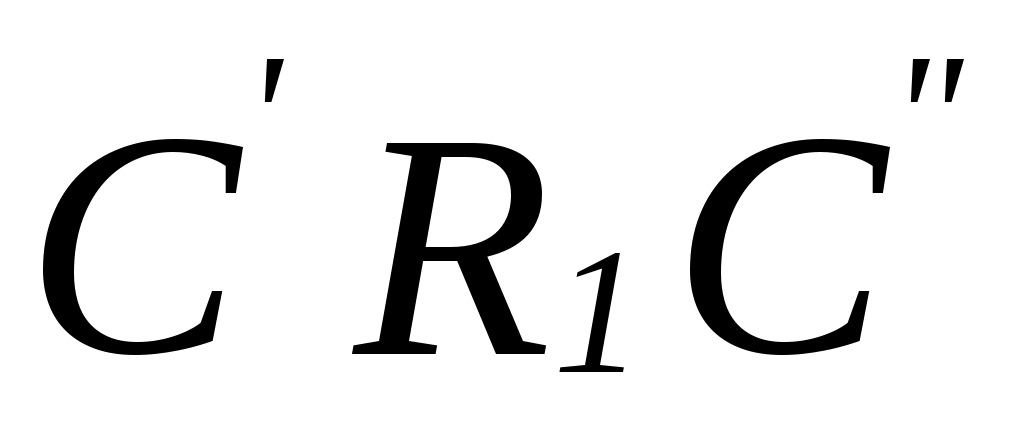
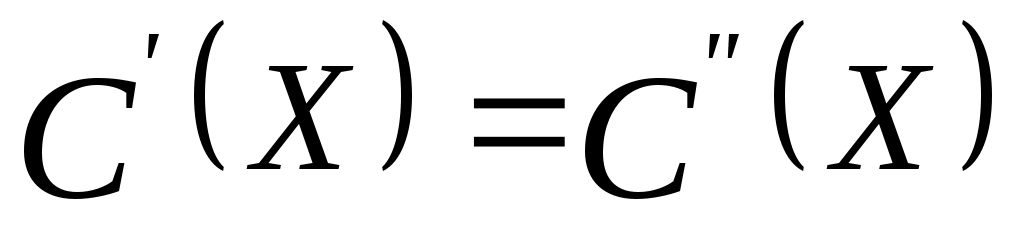 для всех
для всех 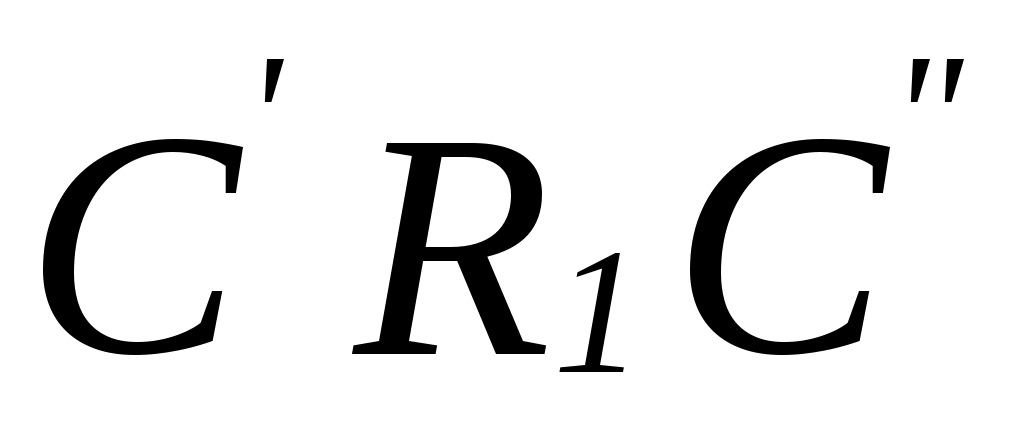
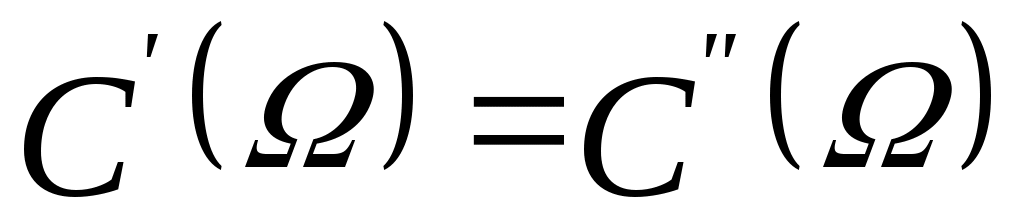 .
.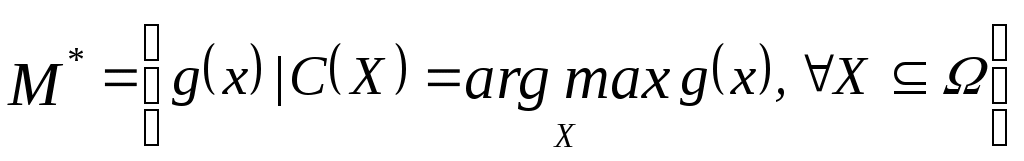 .
.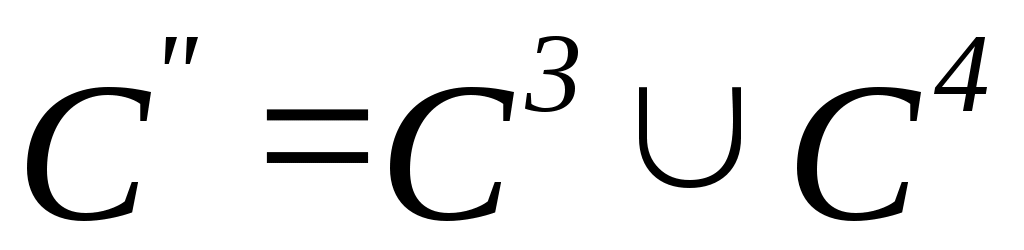 )
)