Электромагнетизм_задачи. Закон Кулона, где f сила взаимодействия двух точечных зарядов q 1 и q 2 в вакууме, r расстояние между зарядами

• Название: Закон Кулона, где f сила взаимодействия двух точечных зарядов q 1 и q 2 в вакууме, r расстояние между зарядами
• Анкор: Электромагнетизм_задачи.doc
• Дата: 30.10.2017
• Размер: 0.92 Mb.
• Имя файла: Электромагнетизм_задачи.doc
• Тип: Закон; #9963
• страница: 4 из 6

ЭЛЕКТРОМАГНЕТИЗМ
Основные формулы

Связь магнитной индукции B с напряженностью H магнитного поля:

,

где  - магнитная проницаемость изотропной среды; ₀ - магнитная постоянная. В вакууме =1, и тогда магнитная индукция в вакууме



Закон Био-Савара-Лапласа:

или ,

где dB - магнитная индукция поля, создаваемого элементом проводника длиной dl с током I; r - радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция;  - угол между радиус-вектором и направлением тока в элементе проводника.

Магнитная индукция в центре кругового тока:

,

где R - радиус кругового витка.

Магнитная индукция на оси кругового тока:

,

где h - расстояние от центра витка до точки, в которой определяется магнитная индукция.

Магнитная индукция поля прямого тока:

,

где r₀ - расстояние от оси проводника до точки, в которой определяется магнитная индукция.

Магнитная индукция поля, создаваемого отрезком провода с током ( см.рис.)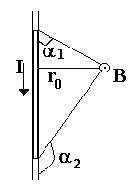





Обозначения ясны из рисунка. Направление вектора магнитной индукции B обозначено точкой - это значит, что B направлен перпендикулярно плоскости чертежа к нам.

При симметричном расположении концов провода относительно точки, в которой определяется магнитная индукция -cos₂=cos₁, тогда



Магнитная индукция поля соленоида:

,

где n - отношение числа витков соленоида к его длине.

Сила, действующая на проводник с током в магнитном поле (закон Ампера)

или ,

где l - длина проводника;  - угол между направлением тока в проводнике и вектором магнитной индукции B. Это выражение справедливо для однородного магнитного поля и прямого отрезка проводника. Если поле неоднородно и проводник не является прямым, то закон Ампера можно применять к каждому элементу проводника в отдельности:

.

Сила взаимодействия параллельных проводов с током:

,

где d - расстояние между проводами

Магнитный момент плоского контура с током:

,

где n -единичный вектор нормали к плоскости контура; I - сила тока, протекающего по контуру; S - площадь контура.

Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле:

или ,

где  - угол между векторами p_m и B

Отношение магнитного момента p_m к механическому L (моменту импульса) заряженной частицы, движущейся по круговой орбите:

,

где Q - заряд частицы; m- масса частицы.

Сила Лоренца

или ,

где v - скорость заряженность частицы;  - угол между векторами v и B.

Магнитный поток:

а) в случае однородного магнитного поля и плоской поверхности:

или ,

где S - площадь контура;  - угол между нормалью к плоскости контура и вектором магнитной индукции.

б) в случае неоднородного поля и произвольной поверхности:

(интегрирование по всей поверхности)

Потокосцепление (полный поток)



Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.

Работа по перемещению замкнутого контура в магнитном поле:



ЭДС индукции:

.

Разность потенциалов на концах проводника, движущегося со скоростью v в магнитном поле:

,

где l-длина проводника;  - угол между векторами v и B

Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур:

или ,

где R - сопротивление контура.

Индуктивность контура:

.

ЭДС самоиндукции:

.

Индуктивность соленоида:

,

где n - отношение числа витков соленоида к его длине; V - объем соленоида.

Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L:

а) (при замыкании цепи)

где  - эдс источника тока; t- время, прошедшее после замыкания цепи;

б) (при размыкании цепи),

где I₀- сила тока в цепи при t=0; t- время, прошедшее с момента замыкания цепи.

Энергия магнитного поля:



Объемная плотность энергии магнитного поля (отношение энергии магнитного поля соленоида к его объему):

или ,

где B - магнитная индукция; H- напряженность магнитного поля.

Примеры решения задач
Пример 1

Расстояние d между двумя длинными параллельными проводами равно 5см. По проводам в одном направлении текут одинаковые токи I=30А каждый. Найти напряженность H магнитного поля в точке, находящейся на расстоянии r₁=4см от одного и r₂=3см от другого провода.

Дано:

d=5см=0,05м

I=30А

r₁=4см=0,04м

r₂=3см=0,03м

H=?
Для нахождения напряженности H магнитного поля в точке А, определим направление векторов напряженности H₁ и H₂ полей, создаваемых каждым проводником в отдельности, и сложим их геометрически, то есть: H=H₁ + H₂ Так как направление векторов H₁ и H₂ совпадают с направлениями B₁ и B₂ векторов индукций соответствующих магнитных полей, и B₁=₀H₁, а B₂=₀H₂, то можно найти величину вектора B, а затем вычислить напряженность H.

Модуль индукции найдем по теореме косинусов: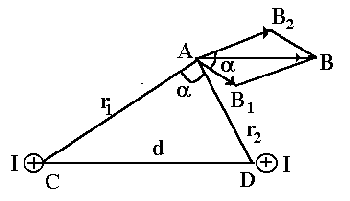

(1)


Значение индукций B₁ и B₂ выражаются соответственно через силу тока I и расстояния r₁ и r₂от провода до точки, индукцию в которой мы вычисляем:

, .

Подставляя B₁ и B₂ в формулу (1) и вынося общий множитель за знак корня, получим:

(2)

Вычисляем величину cos. Заметим, что =ДАС. Поэтому, по теореме косинусов запишем:

,

d - расстояние между проводами.

Отсюда:



Вычисляем:

Подставив в формулу (2) значения ₀, I, r₁, r₂, найдем:

(Тл),

(А/м)

Пример2

Вычислить радиус R дуги окружности, которую описывает протон в магнитном поле с индукцией B=15мТл, если скорость v протона равна 2Мм/с.

Дано:

B=15мТл=1510^-3Тл

v=2Мм/с=210⁶м/с

R=?
На движущийся в магнитном поле протон действует сила Лоренца F_л (действием силы тяжести можно пренебречь). Вектор силы Лоренца перпендикулярен вектору скорости и, следовательно, по второму закону Ньютона, сообщает протону нормальное ускорение a_n:

,

получаем: (1)

q, v, m - заряд, скорость, масса протона.

B - индукция магнитного поля, R - радиус кривизны траектории,  - угол между направлениями векторов скорости и индукции ( в нашем случае и =90⁰, sin=1).

Из формулы (1) найдем:



Масса и заряд протона соответственно равны:

q=+e=1,610^-19Кл.

M_p=1,6710^-27кг.

(м)

Пример3

Соленоид индуктивностью L=4мГн содержит N=600 витков. Определить магнитный поток Ф, если сила тока I, протекающего по обмотке, равна 12А

Дано:

L=4мГн=410^-3Гн

N=600

I=12А

Ф=?

Магнитный поток определяется как:

Индуктивность соленоида определяется по формуле: ,

где n - число витков, приходящиеся на один метр длины соленоида, V - объем соленоида,  - магнитная проницаемость среды, ₀=410^-7Гн/м.

Так как , l - длина соленоида, , получаем:



Или

Магнитную индукцию соленоида можно определить как:



Окончательно выводим формулу для магнитного потока:



(Вб)
1. Сила Ампера.

1. 
   Прямой провод, по которому течет ток 1 кА, расположен в однородном магнитном поле перпендикулярно линиям индукции. С какой силой F действует поле на отрезок провода длиной 1 м, если магнитная индукция В равна 1 Тл?
   
2. 
   Прямой провод длиной 10 см, по которому течет ток 20 А, находится в однородном магнитном поле с индукцией В=0,01 Тл. Найти угол между направлениями вектора В и тока, если на провод действует сила 10 мН.
   
3. 
   Квадратная проволочная рамка расположена в одной плоскости с длинным прямым проводом так, что две ее стороны параллельны проводу. По рамке и проводу текут одинаковые токи I=1 кА. Определить силу F, действующую на рамку, если ближайшая к проводу сторона рамки находится на расстоянии, равном ее длине.
   
4. 
   Тонкий провод в виде дуги, составляющей треть кольца радиусом 15 см, находится в однородном магнитном поле (В=20 мТл.). По проводу течет ток I=20 А. Плоскость, в которой лежит дуга, перпендикулярна линиям магнитной индукции, и проводящие провода находятся вне поля. Определить силу F, действующую на провод.
   
5. 
   По тонкому проводу в виде кольца радиусом 20 см течет ток I=100 А. Перпендикулярно плоскости кольца возбуждено однородное магнитное поле с индукцией 20 мТл. Найти силу F, растягивающую кольцо.
   
6. 
   Двухпроводная линия состоит из длинных параллельных прямых проводов, находящихся на расстоянии 4 мм друг от друга. По проводам текут одинаковые токи I=50 А. Определить силу взаимодействия токов, приходящуюся на единицу длины провода.
   
7. 
   Шины генератора представляют собой две параллельные медные полосы длиной 2 м каждая, отстоящие друг от друга на 20 см. Определить силу взаимного отталкивания шин в случае короткого замыкания, когда по ним течет ток I=10 кА.
   
8. 
   По двум проводникам длиной 1 м каждый текут одинаковые токи. Расстояние между проводами равно 1 см. Токи взаимодействуют с силой F=1 мН. Найти силу тока I в проводах.
   
9. 
   По трем параллельным прямым проводам, находящимся на расстоянии а=10 см друг от друга, текут одинаковые токи I=100 А. В двух проводах направления токов совпадают. Вычислить силу F, действующую на отрезок длиной L= 1 м каждого провода.
   
10. 
    По двум тонким проводам, изогнутым в виде кольца радиусом 10 см, текут одинаковые токи I = 10 А в каждом. Найти силу взаимодействия этих колец, если плоскости, в которых лежат кольца, параллельны, а расстояние между центрами колец равно 1 мм.
    
11. 
    По двум одинаковым плоским контурам со стороной а=20 см текут токи I=10 А в каждом. Определить силу взаимодействия контуров, если расстояние d между соответственными сторонами контуров равно 2 мм.
    
12. 
    По тонкому проволочному полукольцу радиусом R=50 см течет ток I=50 А. Перпендикулярно плоскости полукольца возбуждено однородное магнитное поле с индукцией В=0,01 Тл. Найти силу, растягивающую полукольцо.
    
13. 
    Прямоугольная рамка со сторонами а=40 см и b=30 см расположена в одной плоскости с бесконечным прямолинейным проводом с током I=6 А так, что длинные стороны рамки параллельны проводу. Сила тока в рамке I₁=1 А. Определить силы, действующие на каждую из сторон рамки, если ближайшая к проводу сторона рамки находится на расстоянии с=10 см, а ток в ней сонаправлен току I.
    
14. 
    Шины электростанции представляют собой параллельные медные полосы длиной 3 м, находящиеся на расстоянии 50 см. При коротком замыкании по ним может пройти ток 10000 А. С какой силой взаимодействуют при этом шины?
    
15. 
    Две небольшие одинаковые катушки расположены так, что их оси лежат на одной прямой. Расстояние между катушками 200 мм значительно превышает их линейные размеры. Число витков каждой катушки N=100, радиус витков r=10 мм. С какой силой взаимодействуют катушки, когда по ним течет одинаковый ток I=0,10 А?
    
16. 
    Рядом с длинным прямым проводом, по которому течет ток I₁=30 А, расположена квадратная рамка с током I₂=2А. Рамка и провод лежат в одной плоскости. Проходящая через середины противолежащих сторон ось рамки параллельна проводу и отстоит от него на расстояние b=30 мм. Сторона рамки а=20 мм. Найти силу, действующую на рамку , и работу, которую надо совершить, чтобы повернуть рамку вокруг ее оси на 180.
    
17. 
    По двум тонким проводам, изогнутым в виде кольца радиусом 20 см, текут одинаковые токи I = 0,1 А в каждом. Найти силу взаимодействия этих колец, если плоскости, в которых лежат кольца, параллельны, а расстояние между центрами колец равно 1 мм.
    
18. 
    По двум одинаковым плоским контурам со стороной а=10 см текут токи I=0,1 А в каждом. Определить силу взаимодействия контуров, если расстояние d между соответственными сторонами контуров равно 3 см.
    
19. 
    Прямой провод длиной 50 см, по которому течет ток 10 А, находится в однородном магнитном поле с индукцией В=0,01 Тл. Найти угол между направлениями вектора