|
|
Электромагнетизм_задачи. Закон Кулона, где f сила взаимодействия двух точечных зарядов q 1 и q 2 в вакууме, r расстояние между зарядами
ЭЛЕКТРИЧЕСТВО
Основные формулы
Закон Кулона
 , ,
где F - сила взаимодействия двух точечных зарядов Q1 и Q2 в вакууме, r - расстояние между зарядами
Напряженность и потенциал электростатического поля
Е=F/Q; =П/Q; =A/Q,
где F - сила, действующая на точечный заряд Q, помещенный в данную точку поля; П - потенциальная энергия заряда Q; A - работа перемещения заряда Q из данной точки поля за его пределы.
Напряженность и потенциал электростатического поля точечного заряда Q на расстоянии r от него
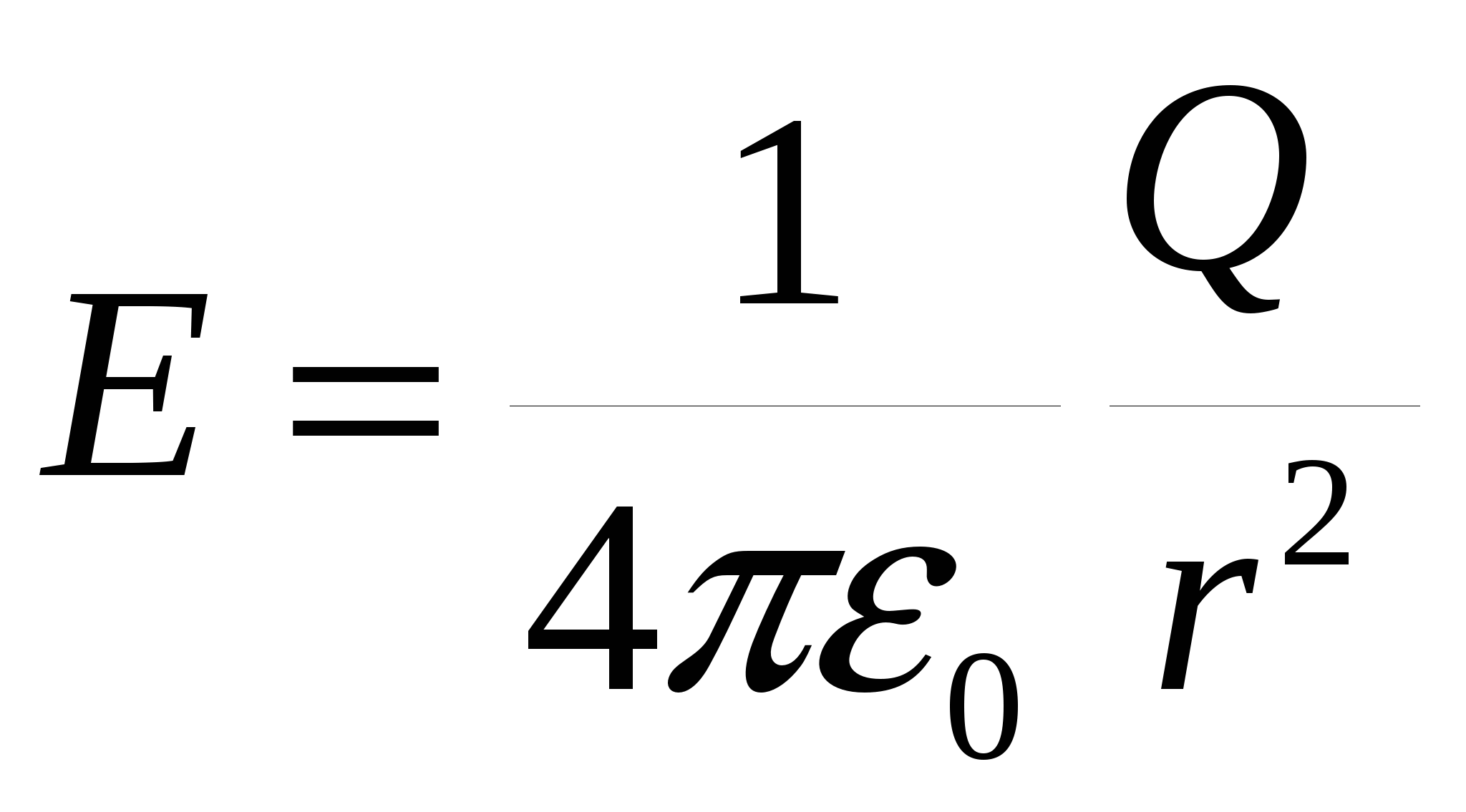 , ,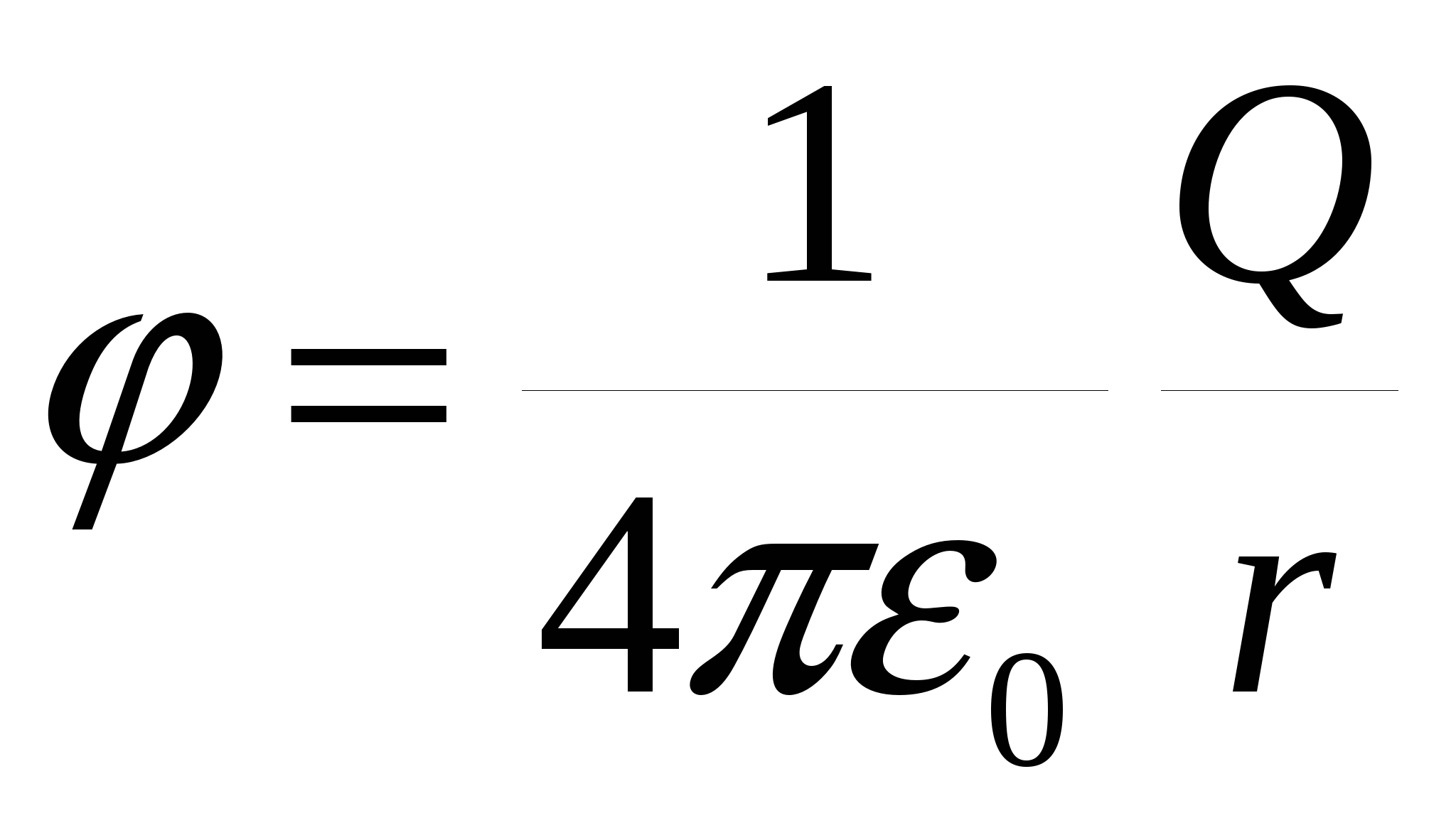 . .
Принцип суперпозиции электростатических полей
Е=Еi,
где Еi - напряженность, создаваемая зарядом Qi.
Связь между напряженностью и потенциалом электростатического поля
Е=-grad .
Линейная, поверхностная и объемная плотности зарядов
=dQ/dl =dQ/ds =dQ/dV
Теорема Гаусса для электростатического поля в вакууме
Напряженность поля, создаваемого равномерно заряженной бесконечной плоскостью
Е=/(20)
Напряженность поля, создаваемого равномерно заряженной сферической поверхностью радиусом R c общим зарядом Q на расстоянии r от центра сферы
Е=0 при r
 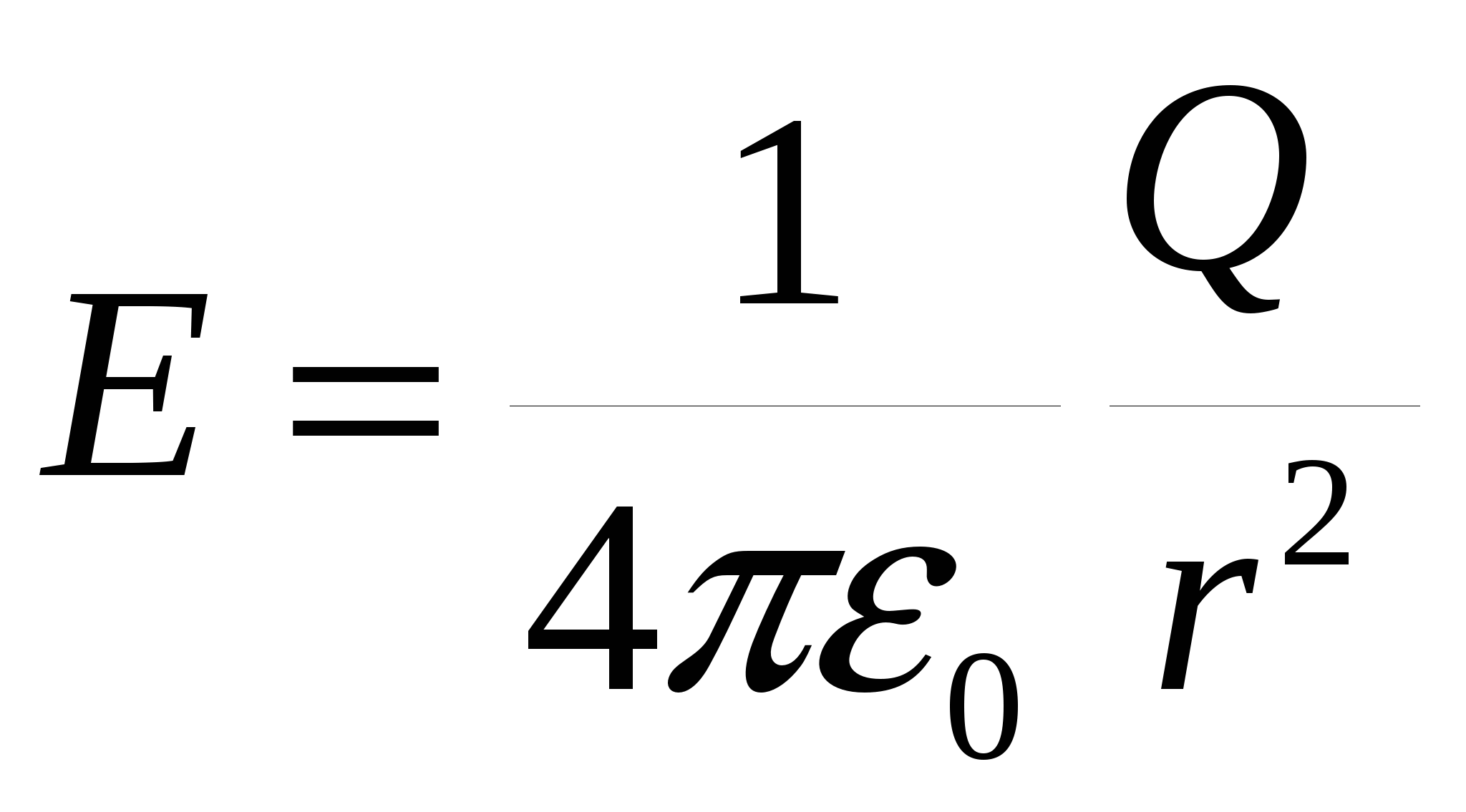 при r>R. при r>R.
Напряженность поля, создаваемого объемно заряженным шаром радиусом R c общим зарядом Q на расстоянии r от центра шара
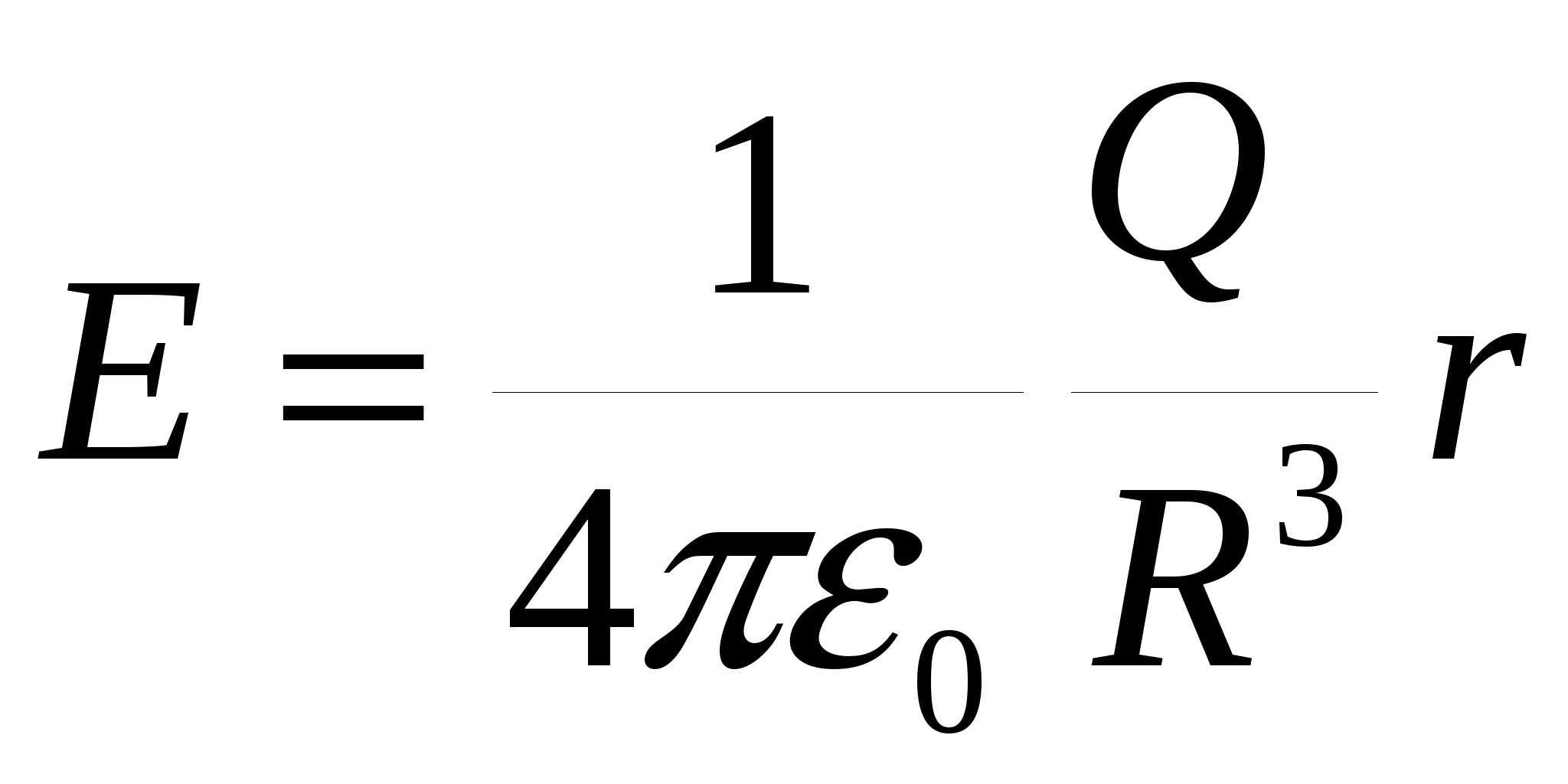 при r при r
 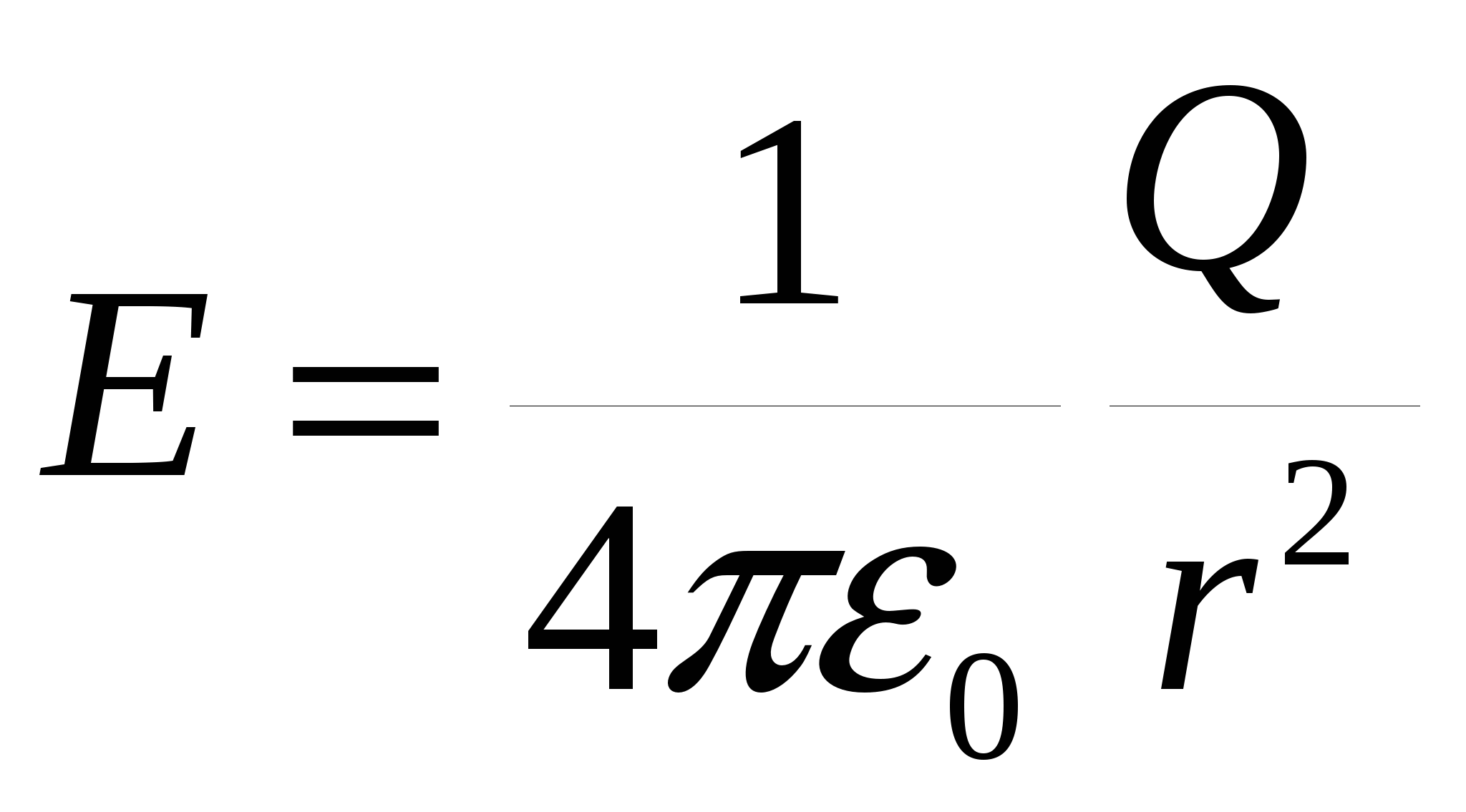 при r>R. при r>R.
Напряженность поля, создаваемого равномерно заряженным цилиндром радиусом R на расстоянии r от оси цилиндра
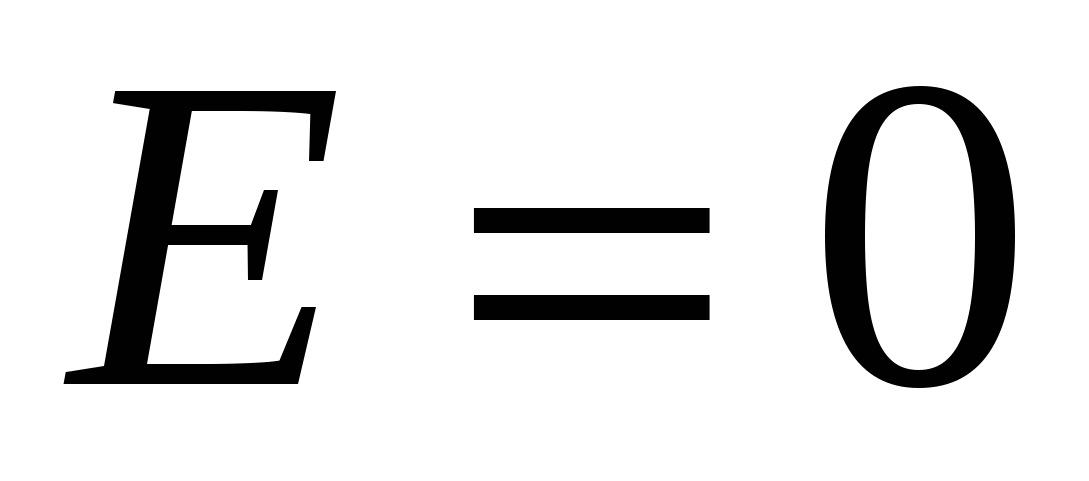 при r при r
 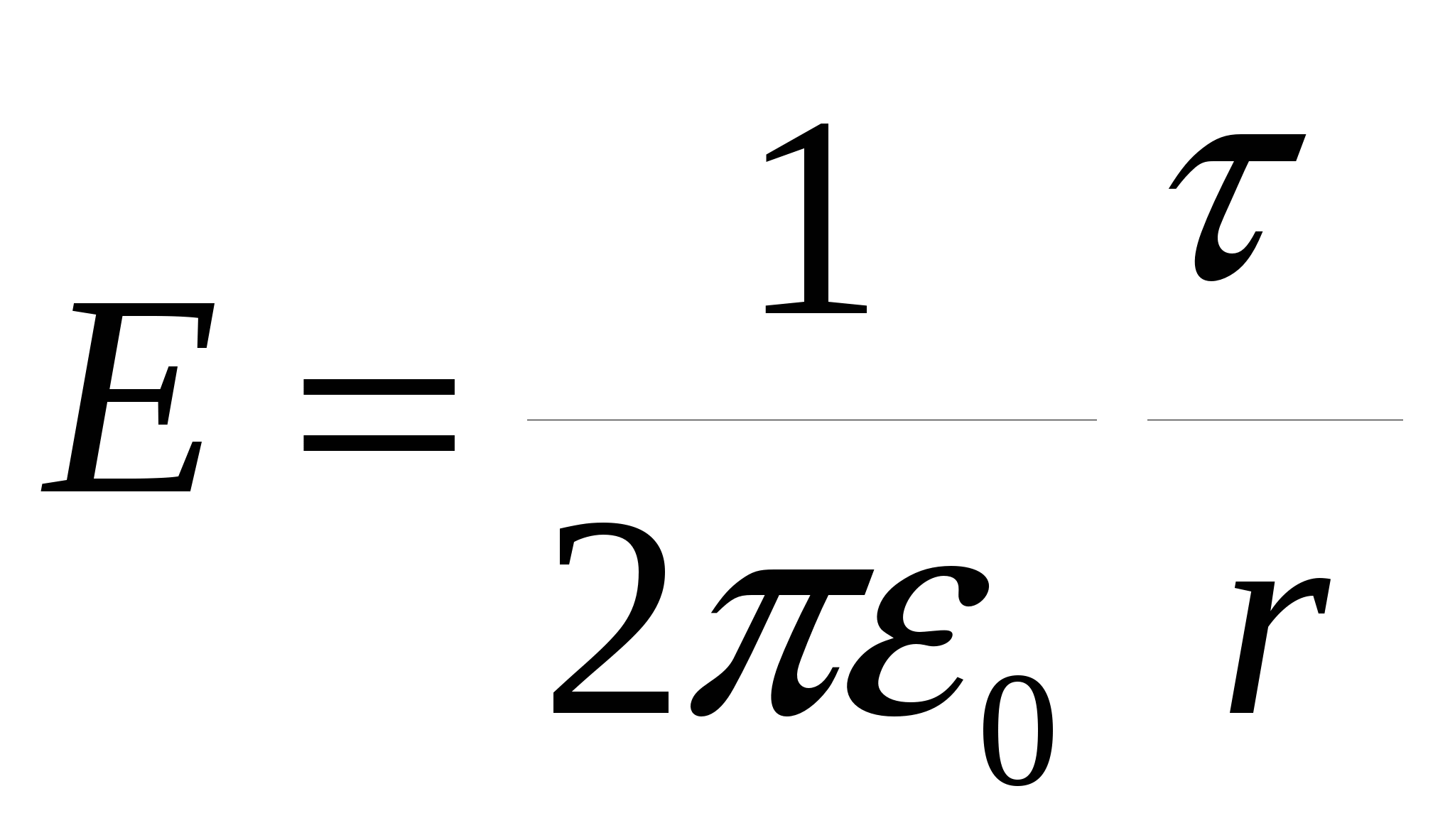 при r>R. при r>R.
Циркуляция вектора напряженности электростатического поля вдоль замкнутого контура
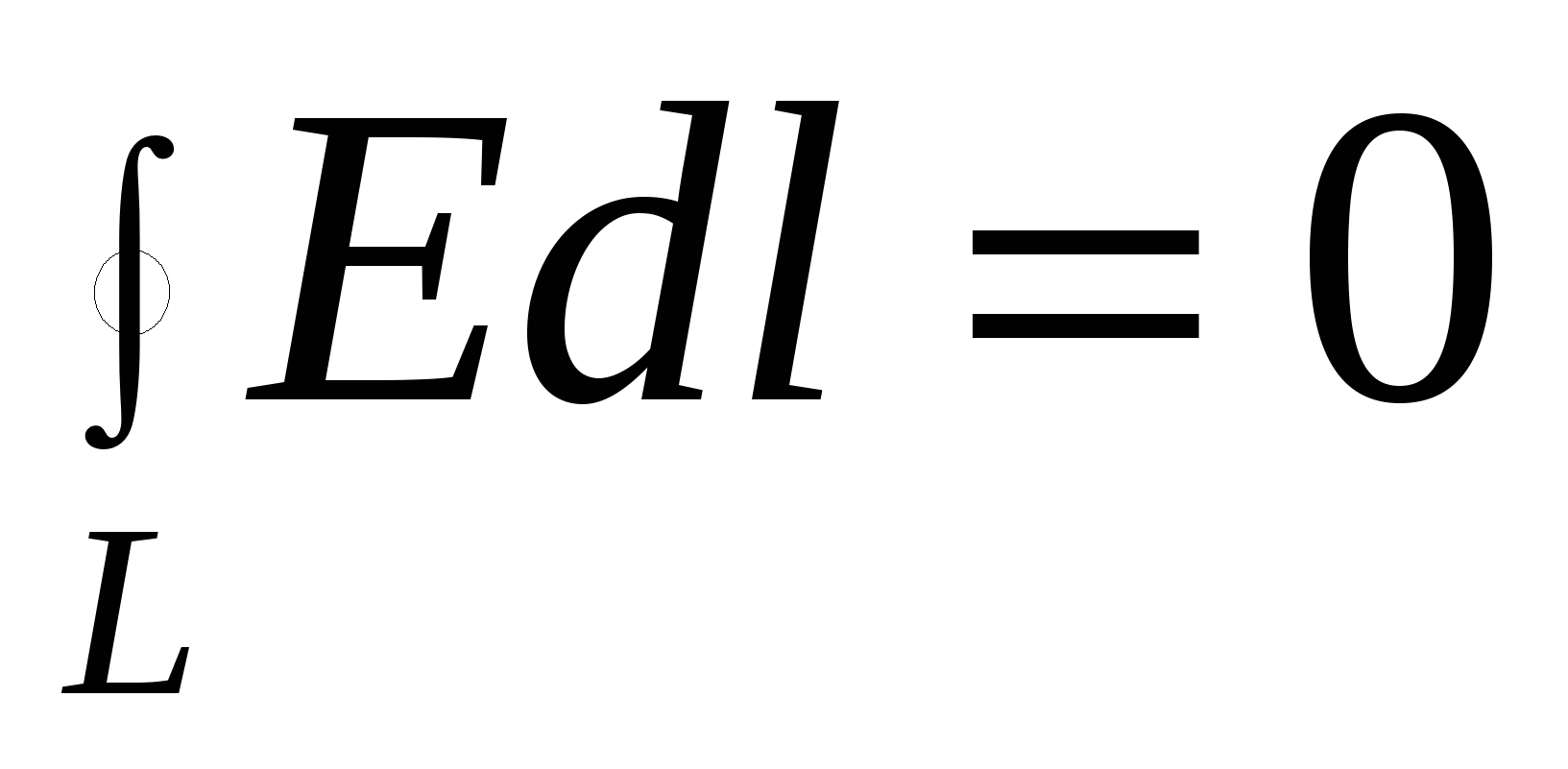
Работа, совершаемая силами электростатического поля при перемещении заряда Q из точки 1 в точку 2
А12=Q(1-2)
Связь между векторами электрического смещения и напряженностью электростатического поля
D=0 E
Теорема Гаусса для электростатического поля в диэлектрике
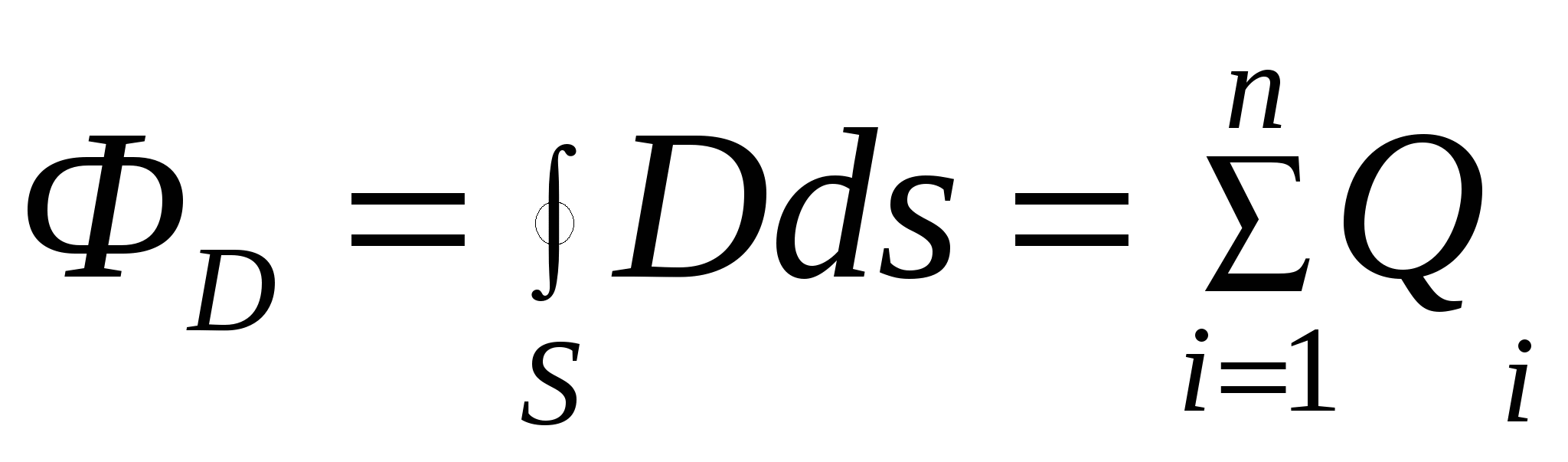 , ,
где 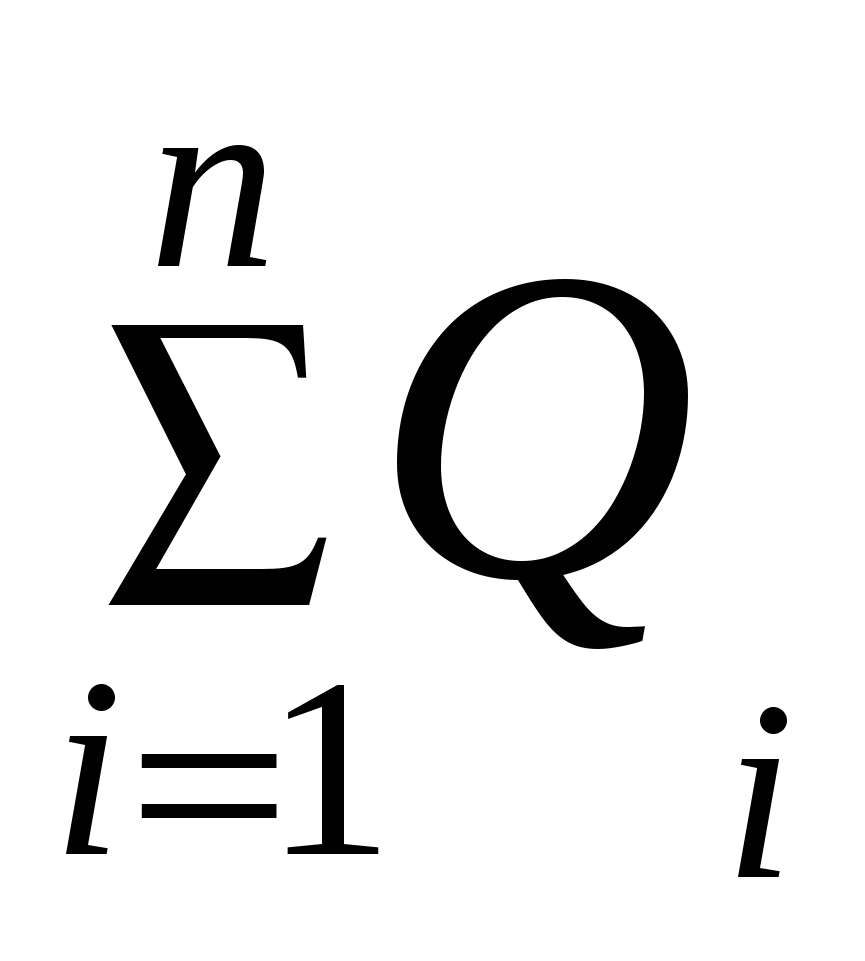 - алгебраическая сумма зарядов, заключенных внутри поверхности S. - алгебраическая сумма зарядов, заключенных внутри поверхности S.
Электроемкость уединенного проводника
C=Q/,
Где Q - заряд, сообщенный проводнику, - потенциал проводника.
Емкость плоского конденсатора
С=0 S/d,
где S - площадь пластин конденсатора, d - расстояние между пластинами.
Емкость сферического конденсатора
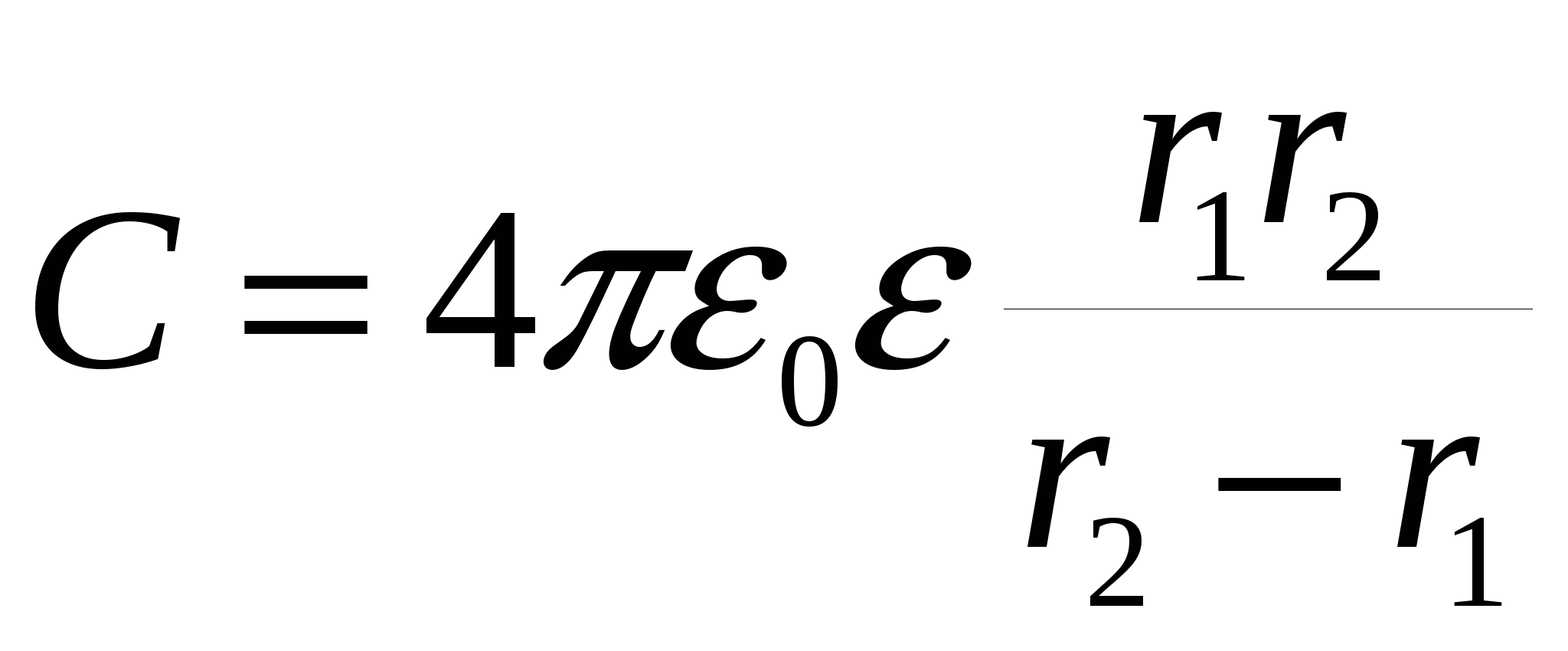 , ,
где r1 и r2 - радиусы концентрических сфер.
Емкость системы конденсаторов при последовательном и параллельном соединении
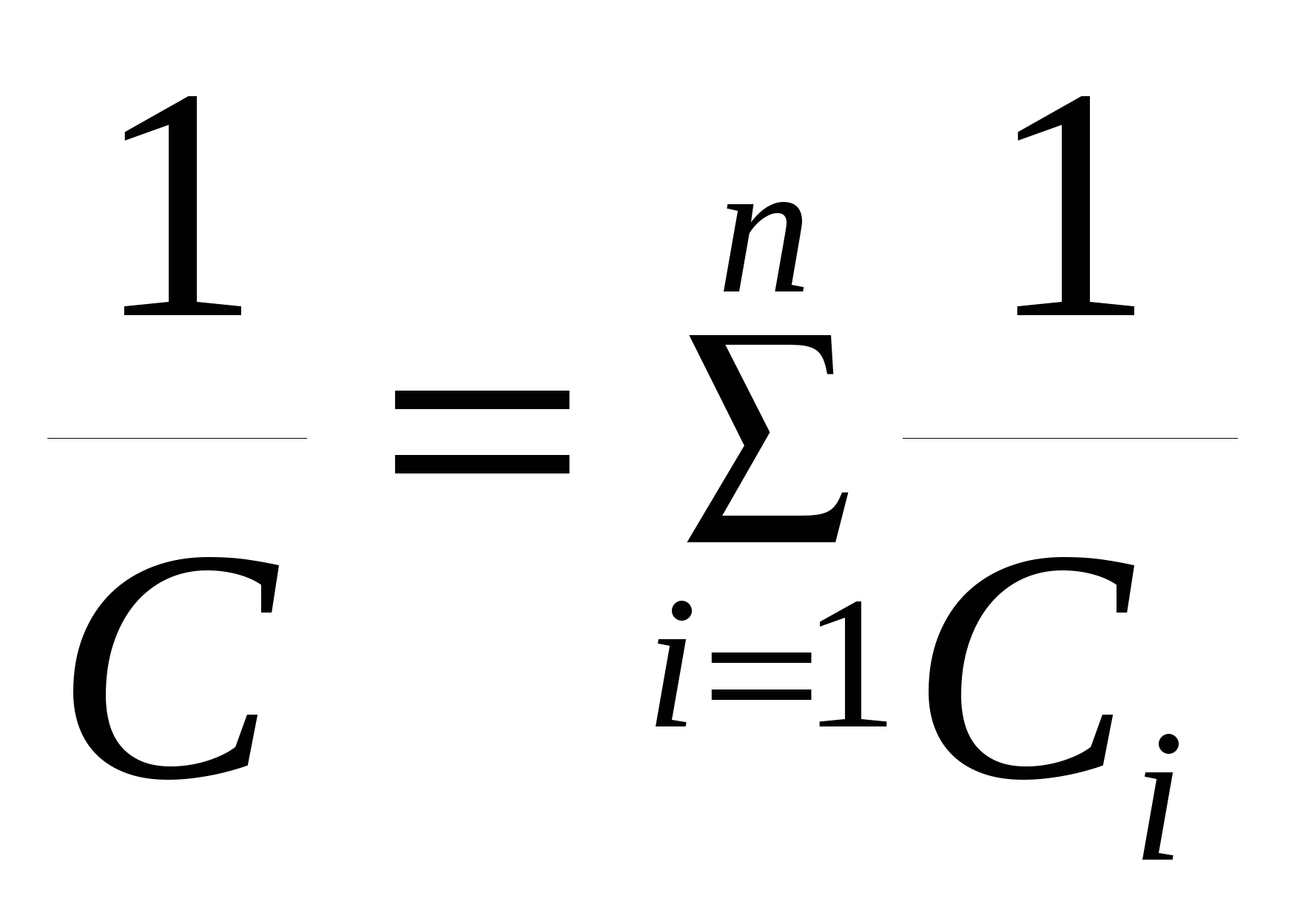 и и 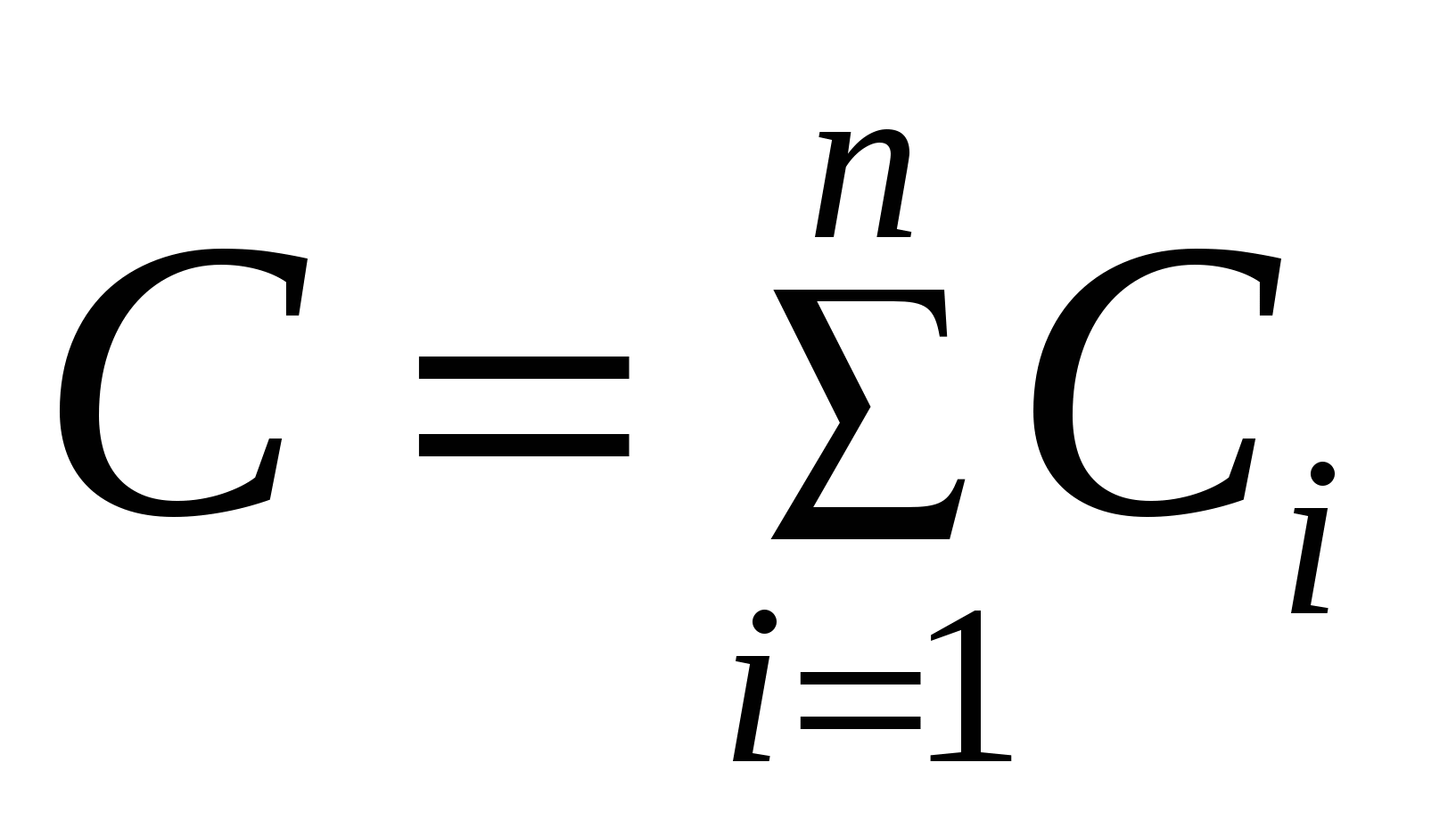 , ,
где Сi - емкость i-го конденсатора, n - число конденсаторов в батарее.
Энергия заряженного конденсатора
W=QU/2, W=CU2/2, W=Q2/2C.
Сила и плотность электрического тока
I=dQ/dt, j=I/S,
где Q - заряд, прошедший через поперечное сечение S проводника за время t.
Плотность тока в проводнике
j=ne,
где n - концентрация зарядов, - скорость их движения в проводнике.
R=l/S, G=1/R,
где - удельное сопротивление проводника, S - площадь поперечного сечения, l - его длина.
Закон Ома:
для однородного участка цепи
I=U/R,
для неоднородного участка цепи
I=(1- 2+E12)/R,
для замкнутой цепи
I=E/R,
где U - напряжение на участке цепи, R - сопротивление цепи (участка цепи), 1- 2 - разность потенциалов на концах участка, Е12 - ЭДС источников тока, входящих в участок, Е - ЭДС всех источников тока цепи.
Работа тока
A=IUt=I2Rt=U2t/R
Мощность тока
P=UI= I2R=U2/R
Закон Джоуля-Ленца
Q= IU=I2R=U2/R
Правила Кирхгофа
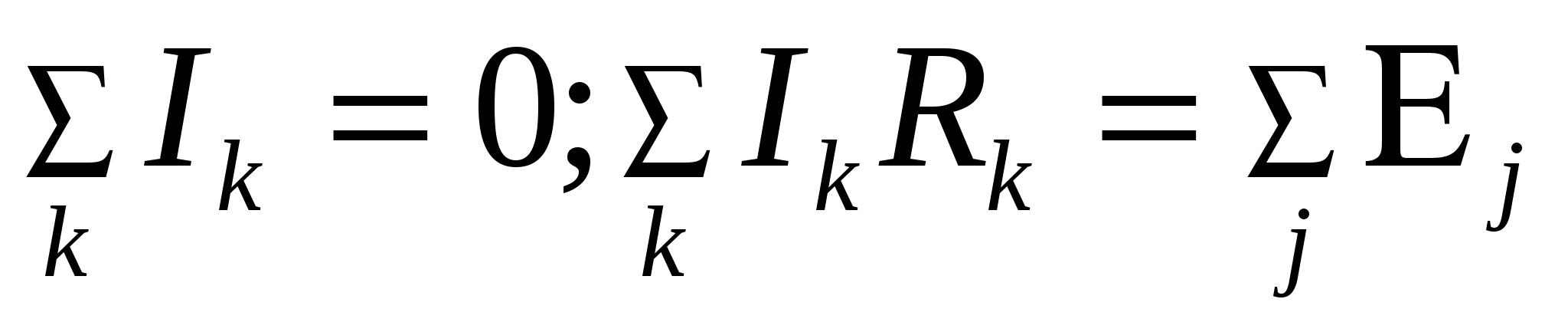
Примеры решения задач
В вершинах квадрата находятся одинаковые заряды Q=1 нКл. Какой отрицательный заряд q надо поместить в центре квадрата, чтобы сила притяжения с его стороны уравновесила силы отталкивания положительных зарядов?
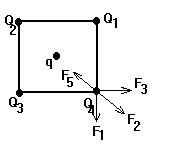
Так как все заряды находятся в равновесии, достаточно рассмотреть силы, действующие на один из зарядов: F1+F2+F3+F5=0, где F1, F2, F3 и F5 - силы, действующие на заряд Q4 со стороны зарядов Q1, Q2, Q3 и q.
Видим, что силы F1 и F3 равны, то равнодействующая этих сил в скалярной форме R=2F1cos.
Запишем сумму всех сил в скалярной форме:F5=R+F2. (1)
Найдем проекции сил F1, F2, и F5:
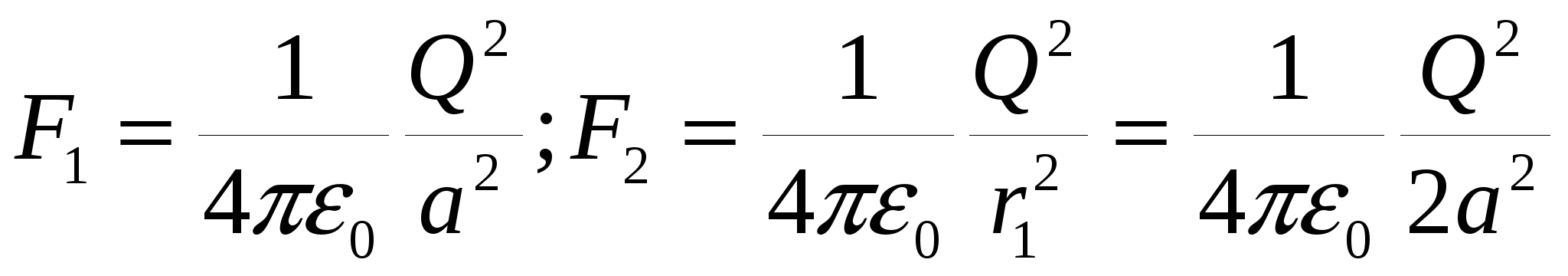 ; ;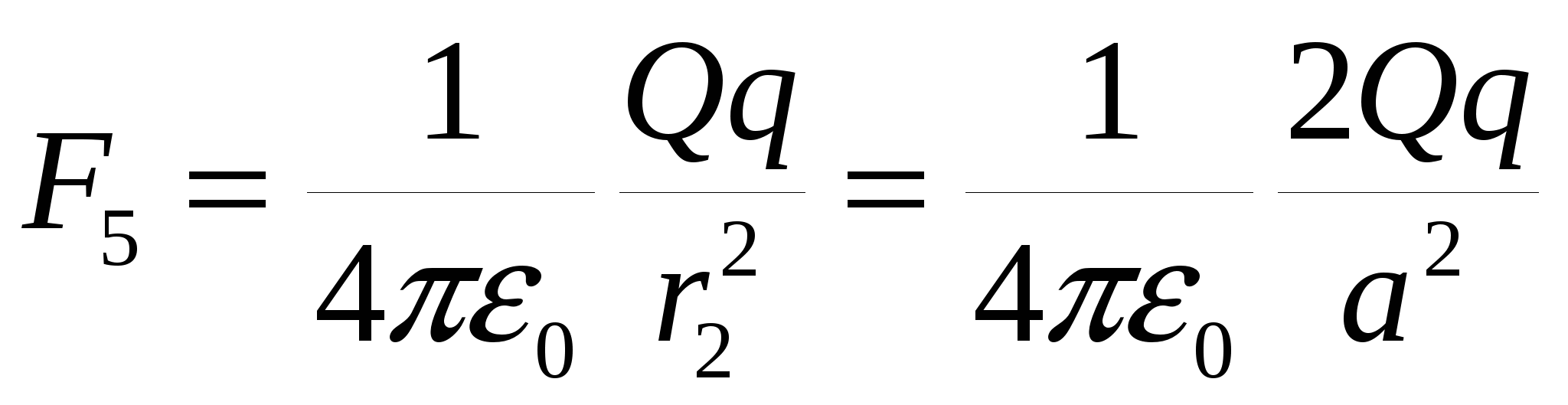 (2), где а - сторона квадрата, r1 - диагональ квадрата, r2 - половина диагонали. (2), где а - сторона квадрата, r1 - диагональ квадрата, r2 - половина диагонали.
Подставляя формулы (2) в (1), получаем уравнение:
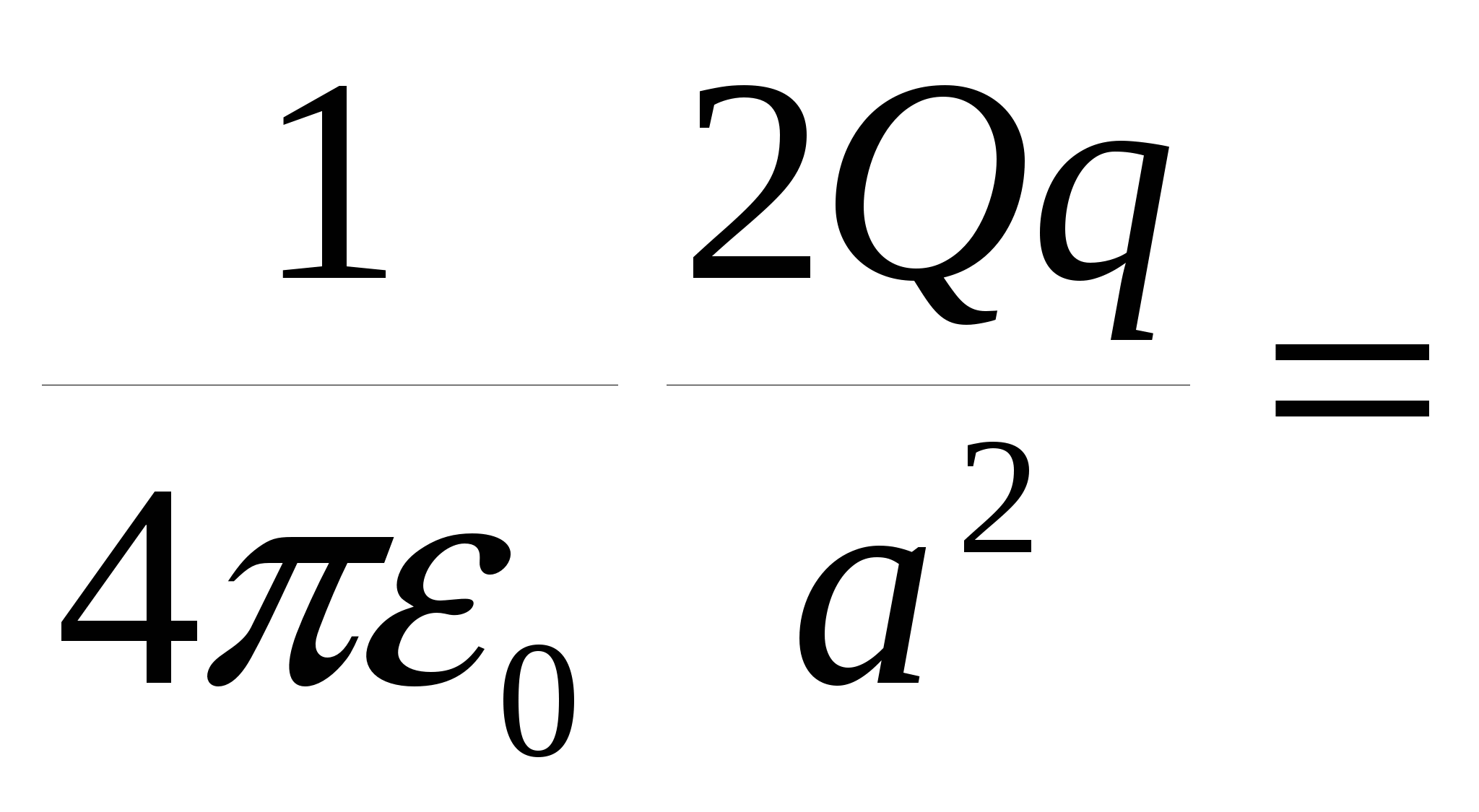 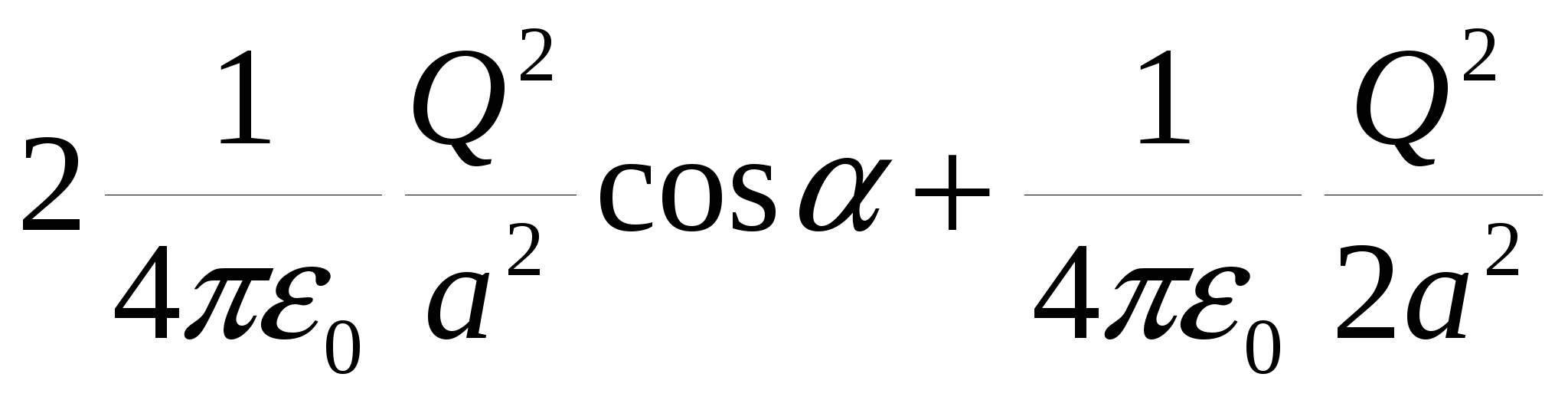 ; ;
откуда 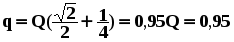 нКл нКл
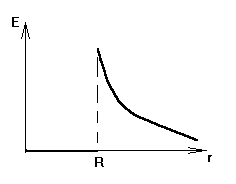
На металлической сфере радиусом R=12 см находится заряд Q=1 нКл. Определить напряженность электрического поля на расстоянии : 1) 8 см от центра; 2) на поверхности сферы; 3) на расстоянии 15 см от центра. Построить график зависимости E(r).
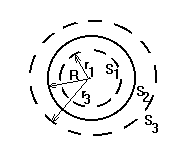
Для определения напряженности в области Е1 на расстоянии r1=8 см от центра сферы построим сферическую поверхность S1 радиусом r1. По теореме Гаусса-Остроградского:
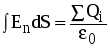 , ,
где Еn -нормальная составляющая напряженности электрического поля. Т.к. внутри сферы S1 зарядов нет, то 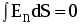 . Из соображений симметрии Еn=Е1=const, поэтому ее можно вынести за знак интеграла: . Из соображений симметрии Еn=Е1=const, поэтому ее можно вынести за знак интеграла: 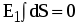 . Т.к. площадь сферы не равна нулю, то Е1=0. Напряженность во всех точках сферы, удовлетворяющих условию r1 . Т.к. площадь сферы не равна нулю, то Е1=0. Напряженность во всех точках сферы, удовлетворяющих условию r1
Для определения напряженности Е2 на поверхности сферы запишем теорему Гаусса-Остроградского:
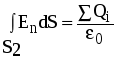 , ,
Из симметрии Еn=Е2=const и т.к. Qi=Q, можем записать:
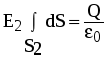 , подставляя площадь сферы, находим , подставляя площадь сферы, находим 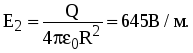
Для определения напряженности в области Е3 на расстоянии r3=15 см от центра сферы построим сферическую поверхность S3 радиусом r3. По теореме Гаусса-Остроградского:
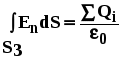 , ,
Из симметрии Еn=Е3=const и т.к. сумма зарядов внутри поверхности S3 равна Q, можем записать:
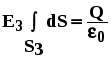 , подставляя площадь сферы S3, находим , подставляя площадь сферы S3, находим 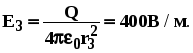
График зависимости Е(r):
На схеме сопротивление R=1,4 Ом, электродвижущие силы Е1=Е2=2 В, внутренние сопротивления этих элементов r1=1 Ом, r2=1,5 Ом. Найти силу тока в каждом из элементов и во всей цепи.
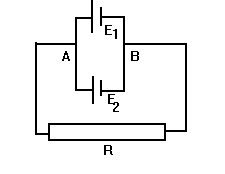
 В соответствии со вторым законом Кирхгофа для контура АЕ1ВЕ2А можем записать: В соответствии со вторым законом Кирхгофа для контура АЕ1ВЕ2А можем записать:
I1r1 - I2r2 = E1 -E2 (1)
по условию: E1 =E2 (2)
По первому закону Кирхгофа для узла В:
I1 + I2 = I (3)
и по второму закону Кирхгофа для контура AE2BA:
E2 = I2r2 + IR (4)
Подставляя значение I из уравнения (3) в (4), получим
E2 = I2r2 + (I1+ I2) R, откуда
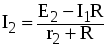
Подставив значение I2 в уравнение (1) и решая совместно (1) и (2), находим
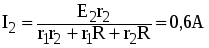
а затем 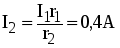 и и 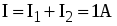
1. Закон Кулона
Сила гравитационного притяжения двух водяных одинаково заряженных капель радиусом 0,1 мм уравновешивается кулоновской силой отталкивания. Определить заряд капель. Плотность воды равна 1 г/см3.
Два заряженных шарика, подвешенных на нитях одинаковой длины, опускаются в керосин плотностью 0,8 г/см3. Какова должна быть плотность материала шариков, чтобы угол расхождения нитей в воздухе и керосине был один и тот же? Диэлектрическая проницаемость керосина =2.
В вершинах равностороннего треугольника находятся одинаковые положительные заряды Q=2 нКл. Какой отрицательный заряд Q1 необходимо поместить в центр треугольника, чтобы сила притяжения с его стороны уравновесила силы отталкивания положительных зарядов?
В центр квадрата, в каждой вершине которого находится заряд q=2,33 нКл, помешен отрицательный заряд q0. Найти этот заряд, если на каждый заряд q действует результирующая сила F=0.
Два шарика одинакового радиуса и массы подвешены на нитях одинаковой длины так, что их поверхности соприкасаются. После сообщения шарикам заряда q=0,4 мкКл они оттолкнулись друг от друга и разошлись на угол 2=60. Найти массу каждого шарика, если расстояние от центра шарика до точки подвеса L=20 см.
Два шарика одинакового радиуса и массы подвешены на нитях одинаковой длины так, что их поверхности соприкасаются. Какой заряд q нужно сообщить шарикам, чтобы после расхождения шариков на некоторый угол сила натяжения нитей стала равной Т=89 мН? Расстояние от центра шарика до точки подвеса L=10 см, масса каждого шарика m=5 г.
Два шарика массой m=0,1 г каждый подвешены в одной точке на нитях длиной 20 см каждая. Получив одинаковый заряд, шарики разошлись так, что нити образовали между собой угол =60. Найти заряд каждого шарика.
Два одинаковых шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол . Шарики погружаются в масло плотностью 0=8x102 кг/м3. Определить диэлектрическую проницаемость масла, если угол расхождения нитей при погружении шариков в масло остается неизменным. Плотность материала шариков =1,6x103 кг/м3.
Даны два шарика массой m=1 г каждый. Какой заряд Q надо сообщить каждому шарику, чтобы сила взаимного отталкивания зарядов уравновесила силу взаимного притяжения шариков по закону тяготения Ньютона? Рассматривать шарики как материальные точки.
В элементарной теории атома водорода принимают, что электрон обращается вокруг ядра по круговой орбите. Определить скорость v электрона, если радиус орбиты r=53 пм, а также частоту n вращения электрона.
Расстояние между двумя точечными зарядами Q1=1 мкКл и Q2=-Q1 равно 10 см. Определить силу F, действующую на точечный заряд Q=1 мкКл, удаленный на r1=6 см от первого и на r2=8 см от второго зарядов.
В вершинах правильного шестиугольника со стороной а=10 см расположены точечные заряды Q, 2Q, 3Q, 4Q, 5Q, 6Q (Q=0,1 мкКл). Найти силу F, действующую на точечный заряд Q, лежащий в плоскости шестиугольника и равноудаленный от его вершин.
Два одинаковых заряженных шарика находятся на расстоянии 60 см. Сила отталкивания шаров равна 70 мкН. После того, как шары привели в соприкосновение и удалили друг от друга на прежнее расстояние, сила отталкивания возросла и стала равной 160 мкН. Вычислить заряды Q1 и Q2 , которые были на шарах до их соприкосновения. Диаметр шаров считать много меньшим расстояния между ними.
Два одинаковых проводящих заряженных шарика находятся на расстоянии 30 см. Сила притяжения шаров равна 90 мкН. После того, как шары привели в соприкосновение и удалили друг от друга на прежнее расстояние, они стали отталкиваться друг от друга с силой 160 мкН. Вычислить заряды Q1 и Q2, которые были на шарах до их соприкосновения. Диаметр шаров считать много меньшим расстояния между ними.
Два положительных точечных заряда Q и 4Q закреплены на расстоянии 60 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд Q1 так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения заряда возможны только вдоль прямой, проходящей через закрепленные заряды.
Три одинаковых заряда Q=1 нКл каждый расположены по вершинам равностороннего треугольника. Какой отрицательный заряд надо поместить в центре треугольника, чтобы его притяжение уравновесило силы взаимного отталкивания зарядов? Будет ли это равновесие устойчивым?
Два алюминиевых шарика радиусами 2 см и 1 см соединены легкой непроводящей нитью длиной 1 м. Шарики находятся на гладкой горизонтальной непроводящей поверхности. У каждых z=109 атомов большего шарика взято по одному электрону и все они перенесены на меньший шарик. Какую минимальную силу нужно приложить к меньшему шарику, чтобы нить натянулась? Плотность и молярная масса алюминия равны соответственно =2,7x103 кг/м3 и =2,7x10-2 кг/моль, заряд электрона е=1,6x10-19 Кл.
С какой силой будут притягиваться два одинаковых свинцовых шарика диаметром 1 см, расположенные на расстоянии 1 м друг от друга, если у каждого атома первого шарика отнять по одному электрону и все эти электроны перенести на второй шарик?
На двух одинаковых каплях масла радиусом 8,22x10-3 см находятся одинаковые одноименные заряды. Определите их модуль, если сила кулоновского отталкивания уравновешивает силу притяжения капель. Расстояние между каплями гораздо больше их линейных размеров.
Два маленьких заряженных шарика, одинаковые по размеру, притягиваются друг к другу с некоторой силой. После того как шарики были приведены в соприкосновение и раздвинуты на расстояние в n раз большее, чем прежде, сила взаимодействия между ними уменьшилась в m раз. Каков был заряд первого шарика до соприкосновения, если второй шарик имел заряд q.
Три одинаковых заряда, каждый из которых равен q, расположены в вершинах равностороннего треугольника. Где и какой заряд надо поместить, чтобы система находилась в равновесии.
Четыре маленьких шарика соединены тонкими непроводящими нитями, так что в растянутом состоянии нити образуют ромб. Чему равен угол между нитями, если шарики, находящегося в противоположных вершинах ромба, имеют заряды Q1=Q2=Q, q1=q2=q.
Заряженные шарики, находящиеся на расстоянии 2 м друг от друга, отталкиваются с силой 1 Н. Общий заряд шариков 5x10-5Кл. Как распределен этот заряд между шариками?
Два маленьких, одинаковых по размеру заряженных шарика, находящиеся на расстоянии 0,2 м, притягиваются с силой 4x10-3Н. После того, как шарики были приведены в соприкосновение и затем разведены на прежнее расстояние, они стали отталкиваться с силой 2,25x10-3Н. Определить первоначальные заряды шариков.
На двух одинаковых капельках находится по одному лишнему электрону, причем сила электрического отталкивания капелек уравновешивает силу их взаимного тяготения. Каковы радиусы капелек.
Три маленьких шарика массой по 10 г каждый подвешены на шелковых нитях длиной по 1 м, сходящихся наверху в одном узле. Шарики одинаково заряжены и висят в вершинах равностороннего треугольника со стороной 0,1м. Каков заряд каждого шарика?
|
|
|
 Скачать 0.92 Mb.
Скачать 0.92 Mb.

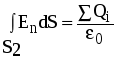 ,
,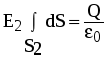 , подставляя площадь сферы, находим
, подставляя площадь сферы, находим 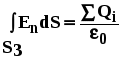 ,
,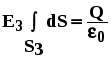 , подставляя площадь сферы S3, находим
, подставляя площадь сферы S3, находим 

