Электромагнетизм_задачи. Закон Кулона, где f сила взаимодействия двух точечных зарядов q 1 и q 2 в вакууме, r расстояние между зарядами

• Название: Закон Кулона, где f сила взаимодействия двух точечных зарядов q 1 и q 2 в вакууме, r расстояние между зарядами
• Анкор: Электромагнетизм_задачи.doc
• Дата: 30.10.2017
• Размер: 0.92 Mb.
• Имя файла: Электромагнетизм_задачи.doc
• Тип: Закон; #9963
• страница: 2 из 6

2. Энергия и потенциал точечного заряда.

1. 
   В вершинах квадрата со стороной 5 см находятся одинаковые положительные заряды Q=2 нКл. Определить напряженность электростатического поля: 1) в центре квадрата; 2) в середине одной из сторон.
   
2. 
   Расстояние L между зарядами Q=±2 нКл равно 20 см. Определить напряженность Е поля, созданного этими зарядами в точке, находящейся на расстоянии r₁=15 см от первого и r₂=10 см от второго заряда.
   
3. 
   Определить напряженность поля, создаваемого диполем с электрическим моментом р=10^-9 Кл•м на расстоянии r=25 см от центра диполя в направлении, перпендикулярном оси диполя.
   
4. 
   Два точечных заряда Q₁=4 нКл и Q₂=-2 нКл находятся на расстоянии 60 см друг от друга. Определить напряженность Е поля в точке, лежащей посередине между зарядами. Чему равна напряженность, если второй заряд положительный?
   
5. 
   Свинцовый шарик (=11,3 г/см³) диаметром 0,5 см помещен в глицерин (=1,26 г/см³). Определить заряд шарика, если в однородном электростатическом поле шарик оказался взвешенным в глицерине. Электростатическое поле направлено вертикально вверх, и его напряженность Е=4 кВ/см.
   
6. 
   Расстояние d между двумя точечными зарядами Q₁ =8 нКл и Q₂=-5,3 нКл равно 40 см. Вычислить напряженность Е поля в точке, лежащей посередине между зарядами. Чему равна напряженность, если второй заряд будет положительным?
   
7. 
   Электрическое поле создано двумя точечными зарядами Q₁=10 нКл и Q₂=-20 нКл, находящимися на расстоянии 20 см друг от друга. Определить напряженность Е поля в точке, удаленной от первого заряда на 30 см и от второго на 50 см.
   
8. 
   Расстояние d между двумя точечными положительными зарядами Q₁ =9Q и Q₂=Q равно 8 см. На каком расстоянии r от первого заряда находится точка, в которой напряженность Е поля зарядов равна нулю? Где находилась бы эта точка, если бы второй заряд был отрицательным?
   
9. 
   Расстояние между двумя точечными зарядами Q₁ =2Q и Q₂=-Q равно d. Найти положение точки на прямой, проходящей через эти заряды, напряженность Е поля в которой равна нулю.
   
10. 
    Электрическое поле создано двумя точечными зарядами Q₁=40 нКл и Q₂=-10 нКл, находящимися на расстоянии 10 см друг от друга. Определить напряженность Е поля в точке, удаленной от первого заряда на 12 см и от второго на 6 см.
    
11. 
    Три одинаковых заряда, q=10^-9Кл каждый, расположены в вершинах прямоугольного треугольника с катетами а=40 см и b=30 см. Найти напряженность электрического поля, создаваемого всеми зарядами в точке пересечения гипотенузы с перпендикуляром, опущенным на не из вершины прямого угла.
    
12. 
    Определить напряженность Е электрического поля, создаваемого точечным зарядом Q=10 нКл на расстоянии 10 см от него. Диэлектрик - масло.
    
13. 
    Электрическое поле создано двумя точечными зарядами Q₁=30 нКл и Q₂=-10 нКл, находящимися на расстоянии 20 см друг от друга. Определить напряженность Е поля в точке, удаленной от первого заряда на 15 см и от второго на 10 см.
    
14. 
    Электрическое поле создано двумя точечными зарядами Q₁=2 нКл и Q₂=-3 нКл, находящимися на расстоянии 20 см друг от друга. Определить 1) напряженность Е; 2) потенциал  поля в точке, удаленной от первого заряда на 15 см и от второго на 10 см.
    
15. 
    В вершинах квадрата со стороной 15 см находятся одинаковые положительные заряды Q=3 нКл. Определить напряженность электростатического поля: 1) в центре квадрата; 2) в середине одной из сторон.
    
16. 
    Расстояние L между зарядами Q=±4 нКл равно 10 см. Определить напряженность Е поля, созданного этими зарядами в точке, находящейся на расстоянии r₁=10 см от первого и r₂=15 см от второго заряда.
    
17. 
    Определить напряженность поля, создаваемого диполем с электрическим моментом р=10^-9 Кл•м на расстоянии r=15 см от центра диполя в направлении, перпендикулярном оси диполя.
    
18. 
    Два точечных заряда Q₁=6 нКл и Q₂=-4 нКл находятся на расстоянии 30 см друг от друга. Определить напряженность Е поля в точке, лежащей посередине между зарядами. Чему равна напряженность, если второй заряд положительный?
    
19. 
    Какой угол с вертикалью составит нить, на которой висит шарик массы 25 мг, если поместить шарик в горизонтальное однородное электрическое поле с напряженностью 35 В/м, сообщив ему заряд 7 мкКл?
    
20. 
    В однородном электрическом поле с напряженностью 1МВ/м, направленной под углом 30 к вертикали, висит шарик массы 2 г, несущий заряд 10 нКл. Найти силу натяжения нити Т.
    
21. 
    Шарик массы 1 г подвешен на нити длины 36 см. Как изменится период колебаний шарика, если, сообщив ему положительный или отрицательный заряд нКл, поместить шарик в однородное электрическое поле с напряженностью 100 кВ/м, направленной вниз?
    
22. 
    Одинаковые по модулю, но разные по знаку заряды нКл расположены в вершинах равностороннего треугольника со стороной а=2 см. Найти напряженность Е в третьей вершине треугольника.
    
23. 
    В вершинах при острых углах ромба, составленного из двух равносторонних треугольников со стороной а, помещены одинаковые положительные заряды q₁=q₂=q. В вершине при одном из тупых углов ромба помещен положительный заряд Q. Найти напряженность Е в четвертой вершине ромба.
    
24. 
    В вершинах при острых углах ромба, составленного из двух равносторонних треугольников со стороной а, помещены одинаковые положительные заряды q₁=q₂=q. В вершине при одном из тупых углов ромба помещен отрицательный заряд Q. Найти напряженность Е в четвертой вершине ромба, в случае, когда >q.
    
25. 
    В вершинах при острых углах ромба, составленного из двух равносторонних треугольников со стороной а, помещены одинаковые положительные заряды q₁=q₂=q. В вершине при одном из тупых углов ромба помещен отрицательный заряд Q. Найти напряженность Е в четвертой вершине ромба, в случае, когда
26. 
    В вершинах при острых углах ромба, составленного из двух равносторонних треугольников со стороной а, помещены одинаковые положительные заряды q₁=q₂=q. В вершине при одном из тупых углов ромба помещен отрицательный заряд Q. Найти напряженность Е в четвертой вершине ромба, в случае, когда =q.
    

3. Напряженность и потенциал поля объемного заряда. Теорема Остроградского- Гаусса.

1. 
   На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1) используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=4, ₂=; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять =30нКл/м², r=1,5R; 3) построить график Е(r).
   

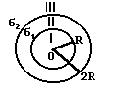2) На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=, ₂=-; 2)вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять =0,1мкКл/м², r=3R; 3)построить график Е(r).



3) На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-4, ₂=; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять =50нКл/м², r=1,5R; 3)построить график Е(r).



4) На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-2, ₂=; 2)вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять =0,1мкКл/м², r=3R; 3)построить график Е(r).



5) На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=2, ₂=; 2)вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять =40нКл/м², r=2R; 3)построить график Е(r).



6) На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-, ₂=; 2)вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять =10нКл/м², r=3R; 3)построить график Е(r).



7) На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=3, ₂=-6; 2)вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять =0,2мкКл/м², r=4R; 3)построить график Е(r).



8) На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-3, ₂=6; 2)вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять =0,3мкКл/м², r=3R; 3)построить график Е(r).



9) На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=6, ₂=; 2)вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора Е. Принять =0,3мкКл/м², r=1,5R; 3)построить график Е(r).



10) На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса и принцип суперпозиции электрических полей, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=2, ₂=; 2)вычислить напряженность Е в точке, расположенной слева от плоскостей , и указать направление вектора Е. Принять =0,1мкКл/м²; 3)построить график Е(x).



11) На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса и принцип суперпозиции электрических полей, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-4, ₂=2; 2)вычислить напряженность Е в точке, расположенной между плоскостями, и указать направление вектора Е. Принять =40нКл/м²; 3)построить график Е(x).



12) На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса и принцип суперпозиции электрических полей, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=4, ₂=-2; 2)вычислить напряженность Е в точке, расположенной справа от плоскостей , и указать направление вектора Е. Принять =20нКл/м²; 3)построить график Е(x).



13) На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса и принцип суперпозиции электрических полей, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-4, ₂=; 2)вычислить напряженность Е в точке, расположенной слева от плоскостей , и указать направление вектора Е. Принять =0,1мкКл/м²; 3)построить график Е(x).



14) На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса и принцип суперпозиции электрических полей, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=4, ₂=; 2)вычислить напряженность Е в точке, расположенной между плоскостями, и указать направление вектора Е. Принять =40нКл/м²; 3)построить график Е(x).



15) На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса и принцип суперпозиции электрических полей, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-, ₂=; 2)вычислить напряженность Е в точке, расположенной справа от плоскостей , и указать направление вектора Е. Принять =10нКл/м²; 3)построить график Е(x).



16) На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса и принцип суперпозиции электрических полей, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=3, ₂=-6; 2)вычислить напряженность Е в точке, расположенной слева от плоскостей, и указать направление вектора Е. Принять =0,2 мкКл/м²; 3)построить график Е(x).



17) На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса и принцип суперпозиции электрических полей, найти зависимость Е(x) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-3, ₂=6; 2)вычислить напряженность Е в точке, расположенной между плоскостями, и указать направление вектора Е. Принять =0,3 мкКл/м²; 3)построить график Е(x).



18) На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-2, ₂=; 2)вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять =50нКл/м², r=1,5R; 3)построить график Е(r).



19) На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=, ₂=-; 2)вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять =60нКл/м², r=3R; 3) построить график Е(r).



20) На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-, ₂=4; 2)вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять =30нКл/м², r=4R; 3)построить график Е(r).



21) На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=-2, ₂=4; 2)вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять =10нКл/м², r=3R; 3)построить график Е(r).



22) На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=, ₂=-3; 2)вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять =15нКл/м², r=2R; 3)построить график Е(r).



23) На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=4, ₂=3; 2)вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять =30нКл/м², r=5R; 3)построить график Е(r).



24) На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=3, ₂=; 2)вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять =10нКл/м², r=2R; 3)построить график Е(r).



25) На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями ₁ и ₂ (см. рис.). Требуется: 1)используя теорему Остроградского- Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, III. Принять ₁=6, ₂=-4; 2)вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора Е. Принять =20нКл/м², r=3R; 3)построить график Е(r).



26) Разность потенциалов между двумя коаксиальными бесконечными цилиндрами радиусами R₁=3см и R₂=10см, заряженными разноименными зарядами, равна U=450в. Определить: 1)заряд на единице длины цилиндров 2) плотность зарядов на каждом цилиндре 3)напряженность Е вблизи поверхности внутреннего цилиндра, на середине расстояния между цилиндрами и вблизи поверхности внешнего цилиндра.