Теория вероятностей и математическая статистика. Закон распределения случайной величины. Математическое ожидание 28 Дисперсия случайной величины 32
 Скачать 361.49 Kb.
|
ОглавлениеОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ 2 Случайные события 2 Вероятность событий 10 Условная вероятность. Независимость событий 15 Перестановки и сочетания 19 Формулы Байеса и полной вероятности 24 Дискретные случайные величины 27 Закон распределения случайной величины. Математическое ожидание 28 Дисперсия случайной величины 32 Биномиальное распределение 36 Плотность и функция распределения. Непрерывные случайные величины 39 Равномерное распределение непрерывной случайной величины 44 Нормальное распределение 47 МАТЕМАТИЧЕСКАЯ СТАТИСТИКА 53 Вариационные ряды 53 Графическое представление вариационных рядов 55 Показатели вариации 56 Средние вариационного ряда 56 Оценки разброса 59 Статистическое оценивание параметров 63 Выборочные оценки параметров генеральной совокупности 63 Свойства статистических оценок 64 Точечные и интервальные оценки 66 Проверка статистических гипотез 67 Функция Лапласа (таблица значений) 74 ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙДо сих пор мы рассматривали детерминированные математические модели, в которых ситуация характеризовалась полной определенностью (все условия были заданы и однозначно определяли результат). На практике это имеет место отнюдь не всегда, поскольку в реальной экономической ситуации обычно присутствует элемент неопределенности. Чтобы отразить этот элемент, строят стохастические, или вероятностные, математические модели (при этом за основу построения часто берется детерминированный вариант). В таких моделях используются средства теории вероятностей и математической статистики. Случайные событияПервоначальным понятием в теории вероятностей является понятие элементарного события. Множество (пространство) элементарных событий включает в себя все возможные взаимоисключающие исходы опыта (в экономике - некоторой экономической ситуации). Например, если опыт – подбрасывание монеты один раз, то пространство элементарных событий включает в себя два исхода – выпадение герба (Г) и выпадение решки (Р). Если монету бросают два раза, то пространство элементарных событий будет включать четыре исхода: ГР (вначале выпал герб, а потом решка), ГГ, РР и РГ. Если в том же опыте (двукратное бросание монеты) не важен порядок, в котором монета выпадала той или иной стороной, в качестве исходов можно рассматривать число выпадений, например, решки. Тогда исхода будет три – решка выпала 0, 1 или 2 раза. Другой пример - работа телефонной станции в течение некоторого промежутка времени, в качестве исходов рассматривается число поступивших вызовов от абонентов. Это может быть 0 вызовов, 1, 2 вызова и т.д. Здесь пространством элементарных событий является 0 и все множество натуральных чисел. Исходов бесконечно много. Другой пример – попадание на плоскость произвольной точки. Здесь тоже бесконечно много исходов (любая точка плоскости – элементарный исход). Случайное событие – любое подмножество пространства элементарных событий. Например, обозначим А – случайное событие, состоящее в том, что на телефонную станцию не поступит ни одного вызова, В – что поступит от 1 до 5 вызовов, С – от 6 до 20, D - не менее 3 вызовов. Случайное событие А включает в себя всего один исход (0), событие В – исходы 1, 2, 3, 4 и 5, событие С – 15 исходов из пространства элементарных событий, D - все исходы, кроме 0, 1 и 2. В примере с попаданием на плоскость произвольной точки тоже можно обозначить случайные события. Например, событие S1 состоит в том, что точка попала в квадрат (см. рисунок 1). Соответствующее подмножество будет включать все точки внутри и на границе этого квадрата. S1 Рисунок 1 – Случайное событие S1 состоит в том, что точка попала в квадрат Сумма событий – событие, состоящее в том, что произошло по крайней мере одно из событий, входящих в сумму (объединение соответствующих множеств): А + В = А 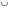 В.Можно сказать, что знак суммы в реальной жизни соответствует слову “или” - произошло одно из событий, входящих в сумму, или другое, или третье и т.д., или два или более одновременно. Например, событие А + В означает, что поступило не более пяти вызовов. Событие А + D означает, что вызовов либо не было, либо поступило не менее трех (все пространство элементарных событий, кроме 1 и 2 вызовов). Событие С + D = D, так как событие С представляет собой подмножество D (если произошло С, т.е. поступило от 6 до 20 вызовов, то D тем более произошло). Иначе говорят, что С влечет за собой D, или С D. Другой пример – если событие S2 состоит в том, что точка попала в круг, изображенный на рисунке 2, то событие S1 + S2 будет включать в себя все точки внутри и на границе области, выделенной на этом рисунке (точка попала либо в круг, либо в квадрат). S2 S1 Рисунок 2 – Событие S1 + S2 Произведение событий – событие, состоящее в том, что произошло каждое из событий, входящих в произведение (пересечение соответствующих множеств): А*В = А 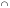 В.На практике это понятие соответствует слову “и” - произошло и одно событие, и другое, и все остальные. Например, событие В*D означает, что поступило от 3 до 5 вызовов (одновременно в интервале от 1 до 5 и не менее 3). Событие С*D = С, тоже так как событие С представляет собой подмножество D (количество вызовов должно быть не менее трех и одновременно от 6 до 20 вызовов – это и означает, что оно должно быть от 6 до 20). Другой пример – если событие S2 состоит в том, что точка попала в круг на рисунке 3, то событие S1*S2 будет включать в себя все точки внутри и на границе области, выделенной на этом рисунке (точка попала и в круг, и в квадрат одновременно). S2 S1 Рисунок 3 – Событие S1*S2 Событие, включающее в себя все пространство элементарных событий, называют достоверным (обозначим его 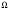 («омега»)), а пустое множество – невозможным событием.События называют несовместными, если их произведение является невозможным событием. Например, несовместны события А и В, так как если вызовы не поступали, их число не могло оказаться в интервале от 1 до 5: А*В =  .Другой пример – если событие S3 состоит в том, что точка попала в треугольник на рисунке 4, то события S1 и S3 будут несовместны, так как нет точек, попадающих одновременно в S1 и в S3 (нельзя одновременно попасть в области, ограниченные квадратом и треугольником), т.е. S1*S3 = . S2 S3 S1 Рисунок 4 – События S1 и S3 несовместны Событие называют противоположным другому событию, если они несовместны, а их сумма достоверна. Событие, противоположное А, обозначают 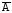 .  .Например, для нашего примера событие 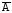означает, что вызовы поступали (противоположность тому, что их не было). При этом А*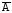 =  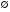(если вызовы поступали, их число не равно 0), а событие А + 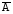 достоверно (можно с уверенностью утверждать, что вызовы либо поступали, либо нет). 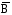Событие  означает, что вызовов либо не было, либо было более 5.При формулировке противоположного события следует проявлять внимательность. Например, события “вызовы были” и “вызовов не было” действительно, противоположны, в чем мы только что убедились. А вот события “все изделия в партии бракованные” и “все изделия в партии не содержат брака” противоположными не являются. В самом деле, хотя они и несовместны, но их сумма вовсе не является достоверной (не обязательно все изделия должны быть бракованными или все доброкачественными, - возможно, что часть из них содержит брак, а часть нет). Событием, противоположным событию “все изделия бракованные”, является событие “не все изделия бракованные” (или, что то же самое, “хотя бы одно изделие не бракованное”). Событием, противоположным событию “все изделия не содержат брака”, является событие “хотя бы одно изделие содержит брак”. В примере с попаданием на плоскость произвольной точки событие  , изображенное выделением на рисунке 5, состоит в том, что точка попала в любую точку плоскости, за исключением точек внутри и на границе квадрата. S1 Рисунок 5 – События S1 и противоположныМожно доказать, что выполняются следующие свойства операций сложения и умножения (свойства (3) и (4) проиллюстрированы графически на рисунках 6-9): 1) А + В = В + А; АВ = ВА – коммутативность; 2) А + (В + С) = (А + В) + С; (АВ)С = А(ВС) – ассоциативность; 3) (А + В)*С = А*С + В*С (см. рисунок 6); А + ВС = (А + В)(А + С) – дистрибутивность (см. рисунок 7); 4) 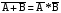 (см. рисунок 8);  (см. рисунок 9);5) для любого события А верно А*А = А; А + А = А. S2 S1 S4 Рисунок 6 – S1(S2 + S4) = S1S2 + S1S4 S2 S1 S4 Рисунок 7 – S1 + S2*S4 = (S1 + S2)*(S1 + S4) S2 S1 S2 S1 Рисунок 8 –  Рисунок 9 – 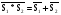 Разностью двух событий называют событие, состоящее в том, что первое из них произошло, а второе не произошло: А - В= 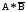 .Для примера с телефонной станцией событие (D – С) означает, что поступило либо от 3 до 5 вызовов, либо более 20 (т.е. не менее трех, но не от 6 до 20). Событие (D – В) означает, что поступило более 5 вызовов (не менее трех, но не от 1 до 5). В примере с попаданием на плоскость произвольной точки событие (S1 - S2) будет включать в себя все точки внутри и на границе области, выделенной на рисунке 10 (точка попала в квадрат, но не в круг). S2 S1 Рисунок 10 – Событие S1 - S2 |