Теория вероятностей и математическая статистика. Закон распределения случайной величины. Математическое ожидание 28 Дисперсия случайной величины 32
 Скачать 361.49 Kb. Скачать 361.49 Kb.
|
Перестановки и сочетанияЧислом сочетаний из n по m (Cmn) называют число всех различных m–элементных подмножеств n–элементного множества (различными множествами считаются те, которые имеют различный состав элементов, порядок отбора при этом не важен). Во многих стохастических задачах возникает необходимость в определении числа сочетаний. Чтобы получить общую формулу для числа сочетаний, определим вначале вероятность того, что будет получено одно конкретное сочетание. В соответствии с классическим определением вероятности эта вероятность будет величиной, обратной числу сочетаний (так как оно равно числу элементарных событий). Итак, определим вероятность того, что будет выбрано m конкретных элементов из n (например, из n шаров, m из которых черные, будут выбраны именно эти m черных шаров). Вероятность того, что первый элемент будет выбран из этого подмножества, равна m/n. Условная вероятность того, что второй элемент будет выбран из него же, равна (m-1)/(n-1), и т.д. Вероятность сочетания отсюда будет равна 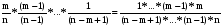 . .В числителе полученной формулы стоит m!. Если бы в знаменателе перемножались числа от 1 до n, то мы получили бы n!. Однако, сомножителей в знаменателе меньше, поскольку числа от 1 до (n – m) в это произведение не входят. Значит, n! надо разделить на (n – m)!: 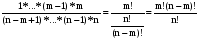 . .Отсюда обратная величина 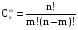 . .Так, 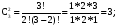 В самом деле, например, из трех букв А, В и С можно составить 3 2-хбуквенных сочетания: АВ, ВС и АС; и только одно 3-хбуквенное – АВС. Вернемся к примеру о формировании подкомитета из трех человек в совете директоров, который состоит из трех бухгалтеров, трех менеджеров и двух инженеров. Вероятность того, что подкомитет будет полностью состоять из бухгалтеров (обозначим это событие D), теперь можно подсчитать по-другому. Числу элементарных событий будем теперь рассматривать, как число сочетаний по три человека из 8 членов совета. Событие D представляет собой все сочетания по три человека из трех бухгалтеров. Определим искомую вероятность: Р(D) = 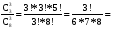 1/56 (результат совпадает с полученным ранее). 1/56 (результат совпадает с полученным ранее).До введения понятия сочетания мы получили результат 1/56, как вероятность произведения трех зависимых событий (что первым в подкомитет выбран бухгалтер, вторым – бухгалтер, и третьим – тоже бухгалтер) - 3/8*2/7*1/6. При использовании другого подхода решение существенно не упростилось. Немного изменим условия задачи – пусть теперь подкомитет формируется из четырех человек. Определим вероятность того, что в нем будут трое бухгалтеров (обозначим теперь это событие D). Вначале не будем использовать формулы для числа сочетаний. Одним из вариантов, когда будет иметь место D, является событие, когда первыми тремя в подкомитет выбраны бухгалтера. Эта вероятность уже подсчитана (3/8*2/7*1/6; четвертым в подкомитет может быть выбран любой из оставшихся директоров). Однако, D будет иметь место и в том случае, если не бухгалтер выбран в подкомитет, например, вторым, а не четвертым: вероятность события, что бухгалтера выбраны первым, третьим и четвертым, равна 3/8*5/7*2/6*1/5. Кроме того, не бухгалтер может быть выбран первым или третьим: вероятности соответственно 5/8*3/7*2/6*1/5 и 3/8*2/7*5/6*1/5. Событие D представляет собой сумму этих четырех несовместных событий: Р(D) = 3/8*2/7*1/6 + 3/8*5/7*2/6*1/5 + 5/8*3/7*2/6*1/5 + 3/8*2/7*5/6*1/5 = (3*2*4)/(6*7*8) = 1/14. Определить эту вероятность с помощью формул для числа сочетаний. Числу элементарных событий - число сочетаний по 4 человека из 8 директоров. Число элементарных событий в событии D можно определить как число сочетаний по три человека из трех бухгалтеров, умноженное на число сочетаний по одному человеку из оставшихся пяти: С33*С15 = 5. Тогда Р(D) = = 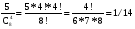 . .Более сложные практические задачи решить без использования сочетаний становится уже довольно сложно. Рассмотрим другой пример, решение которого существенно упрощается при использовании понятия сочетания. Из трех бухгалтеров, восьми менеджеров и шести инженеров случайным отбором формируется комитет из 10 человек. Определим вероятность того, что в него войдут 1 бухгалтер, 5 менеджеров и 4 инженеров. Вначале рассмотрим сочетания для бухгалтеров, менеджеров и инженеров в составе комитета по отдельности. Выбрать одного бухгалтера из трех можно 3 способами. Выбрать пять менеджеров из 8 можно 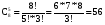 способами. И инженеров можно отобрать в комитет данного состава способами. И инженеров можно отобрать в комитет данного состава 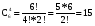 способами. Теперь можно определить, каким количеством способов можно сформировать комитет данного состава: С13*С58*С46 = 3*15*56. способами. Теперь можно определить, каким количеством способов можно сформировать комитет данного состава: С13*С58*С46 = 3*15*56.Общее число способов сформировать комитет равно 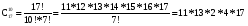 . .Теперь определим искомую вероятность 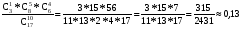 . .Числом перестановок из n по m (Рmn) называют число всех различных m–элементных выборок из n–элементного множества, причем элементы внутри них упорядочены (перестановки считаются различными, если элементы внутри них расположены в различном порядке). Как определить число перестановок? На первое место в перестановке могут попасть n элементов. На второе – n-1. Поэтому перестановку по 2 элемента из n можно составить n(n-1) способами. Рассуждая далее аналогично, перестановку по m элементов можно составить n*(n-1)*…*(n-m + 1) способами. Итак, 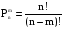 . .Так, Рассмотрим пример вычисления вероятности с помощью перестановок. Эксперт по маркетингу начал свою работу в фирме с составления прогноза о том, какие из 5 товаров, выпускаемых фирмой, будут пользоваться наибольшим спросом на рынке. Согласно этому прогнозу, из товаров А, В, С, D и Е наибольший успех ожидал товар Е, затем товар С, а затем В. О товарах А и D ничего сказано не было. Прогноз оправдался. Определить вероятность того, что это случайное совпадение. Казалось бы, число 3 не так уж велико по сравнению с пятью, и даже не изучая рыночную обстановку и товары, можно просто угадать, в каком порядке 3 из 5 товаров будут лидировать на рынке. Чтобы определить число элементарных событий, подсчитаем число перестановок по 3 из 5: 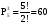 . Эксперт выбрал одну перестановку, и вероятность случайного успеха была 1/60 . Эксперт выбрал одну перестановку, и вероятность случайного успеха была 1/60 0,017. Эта величина достаточно мала, и мы можем считать, что эксперт действительно разбирается в рыночной ситуации. Однако, при большом числе таких экспериментов даже неквалифицированный человек может составить правильный прогноз. В среднем из 60 таких прогнозов 1 может оказаться правильным случайно. 0,017. Эта величина достаточно мала, и мы можем считать, что эксперт действительно разбирается в рыночной ситуации. Однако, при большом числе таких экспериментов даже неквалифицированный человек может составить правильный прогноз. В среднем из 60 таких прогнозов 1 может оказаться правильным случайно. |
