Теория вероятностей и математическая статистика. Закон распределения случайной величины. Математическое ожидание 28 Дисперсия случайной величины 32
 Скачать 361.49 Kb. Скачать 361.49 Kb.
|
Графическое представление вариационных рядовДля более наглядного представления временных рядов используют следующие виды графиков. 1. Полигон распределения представляет собой график частот. Это ломаная линия, абсциссы вершин которой соответствуют вариантам, а ординаты – частотам. Обычно его используют для дискретных вариационных рядов. На рисунке 17 представлен полигон распределения для вариационного ряда, приведенного в таблице 5. 2. Кумулята представляет собой график накопленных частот (ее еще называют кумулятивной кривой). На рисунке 17 представлена кумулята для того же самого ряда. Рисунок 17 – Полигон распределения и кумулята 3. График эмпирической функции распределения представляет собой график накопленных относительных частот, т.е. относительных частот того, что признак принял значение, меньшее заданного. Для примера из таблицы 5 он представлен на рисунке 18 (рекомендуется сравнить с графиком функции распределения, которая рассматривалась при изучении теории вероятностей). 4. Гистограмма распределения представляет собой фигуру, составленную из прямоугольников, каждый из которых соответствует интервалу сгруппированного ряда, а их высота равна соответствующим частотам. Для примера из таблицы 4 гистограмма распределения представлена на рисунке 19. Для сгруппированного ряда можно также построить полигон распределения (соединив отрезками середины верхних оснований прямоугольников гистограммы) и кумуляту (см. рисунок 19). Рисунок 18 – Эмпирическая функция распределения Рисунок 19 – Кумулята, полигон и гистограмма распределения для сгруппированного вариационного ряда Показатели вариацииСредние вариационного рядаОсновным показателем вариации называется среднее арифметическое вариационного ряда 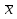 , которое рассчитывается по формуле: , которое рассчитывается по формуле: 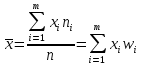 , ,где n – общее число наблюдений; m – число вариант; ni – частота варианты хi; wi – относительная частота варианты хi. Например, для таблицы 5 среднее арифметическое 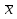 = (2*3 + 3* 25 + 4*39 + 5*33) = 4,02 (балла). = (2*3 + 3* 25 + 4*39 + 5*33) = 4,02 (балла).Свойства этой средней величины аналогичны свойствам математического ожидания. Кроме того, если вариационный ряд разбит на несколько групп, то среднее арифметическое всего ряда можно рассчитать, как среднее арифметическое групповых средних: 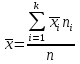 , ,где n – общее число наблюдений; k – число групп; 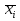 - среднее арифметическое i-й группы; - среднее арифметическое i-й группы;ni – число наблюдений в i-й группе. Например, если среди ста студентов, оценки которых приведены в таблице 5, присутствуют студенты двух различных специальностей, то можно разбить этот вариационный ряд на две группы (см. таблицы 7 и 8). По данным второго и третьего столбцов этих таблиц можно рассчитать средний балл для студентов специальности № 1 (он составил 4,12 балла) и средний балл для студентов специальности № 2 (он составил 3,875 балла). Теперь для расчета общей средней можно воспользоваться вышеприведенной формулой: (4,12*60 + 3,875*40) /100 = 4,02 (балла), - что совпадает с полученным ранее результатом. Если всех студентов, данные о которых приведены в таблице 5, выстроить в ряд по возрастанию полученного ими балла, то из этих ста человек в середине стояли бы студенты под номерами 50 и 51 от начала ряда. Оба эти студента получили оценку 4, так как накопленная частота для оценки 3 составляет 28, а для оценки 4 она составляет 67 (все студенты под номерами с 29-го по 67-й включительно получили оценку 4). То значение варианты, которое соответствует середине вариационного ряда, называется медианой и обозначается Me. Если число наблюдений – нечетное, то медианный номер равен (n + 1)/2; а если четное – то медианных номеров два: n/2 и ((n/2) +1), а сама медиана рассчитывается, как среднее арифметическое этих двух вариант. В примере из таблицы 5 медианные номера 50 и 51, а Me = (4 + 4)/2 = = 4 (балла). Та варианта, которая встречается в вариационном ряду чаще всего, называется модой (мода – это то значение признака, которое встречается у большинства наблюдений) и обозначается Mo. В таблице 5 Mo = 4 (балла), так как этой варианте соответствует наибольшая частота 39. Для интервального вариационного ряда используется несколько более сложная методика расчета рассмотренных средних, которую здесь рассматривать не будем. В вышеприведенном примере Мо = Ме = 4 4,02 = 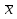 . Это отнюдь не всегда бывает так. Например, если рассчитать средние по данным таблицы 6, то можно получить . Это отнюдь не всегда бывает так. Например, если рассчитать средние по данным таблицы 6, то можно получить 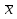 = 3,81 4, Me = 3, Mo = 5. Т.е. при том, что большинство студентов получили 5 (42 человека), в середине ряда оказались студенты с оценкой 3, а средний балл составил чуть меньше 4. = 3,81 4, Me = 3, Mo = 5. Т.е. при том, что большинство студентов получили 5 (42 человека), в середине ряда оказались студенты с оценкой 3, а средний балл составил чуть меньше 4.Таблица 6 – Дискретный вариационный ряд
Оценки разбросаДля оценки разброса значений вариационного ряда используются показатели размаха, отклонений и коэффициента вариации. Размах вариации представляет собой разность между наибольшим и наименьшим значениями вариант. Например, для таблицы 4 размах R составил R = 5 – 2,5 = 2,5 (балла). Для таблиц 5 и 6 R = 5 – 2 = 3 (балла). Среднее линейное отклонение представляет собой среднее арифметическое модулей отклонений вариант от своего среднего арифметического; рассчитывается по формуле: 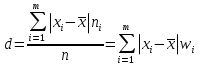 Для примера из таблицы 5 d = (|2 – 4,02|*3 + |3 – 4,02|*25 + + |4 – 4,02|*39 + |5 – 4,02|*33)/100 = 0,6468 (балла), т.е. в среднем оценка студента отличается от среднего балла примерно на 0,6 балла. Отметим, что если в этой формуле убрать знак модуля, то отклонения в разные стороны компенсируют друг друга, и результат окажется равным нулю (по соответствующему свойству среднего арифметического, аналогичного свойству математического ожидания). Если вместо взятия по модулю возвести отклонение в квадрат, получим дисперсию вариационного ряда 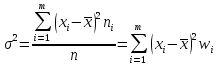 . .Для примера из таблицы 5 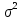 = 0,6996. Единицы измерения этой величины (баллы в квадрате) не имеют смысла, поэтому из нее извлекают корень квадратный и получают среднеквадратическое отклонение. В том же примере = 0,6996. Единицы измерения этой величины (баллы в квадрате) не имеют смысла, поэтому из нее извлекают корень квадратный и получают среднеквадратическое отклонение. В том же примере 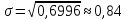 (балла). Столько составляет корень квадратный из среднего квадрата отклонения оценки каждого студента от среднего балла. (балла). Столько составляет корень квадратный из среднего квадрата отклонения оценки каждого студента от среднего балла.Свойства дисперсии для вариационного ряда аналогичны свойствам дисперсии в теории вероятностей. Для ее расчета можно вывести аналогичную формулу: 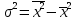 . .Кроме того, если ряд состоит из нескольких отдельных групп наблюдений (пусть их число равно k), то его дисперсию можно рассчитать по следующей формуле: 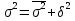 где 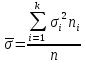 – средняя внутригрупповая дисперсия; – средняя внутригрупповая дисперсия; 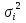 – дисперсия i-й группы; – дисперсия i-й группы; 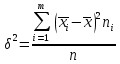 - межгрупповая дисперсия. - межгрупповая дисперсия.Чтобы проиллюстрировать это правило, вернемся к примеру, в котором данные из таблицы 5 разбиты на две (k = 2) группы и представлены в таблицах 7 и 8. Таблица 7– Оценки для специальности № 1
Рассчитаем групповую дисперсию для таблицы 7 по формуле 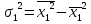 = 17,65 – 4,122 = 0,7. = 17,65 – 4,122 = 0,7.Таблица 8– Оценки для специальности № 2
Рассчитаем групповую дисперсию для таблицы 8 по формуле 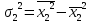 = 15,675 – 3,8752 = 0,66. = 15,675 – 3,8752 = 0,66.Сведем расчеты в таблицу 9: Таблица 8– Оценки для двух специальностей
Тогда межгрупповая дисперсия составит 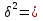 ((4,12 – 4,02)2*60 + (3,875 – 4,02)2*40)/100 = 0,01 ((4,12 – 4,02)2*60 + (3,875 – 4,02)2*40)/100 = 0,01Средняя внутригрупповых дисперсий составит 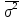 = (0,7*60 + 0,66*40)/100 = 0,68 = (0,7*60 + 0,66*40)/100 = 0,68Дисперсия всего вариационного ряда составит 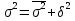 = 0,68 + = 0,68 ++ 0,01 = 0,69, что приблизительно совпадает с полученным ранее результатом. Незначительное расхождение объясняется погрешностью округления (при расчетах с помощью электронной таблицы совпадение получается точным). |

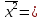 17,65
17,65