Теория вероятностей и математическая статистика. Закон распределения случайной величины. Математическое ожидание 28 Дисперсия случайной величины 32
 Скачать 361.49 Kb. Скачать 361.49 Kb.
|
Статистическое оценивание параметровВыборочные оценки параметров генеральной совокупностиПри составлении таблицы 5 были собраны данные об оценках ста студентов. При этом исследователя могут интересовать оценки не только этих ста студентов, но всех студентов вообще. Вся совокупность наблюдений, которые гипотетически существуют и подлежат изучению, называется генеральной совокупностью наблюдений. Та часть наблюдений, которая отбирается для осуществления статистических расчетов, называется выборочной совокупностью, или выборкой. Выборка обязательно должна правильно отражать основные свойства генеральной совокупности, которые интересуют исследователя, т.е. выборка должна быть репрезентативной. В нашем примере 100 студентов представляют собой выборку из генеральной совокупности всех студентов вообще. Число наблюдений в выборке называют объемом выборки. В нашем примере объем выборки n = 100. Выборку формируют двумя основными способами: бесповторным отбором (когда один и тот же элемент генеральной совокупности не может более одного раза встретиться в выборочной совокупности наблюдений) и повторным отбором (когда такое возможно). В нашем примере, если опрошенные 100 студентов – разные студенты, то выборка является бесповторной. Если бы оценку одного и того же студента можно было включить в выборку два и более раз, то выборка была бы повторной: у студента спрашивают, какую он получил оценку, записывают результат без фамилии, затем наугад спрашивают еще одного студента, и т.д. При этом может снова встретиться студент, который уже был опрошен. Отметим, что рассмотренные выше показатели могут иметь разные значения для выборки и для генеральной совокупности. Поэтому различают генеральную и выборочную средние, генеральную и выборочную дисперсии и т.п. При этом для одной и той же генеральной совокупности можно получить разные выборочные средние или дисперсии, если взять из нее разные выборки (т.е. для одной сотни студентов средний балл примет одно значение, для других ста студентов – другое и т.д.). Однако, по значениям выборочных показателей можно все же судить о значениях этих показателей для генеральной совокупности. Таким образом, те расчеты, которые мы осуществляем по выборочным данным, позволяют нам дать выборочную оценку параметров (показателей) генеральной совокупности. Свойства статистических оценокКачество получаемых оценок определяется следующими основными свойствами: 1) несмещенность - математическое ожидание оценки должно быть равно неизвестному истинному значению параметра. Это означает, что выборочные оценки как бы концентрируются вокруг неизвестных истинных значений параметров; не происходит систематических ошибок при оценивании. Это очень важное свойство, - если бы оно не выполнялось, оценка давала бы заведомо неверную информацию. 2) состоятельность – оценки должны удовлетворять закону больших чисел, т.е при стремлении числа наблюдений к бесконечности вероятность того, что отклонение выборочной оценки от истинного значения будет ничтожно малым, стремится к единице. Сущность закона больших чисел состоит в том, что при большом числе случайных величин их средний результат становится практически достоверным (совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая). На практике свойство состоятельности означает, что для получения достоверных оценок целесообразно брать большие по объему выборки. С ростом числа наблюдений разброс оценок становится все меньше, оценки становятся все более надежными, все плотнее концентрируются вокруг истинных значений. Т.е. если взять тридцать выборок по сто студентов, то будет получено тридцать выборочных оценок, для которых можно подсчитать дисперсию. Если взять тридцать выборок по двести студентов, то будут получены другие тридцать оценок, дисперсия которых, скорее всего, будет меньше. Если брать выборки по триста, по пятьсот, по тысяче студентов и т.д., то дисперсии, скорее всего, будут и далее уменьшаться. При стремлении числа наблюдений к бесконечности дисперсии оценок стремятся к нулю, т.е. оценки становятся почти равны истинным значениям. 3) эффективность – это свойство имеет место для несмещенных оценок, которые имеют наименьшую дисперсию по сравнению с любыми другими несмещенными оценками параметров по выборке того же объема. Можно доказать, что выборочная средняя всегда является несмещенной и состоятельной оценкой генеральной средней. Однако, для выборочной дисперсии будет выполняться только свойство состоятельности. Можно доказать, что выборочная дисперсия будет смещенной оценкой генеральной дисперсии, т.е. будет давать систематическую ошибку (причем в сторону уменьшения: генеральная дисперсия занижается). Чтобы исправить это, для расчета оценки генеральной дисперсии необходимо внести изменения в формулу, по которой рассчитывается выборочная дисперсия. А именно, сумму квадратов отклонений от среднего делят не на число наблюдений, а на это число минус единица: 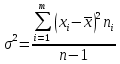 . Такая оценка будет несмещенной. . Такая оценка будет несмещенной.Вопросы эффективности оценок здесь рассматривать не будем. Точечные и интервальные оценкиЕсли оценка параметра представляет собой одно число, такую оценку называют точечной (это точка на числовой оси). Рассмотренные выше оценки являются точечными. Если при оценивании мы находим интервал значений, в который истинное значение попадает с некоторой вероятностью, то такая оценка будет интервальной. Соответствующий интервал называют доверительным интервалом, а вероятность – доверительной вероятностью (или надежностью). Например, пусть x – средний балл студента. Пример точечной оценки: 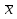 = 4,5. = 4,5.Пример интервальной оценки: 4,2 ≤ 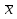 ≤ 4,8 (или, что то же самое, ≤ 4,8 (или, что то же самое, 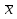 = 4,5 ± 0,3) с вероятностью 0,93. Другой пример интервальной оценки: = 4,5 ± 0,3) с вероятностью 0,93. Другой пример интервальной оценки: 4,1 ≤ 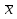 ≤ 4,9 с вероятностью 0,95 (т.е. ≤ 4,9 с вероятностью 0,95 (т.е. 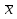 = 4,5 ± 0,4). = 4,5 ± 0,4). Следует обратить внимание, что чем больше берется доверительная вероятность, тем шире оказывается доверительный интервал. Собственно, в приведенном примере, даже не зная значение средней, можно точно сказать (с вероятностью 1), что 2 ≤ 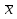 ≤ 5, так как других значений оценка в этой шкале принять вообще не может. Однако такая информация очевидно бесполезна для исследователя. Чем меньше берется доверительный интервал, тем больше вероятность ошибки, т.е. того, что мы в него не попадем (а доверительная вероятность, соответственно, меньше). Т.е. более точные оценки даются с меньшей вероятностью. ≤ 5, так как других значений оценка в этой шкале принять вообще не может. Однако такая информация очевидно бесполезна для исследователя. Чем меньше берется доверительный интервал, тем больше вероятность ошибки, т.е. того, что мы в него не попадем (а доверительная вероятность, соответственно, меньше). Т.е. более точные оценки даются с меньшей вероятностью.Итак, если границы доверительного интервала для значений некоторого параметра А определяются формулой А ± при доверительной вероятности , то чем больше , тем больше . Для определения используются формулы, вид которых зависит от того, какой параметр оценивается, каким методом, и выборка какого типа при этом используется. Кроме того, при расчете по этим формулам используется информация об объемах выборки и генеральной совокупности и о значении . Необходимые формулы можно найти в учебниках и справочниках по статистике. |
