Теория вероятностей и математическая статистика. Закон распределения случайной величины. Математическое ожидание 28 Дисперсия случайной величины 32
 Скачать 361.49 Kb. Скачать 361.49 Kb.
|
Формулы Байеса и полной вероятностиПусть Вi, P(Вi)>0, i = 1,n – попарно несовместные события, и если произошло некоторое событие А, то произошло и событие 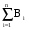 . Тогда . Тогда Р(А) = 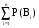 Р(А/Вi) – формула полной вероятности. Р(А/Вi) – формула полной вероятности.В самом деле, событие А можно представить, как сумму попарно несовместных событий А = АВ1 + АВ2 + . . . + АВn (ведь если произошло А, то хотя бы какое-нибудь из Вi тоже произошло): Р(А) = Р(АВ1 + АВ2 + . . . + АВn) = Р(АВ1) + Р(АВ2) + . . . + Р(АВn) = Р(В1)*Р(А/В1) + Р(В2)*Р(А/В2) + . . . + Р(Вn)*Р(А/Вn). По определению условной вероятности Р(Вi/А) = Р(АВi)/Р(А) = Р(Вi)*Р(А/Вi)/Р(А). Подставим в это выражение формулу полной вероятности: Р(Вi/А) = Р(Вi)*Р(А/Вi)/( 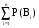 Р(А/Вi)). Р(А/Вi)).Полученное выражение – формула Байеса. Рассмотрим примеры использования полученных формул. Имеется три фирмы-поставщика деталей. На долю первой фирмы приходится 50% общего объема поставок, а на две другие – соответственно 30% и 20%. Из практики известно, что 10% деталей, поставляемых первой фирмой, - бракованные. Для второй и третьей фирм процент брака соответственно 5% и 6%. Из поставленных деталей наугад берется одна деталь. Определим 1) вероятность того, что эта деталь бракованная, и 2) вероятность того, что если деталь бракованная, она поставлена первой фирмой. Определим события следующим образом. Событие А – деталь бракованная, событие В1,– деталь получена от 1-й фирмы, события В2 и В3 – от 2-й и 3-й фирм соответственно. Тогда Р(В1) = 1/2 (50%); Р(В2) = 3/10; Р(В3) = 1/5; Р(А/В1) = 1/10; Р(А/В2) = 1/20; Р(А/В3) = 3/50. Нам необходимо определить Р(А) и Р(В1/А). Отметим, что если произошло событие А, то и событие (В1 + В2 + В3) тоже произошло. Событие (В1 + В2 + В3) вообще достоверно (Р(В1 + В2 + В3) = Р(В1) + Р(В2) + Р(В3) = 1), оно всегда будет иметь место, так как других поставщиков, кроме этих трех фирм, нет; деталь обязательно поставлена одной или другой из них. События В1, В2 и В3 попарно несовместны, так как деталь не может быть одновременно поставлена двумя разными фирмами. Следовательно, для определения Р(А) можно воспользоваться формулой полной вероятности: Р(А) = 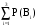 Р(А/Вi) = (1/2) * (1/10) + (3/10) * (1/20) + (1/5) * (3/50) = 1/20 + 3/200 + 3/250 = (50 + 15 + 12)/1000 = 0,077. Р(А/Вi) = (1/2) * (1/10) + (3/10) * (1/20) + (1/5) * (3/50) = 1/20 + 3/200 + 3/250 = (50 + 15 + 12)/1000 = 0,077.Для определения Р(В1/А) воспользуемся формулой Байеса: Р(В1/А) = Р(В1)*Р(А/В1)/( 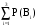 Р(А/Вi)). Выражение в знаменателе уже подсчитано – это Р(А). Р(В1/А) = (1/2)*(1/10)/0,077 = 50/77 Р(А/Вi)). Выражение в знаменателе уже подсчитано – это Р(А). Р(В1/А) = (1/2)*(1/10)/0,077 = 50/77 0,65. 0,65.Другой пример. В бухгалтерию поступают пачки накладных для проверки и обработки. 90% пачек были признаны удовлетворительными: они содержали только 1% неправильно оформленных накладных. Остальные 10% пачек были признаны неудовлетворительными, так как содержали 5% неправильно оформленных накладных. Определим 1) вероятность того, что если первая взятая наугад из пачки накладная оказалась неправильно оформленной, то пачка окажется неудовлетворительной; 2) вероятность того, что если две взятые наугад накладные оформлены неправильно, то пачка неудовлетворительна. Определим следующие события. С1 – пачка удовлетворительна, С2 – пачка неудовлетворительна (Р(С1) = 0,9; Р(С2) = 0,1); А – первая накладная оформлена неправильно, (Р(А/С1) = 0,01; Р(А/С2) = 0,05); В - обе накладные оформлены неправильно. Будем считать, что в пачке находится достаточно большое число накладных, чтобы считать, что вероятность появления второй неправильной накладной существенно не изменится и будет равна по прежнему 0,01 в удовлетворительной и 0,05 в неудовлетворительной пачке. На том же основании будем считать, что события А и появление второй неправильной накладной (обе накладные достаются из одной и той же пачки, В – произведение этих событий) независимы: Р(В/С1) = 0,0001; Р(В/С2) = 0,0025). Отметим, что события С1 и С2 несовместны. Событие С1 + С2 является достоверным. Нам необходимо определить Р(С2/А) и Р(С2/В). Для этого воспользуемся формулой Байеса: Р(С2/А) = Р(С2)*Р(А/С2)/( Р(С1)*Р(А/С1) + Р(С2)*Р(А/С2)) = 0,1*0,05 / (0,9*0,01 + 0,1*0,05) = 0,005/0,014 = 5/14  0,357 0,357Р(С2/В) = Р(С2)*Р(В/С2)/(Р(С1)*Р(В/С1) + Р(С2)*Р(В/С2)) = 0,1*0,0025 / (0,9*0,0001 + 0,1*0,0025) = 0,00025/0,00034 = 25/34  0,735. 0,735. |
