Теория вероятностей и математическая статистика. Закон распределения случайной величины. Математическое ожидание 28 Дисперсия случайной величины 32

• Название: Закон распределения случайной величины. Математическое ожидание 28 Дисперсия случайной величины 32
• Анкор: Теория вероятностей и математическая статистика.docx
• Дата: 01.12.2017
• Размер: 361.49 Kb.
• Имя файла: Теория вероятностей и математическая статистика.docx
• Тип: Закон; #10596
• страница: 3 из 12

Условная вероятность. Независимость событий

Рассмотрим следующий опыт. В урне находится четыре одинаковых на ощупь шара – 2 черных и 2 белых. Из урны дважды наугад (не глядя) вытаскивают по одному шару. Событие А – в первый раз вытащен белый шар, событие В – во второй раз вытащен белый шар.

Предположим вначале, что после того, как шар вытащен, и его цвет определен, его возвращают обратно в урну. Тогда можно рассматривать оба вытаскивания, как отдельные опыты, и оба раза вероятность каждого элементарного события (вытащен 1 из 4 шаров) будет равна ¼. Следовательно, так как белых шаров 2 в том и другом случае, Р(А) = Р(В) = 2/4 = 1/2.

Изменим условия опыта. Пусть теперь вытащенный шар не кладут обратно в урну. Тогда по-прежнему Р(А) = 1/2. Обозначим вероятность В при условии, что А произошло, Р(В/А). Если в первый раз вытащен белый шар, то в урне осталось 2 черных и 1 белый шар, т.е. могут иметь место три равновероятных исхода, из которых только 1 соответствует событию В. Р(В/А) = 1/3. Определим вероятность В при условии, что произошло 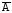, т.е. вытащен черный шар (т.е. не белый, шаров других цветов, кроме белого и черного, в урне нет). Тогда в урне осталось 2 белых и 1 черный шар, Р(В/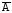) = 2/3.
Величины Р(В/А) и Р(В/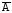) называют условными вероятностями. Строгое определение условной вероятности формулируется следующим образом:

Условной вероятностью называют вероятность события В, при условии, что событие А произошло, Р(В/А) = Р(АВ)/Р(А), где Р(А)>0.
Проиллюстрируем это определение на примере с шарами, в котором их возвращают в урну. Пронумеруем шары 1, 2, 3 и 4 (первые 2 – черные, а 3 и 4 – белые). Рассмотрим пространство элементарных событий (событие 12 означает, что в первый раз вытащили первый шар, а во второй – второй): {12; 13; 14; 21; 23; 24; 31; 32; 34; 41; 42; 43}. Возможны 12 равновероятных исходов. Событию АВ (и в первый, и во второй раз вытащены белые шары) соответствуют два из них - {34; 43}, значит, Р(АВ) = 2/12 = 1/6. Событию А соответствуют 6 исходов: {31; 32; 34; 41; 42; 43}, Р(А) = 1/2. Отсюда Р(В/А) = Р(АВ)/Р(А) = (1/6)/(1/2) = 1/3, что совпадает с ранее полученным результатом.
События А и В называют независимыми, если Р(В/А) = Р(В), Р(А)>0 (т.е. вероятность события В не зависит от того, произошло или нет событие А). В противном случае события являются зависимыми.

Другое определение независимости, эквивалентное данному (эквивалентность становится очевидной, если сравнить его с определением условной вероятности):

События А и В называют независимыми, если Р(АВ) = Р(В)*Р(А), Р(А)>0.
Например, в первом опыте с шарами, когда они возвращались в урну, события А и В были независимыми, а при изменении условий опыта (шары не возвращаются) они стали зависимыми.
Второе определение можно также рассматривать, как правило умножения независимых событий.
События А_i, i = 1,n называют взаимно независимыми (независимыми в совокупности), есл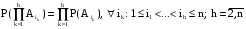и

(т.е. для любого набора событий из данной совокупности вероятность их произведения равна произведению вероятностей событий).

Если это условие выполняется для любых двух событий (т.е. только для h = 2, то события называют попарно независимыми.

Отметим, что из попарной независимости не следует взаимная независимость.
Очевидно, для взаимно независимых событий правило умножения можно обобщить на сколь угодно большое число событий: .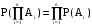
Правило умножения зависимых событий непосредственно следует из определения условной вероятности:

Р(АВ) = Р(А)*Р(В/А).

Методом индукции из него получают более общую формулу: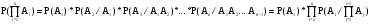

Например, на станции отправления имеется 8 заказов на отправку товара – 5 внутри страны и 3 на экспорт. Определим вероятность того, что два выбранных наугад заказа окажутся предназначенными для потребления внутри страны.

Данное событие представляет собой произведение двух зависимых событий: А – первый заказ на отправку внутри страны, В – второй заказ на отправку внутри страны. Р(А) = 5/8; Р(В/А) = 4/7 (так как если один заказ внутри страны уже выбрали, их осталось 4 из 7).

Р(АВ) = Р(А)*Р(В/А) = (5/8)*(4/7) = 20/56 = 5/16.
Другой пример: совет директоров состоит из трех бухгалтеров, трех менеджеров и двух инженеров. Из трех его членов планируется создать подкомитет (их выбор определяется соображениями, не связанными со специальностью). Определим вероятность того, что подкомитет будет полностью состоять из бухгалтеров.

Данное событие представляет собой произведение трех зависимых событий: А – 1-й член подкомитета – бухгалтер, В – 2-й – бухгалтер и С - 3-й - бухгалтер. Р(А) = 3/8; Р(В/А) = 2/7; Р(С/АВ) = 1/6. Отсюда Р(АВС) = Р(А)*Р(В/А)*Р(С/АВ) = (3*2*1)/(8*7*6) = 1/56.
Пример расчета вероятности произведения независимых событий: станок функционирует только при условии одновременной работы 3 независимых друг от друга узлов. Вероятность поломки этих узлов равна соответственно 0,2, 0,3 и 0,1. Определим вероятность бесперебойной работы станка в течении рассматриваемого периода (для которого определены вероятности).

Станок будет работать, если ни один из трех узлов не сломается.

Обозначим А событие “узел 1 не сломался”, В - “узел 2 не сломался”, С - “узел 3 не сломался”. Необходимо найти Р(АВС).

Событие, состоящее в том, что узел не сломался, является противоположным событию “узел сломался”. Значит, вероятность отсутствия поломки для каждого из трех станков можно подсчитать как 1-0,2 = 0,8; 1-0,3 = 0,7 и 1-0,1 = 0,9. Известно, что узлы работают независимо. Следовательно, Р(АВС) = Р(А)*Р(В)*Р(С) = 0,504.