Законы сложения и приведения переменных сил те же, что и для постоянных сил
 Скачать 1.63 Mb. Скачать 1.63 Mb.
|
|
Вывод. Центр масс является не материальной точкой, а геометрически он может не совпадать ни с одной из материальных точек системы (кольцо). Центр масс характеризует распределение масс в системе. Из формул (4.3), (4.2) видно, что положение центра масс системы зависит только от положения и массы каждой точки этой системы. Центр тяжести тел является центром масс этой системы. (Статика) Понятие «центр масс» применимо для любой системы материальной точки, тогда как понятие «центр тяжести» применяется лишь для механических систем, находящихся в однородном поле силы тяжести. Твердое тело. Рассмотрим систему точек, расстояние между которыми не меняется. Такая система называется неизменяемой.       Для образования неизменной системы каждую точку нужно соединить идеальными стержнями по крайней мере с тремя точками, уже входящими в неизменную систему. Считая число точек неизменяемой системы бесконечно большим, а длины соединяющих их идеальных стержней бесконечно малыми, получаем модель абсолютно твердого тела. Теорема о движении центра масс. ( Уравнения движения этих точек Суммируем эти уравнения. Преобразуем левую часть равенства т  .к. .к. Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил или главному вектору этих сил. Уравнение выражает теорему о движении центра масс системы, которая формируется следующим образом: центр масс механической системы движется как материальная точка массой, равной массе всей системы, к которой приложены все внешние силы, действующие на систему. П  роектируя (4.5) на координатные оси роектируя (4.5) на координатные осиСледствия из теоремы 1. Если 2. Если Пусть Дифференциальные уравнения поступательного движения твердого тела. При поступательном движении все точки тела движутся как его центр масс. Поэтому дифференциальные уравнения движения центра масс механической системы являются дифференциальными уравнениями поступательного движения твердого тела.  m – масса тела (С помощью этих уравнений решаются 2 задачи динамики). Таким образом, изучение поступательного движения твердого тела сводится к изучению движения отдельной материальной точки, имеющей массу всего тела. Импульс силы. Для характеристики действия, оказываемого на тело силой за некоторый промежуток времени вводится понятие об импульсе силы. Элементарным импульсом силы называется векторная величина Импульс силы 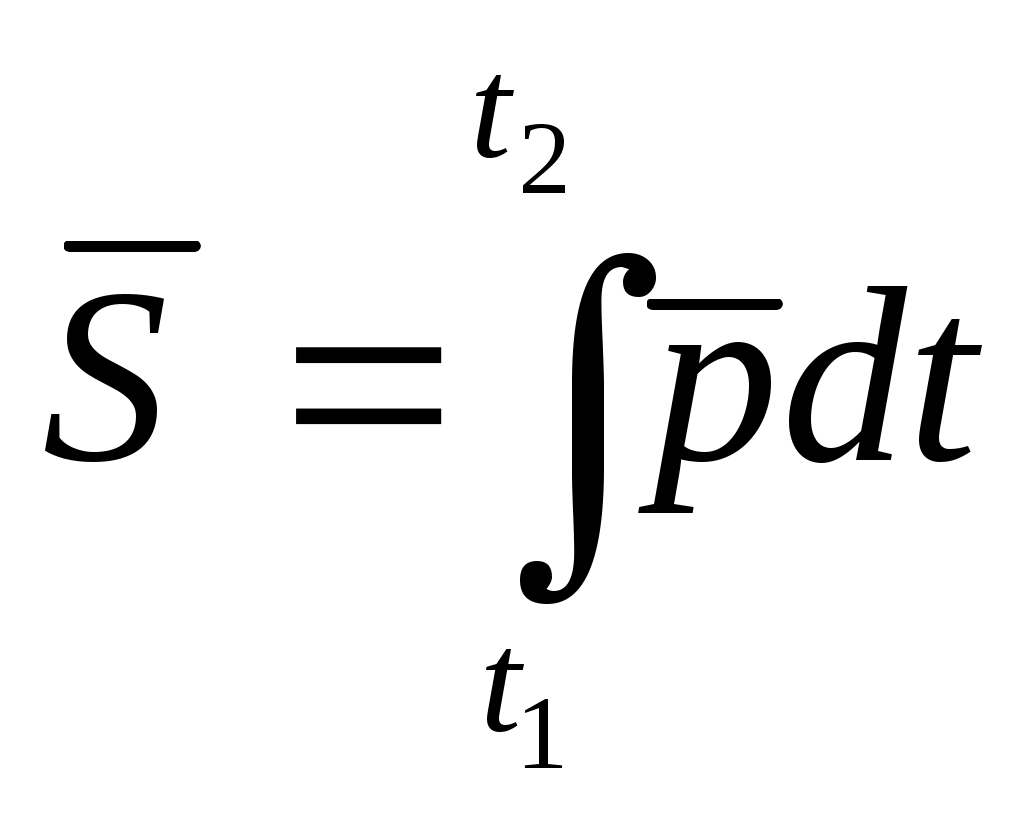 Импульс силы характеризует передачу точки механического движения со стороны, действующих на нее тел за данный промежуток времени. Если Н  айдем проекции айдем проекции 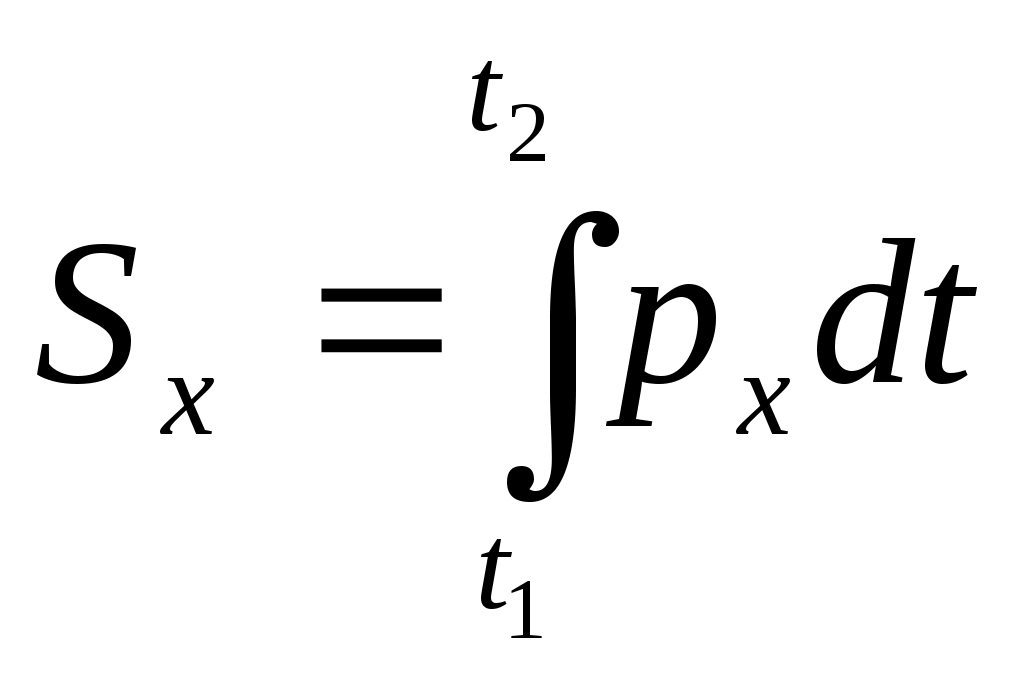 По этим проекциям можно найти сам вектор По этим проекциям можно найти сам вектор 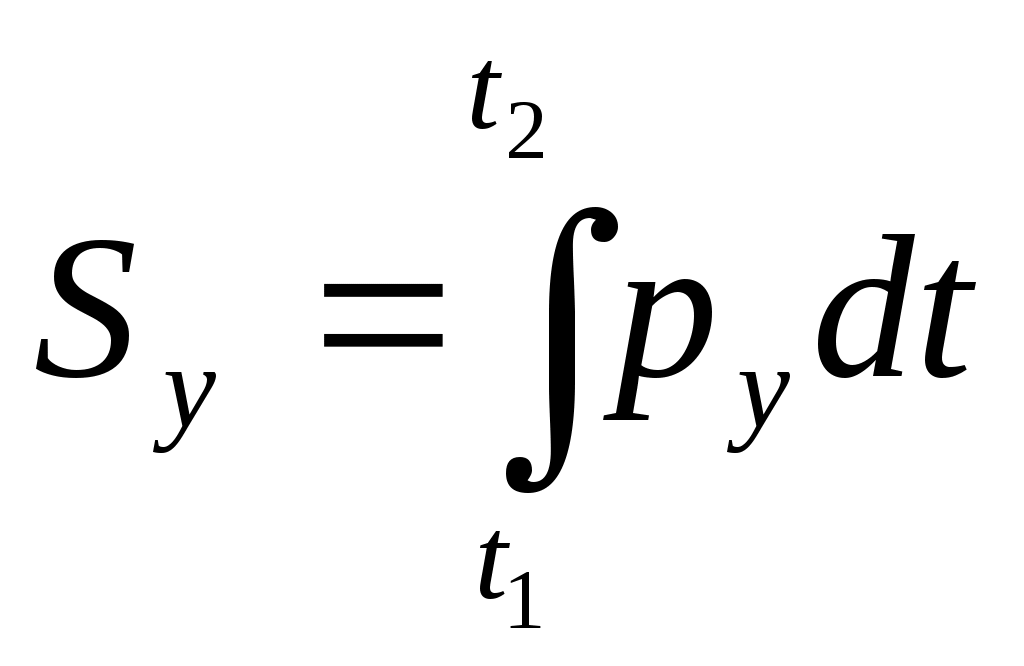 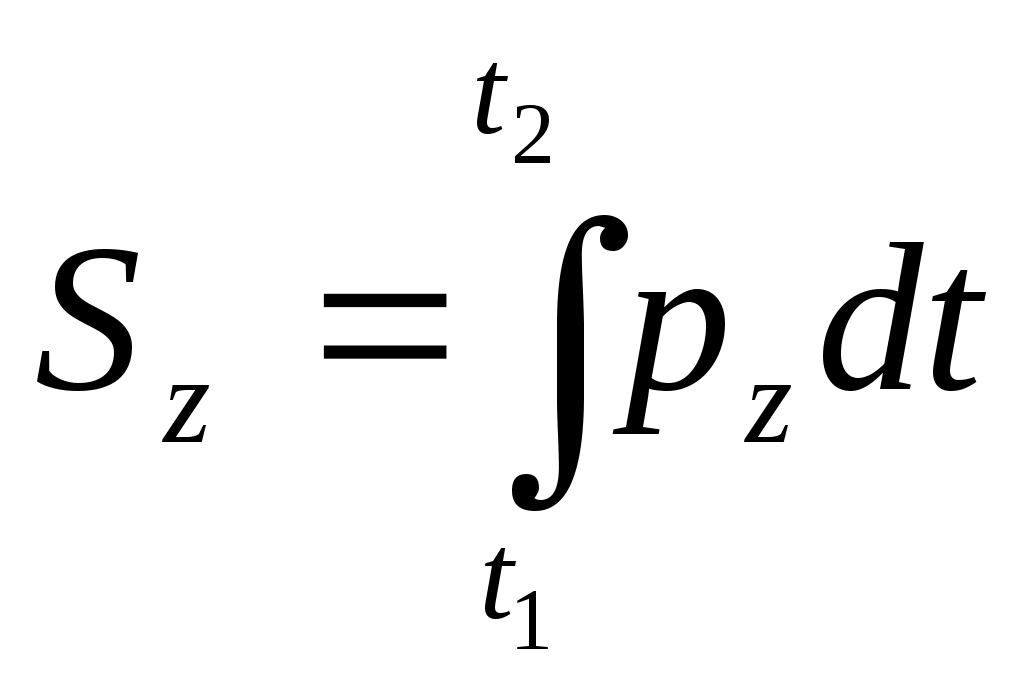 Импульс равнодействующей нескольких сил за некоторый промежуток времени равен геометрической сумме импульсов составляющих сил за тот же промежуток времени. Теорема об изменении количества движения материальной точки. Количеством движения материальной точки называется вектор, имеющий направление скорости и модуль, равный произведению массы точки на модуль скорости ее движения. Количество движения точки зависит от ее массы и скорости, является мерой механического движения. Р – равнодействующая, приложенных к точке сил. Основное уравнение динамики преобразуем следующим образом. Уравнение (5.8) выражает теорему об изменении Производная по времени от количества движения точки геометрически равна равнодействующей приложенных к точке сил. Запишем уравнение (5.8) в виде 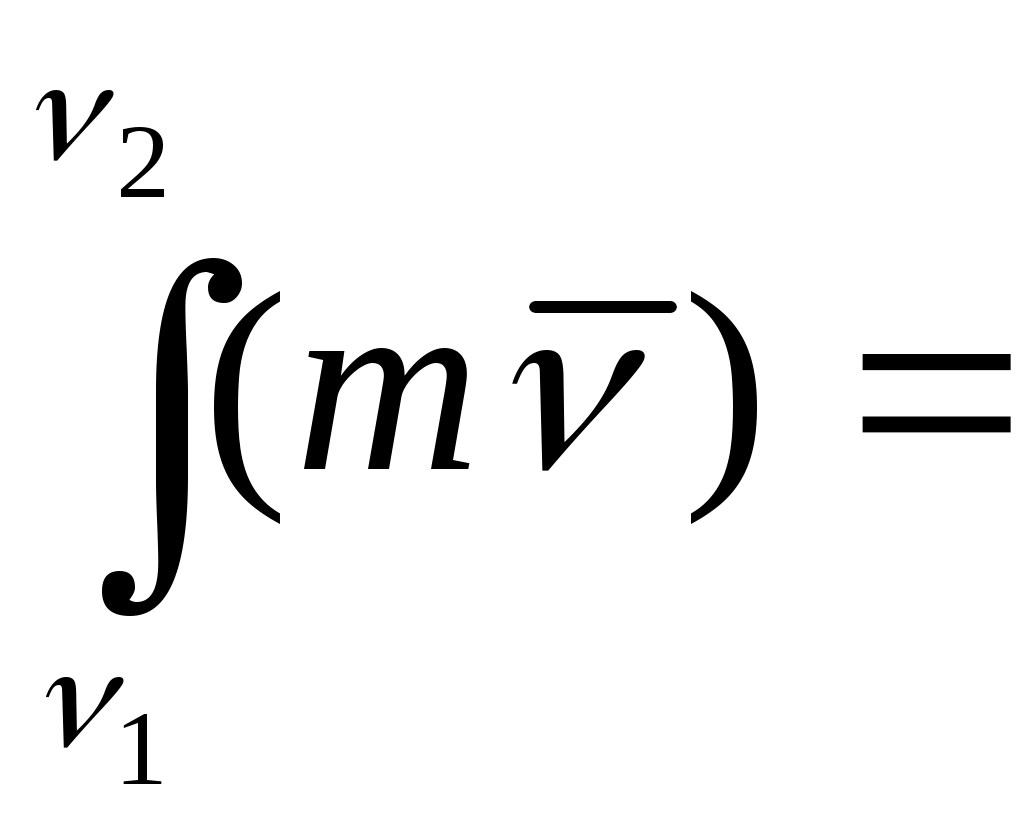 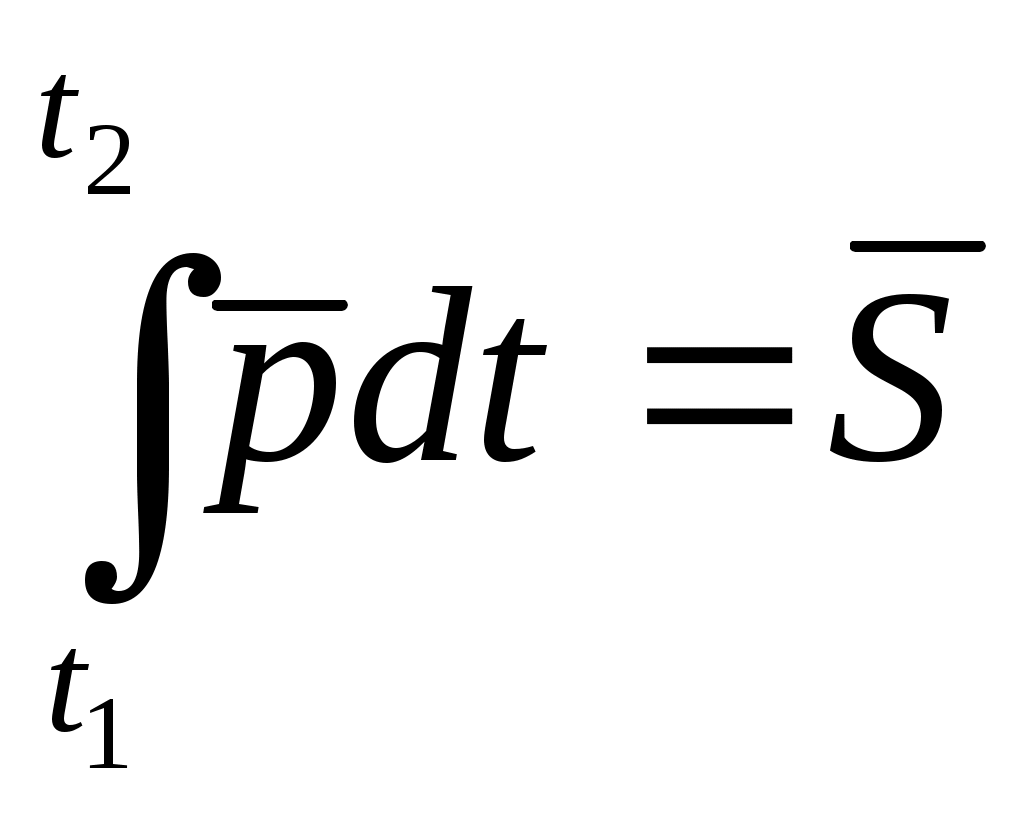 , получим , получимЗаменим в уравнении (5.9) импульс равнодействующими импульсами составляющих сил. Уравнение (5.10) выражает теорему об изменении количества движения материальной точки в конечной форме: И  зменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов сил, приложенных к точке за тот же промежуток времени (теорема импульсов). зменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов сил, приложенных к точке за тот же промежуток времени (теорема импульсов).Изменение проекции количества движения точки на данную ось за некоторый промежуток времени равно сумме проекции на ту же ось импульсов, приложенных к точке сил, за то же промежуток времени. Количество движения механической системы. Количеством движения механической системы называется вектор, равный геометрической сумме (главному вектору) количественного движения всех материальных точек этой системы Преобразуем это выражение. Вектор количества движения механической системы равный произведению массы системы на скорость ее центра масс, имеет направление скорости: Проектируем (6.2) на координатные оси.  (6.3) Продифференцируем (6.2) по времени (6.4) Производная по времени от Уравнению (6.4) соответствуют 3 уравнения в проекциях на оси координат (6.5) Из уравнений (6.4) и (6.5) следует, что изменение Следствия из теоремы: 1) Если за рассматриваемый промежуток времени, то количество движения механической системы const. 2) Если Найдем связь между изменение К и импульсами действующих на эту систему счисления. Для каждой точки м. с можно определить изменение количества движения за промежуток Суммируем правые и левые части уравнений. Получаем: И  зменение зменение |
