Законы сложения и приведения переменных сил те же, что и для постоянных сил
 Скачать 1.63 Mb.
|
  5) Шар массы М радиуса R  (9.14)Моменты инерции тела относительно параллельных осей. Теорема Гюйгенса. т. С оси  т. О оси Oxyz Oy // Cy’ Oz // Cz’ cCz’ и Oz=d По формулам (9.3)   Из рисунка видно, что для любой точки тела         =0т.к.   (9.15)Теорема Гюйгенса Момент инерции тела относительно данной оси равен моменту инерции относительно оси ей параллельной, проходящей через центр масс тела, сложенному с произведением массы всего тела на квадрат расстояния между осями. Из формулы (9.15) видно, что наименьший момент инерции будет у тела относительно оси, проходящей через точку С. Центробежные моменты инерции. Главные оси инерции. Дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси.     где   Таким образом, момент вращающегося твердого тела относительно неподвижной оси его вращения равен произведению момента инерции тела относительно той же оси на угловую скорость тела. Рассмотрим изменение кинетического момента твердого тела.     Уравнение справедливо и для движения системы вокруг центра масс.Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси. Сравним (10.2) с уравнением при вращательном движении является характеристикой инертности тела. Если  , то  , тело вращается ускоренно. , то  , вращение тела равномерное. , то  , вращение замедленное.Теорема о зависимости между кинетическими моментами механической системы относительно неподвижного центра и относительно центра масс. рис. Производная по времени от кинетического момента механической системы относительно центра масс системы в ее относительном движении по отношению к этому центру геометрически равна главному моменту внешних сил, действующих на точки системы относительно центра масс. Следствие: Если  , то  , и  .Д  ифференциальные уравнения плоского движения.      По теореме о движении центра масс 3 уравнение из (10.8)  т.к. относительное движение вращение  кинетический момент системы относительно оси получаем  Т  аким образом, дифференциальные уравнения имеют вид: « » - дзета « » - эта  « » - ксиУравнения плоского движения получим используя теоремы о движении центра масс и применении кинетического момента системы относительно центра масс для относительного движения системы по отношению к центру масс. С помощью этих уравнений можно решать 2 основные задачи динамики. Работа силы Для характеристики действия оказываемого силой на тело; при некотором его перемещении, вводится понятие о работе силы. Введем понятие элементарной механической работы силы  Элементарной работой силы называется скалярная величина (11.1).  ,где:  - проекция силы на касательную к траекторииds – элементарное бесконечно малое перемещение. (  , а не dA, т.к. в общем случае она не является дифференциалом функции).Элементарная работа является полным дифференциалом координат точки только для потенциальных сил. рис На изменение модуля скорости будет влиять только  силы составляющая  изменяет направление вектора скорости (сообщает точке нормальное ускорение). На модуль скорости не влияет. получим 2. Элементарная работа силы равна проекции силы на направление перемещения точки, умноженной на элементарное перемещение ds. 3. Элементарная работа силы равна произведению модуля силы на элементарное перемещение ds и на косинус угла между направлением силы и направлением перемещения.  , то работа «+» , то работа «-» , то и работа равна 0Работа всегда равна нулю.Из кинематики известно,     , тогда 4. Элементарная работа силы равна скалярному произведению вектора силы на вектор элементарного перемещения точки ее приложения. Найдем аналитической выражение элементарной работы. Силу разложим на составляющие ( ). Элементарное перемещение ds слагается из dx, dy, dz  Подставив и  в формулу - аналитическое выражение элементарной работыПолная работа силы Работа силы на конечном перемещении 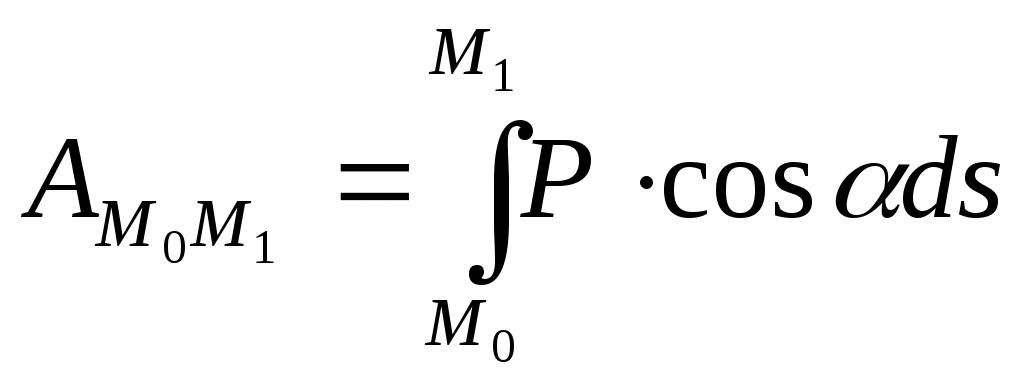 переходя к пределу этой суммы при бесконечно малых ds. (11.5) 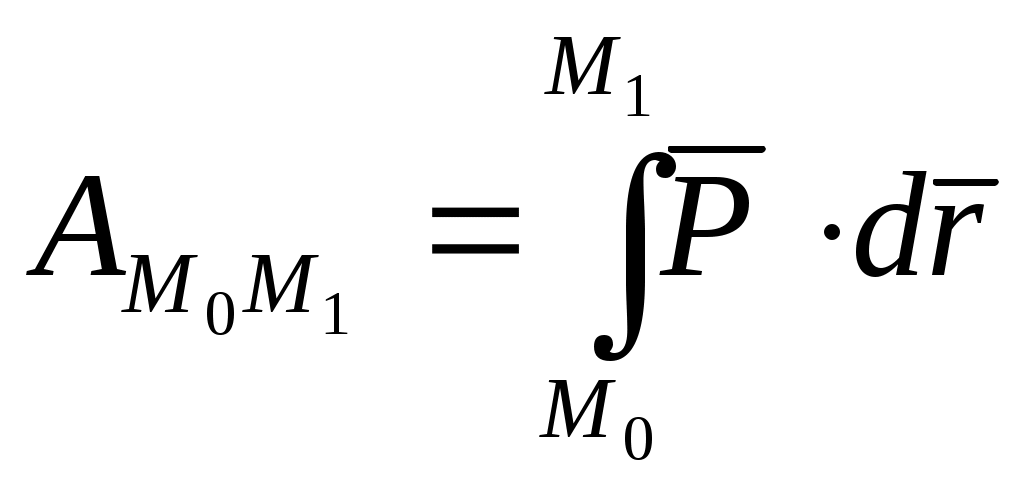 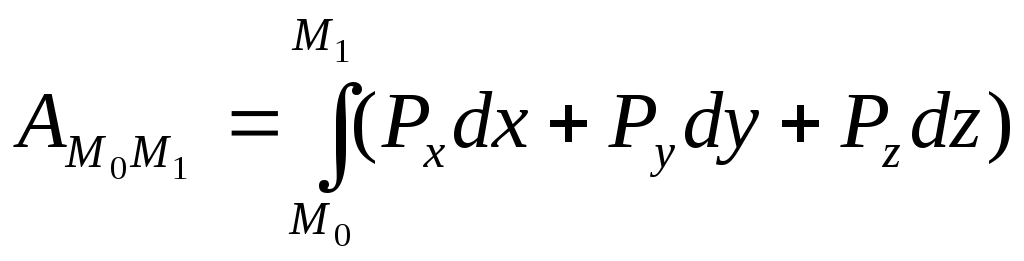 Работа силы на конечном перемещении  равна взятому вдоль этого перемещения интегралу от элементарной работы.Если сила const, то  , где    Теорема о работе силы. 1. Теорема. Работа равнодействующей силы на некотором перемещении равна алгебраической сумме работ составляющих сил на том же перемещении. на точку М действует система сил   точка получает элементарное перемещение 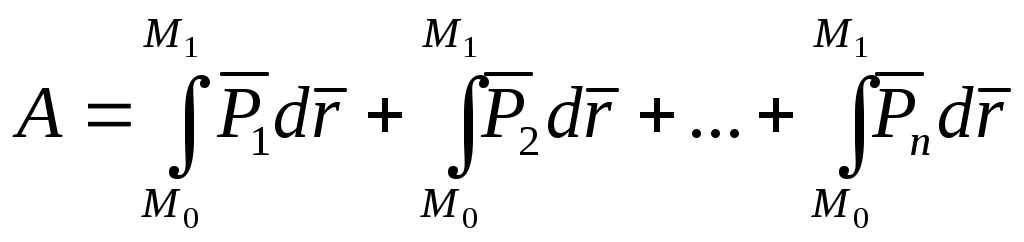   2. Теорема: Работа постоянной по модулю и направлению силы на результирующем перемещении равна алгебраической сумме работ этой силы на составляющих перемещениях. Точка получила совокупность последовательных перемещений  .Результирующее перемещение  Работа постоянной силы   Определяем интеграл по полному промежутку интегрирования равен сумме интегралов по составляющим.Мощность силы. Изменение работы силы к единице времени, называется мощностью силы. (N)   , то таким образом, мощность силы равна скалярному произведению векторов силы и скорости точки ее приложения. Аналитическое выражение мощности.  За единицу мощности в «СИ» 1 ватт = 1  «Лошадиная сила» 1 л.с. = 736 вт. Примеры вычисления работ. 1. Работа силы тяжести.  ,   подставляя это в формулу (11.5) 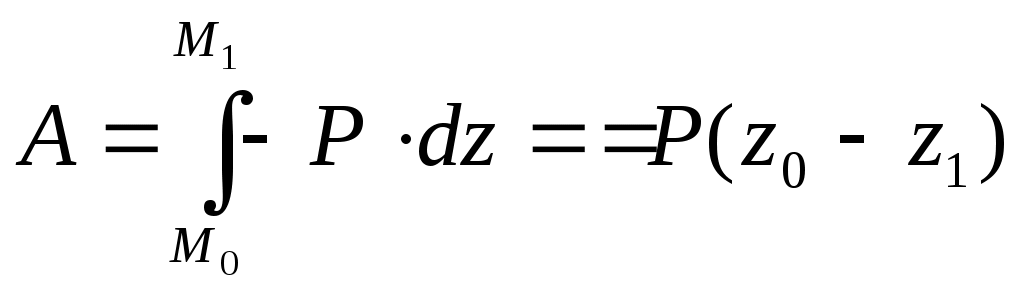  Работа силы тяжести равна взятому со знаком «+» или «-» произведению модуля силы на вертикальное перемещение точки ее приложения. Работа упругой силы. |