Законы сложения и приведения переменных сил те же, что и для постоянных сил
 Скачать 1.63 Mb.
|
 (6.7) Изменение проекции количества движения механической системы на любую ось равно сумме проекции импульсов всех внешних сил, действующих на систему, на ту же ось. Момент количества движения материальной точки относительно центра и относительно оси. Вычисляется момент вектора  так же, как и момент силы.  .  , если можно видеть, смотря навстречу оси, , вращающий против хода часовой стрелки. , если можно видеть, смотря навстречу оси, , вращающий по часовой стрелки. Проекция момента о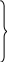тносительно центра на ось, проходящую через эту точку, равна моменту количества движения точки относительно этой оси.А  налитической выражение моментов количества движения точки относительно координатных осей имеют вид.   x, y, z - координаты точек  - проекции скорости точек на координатные оси.Теорема об изменении момента количества движения материальной точки.  Установим зависимость между 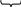 и  , для этого найдем      ||  0, т.к. угол между 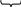и =0    Соотношение выражает теорему об изменении .Производная по времени от момента количества движения точки относительно некоторого центра равна геометрической сумме моментов сил, действующих на точку относительно того же центра. Проектируя (7.6) на оси x, y, z, получим Производная по времени от момента количества движения точки относительно некоторой неподвижной оси равна алгебраической сумме моментов сил, действующих на точку, относительно этой же оси. 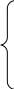    Следствия из теоремы. 1. Если линия действия равнодействующей приложенных к точке сил, все время проходит через некоторый неподвижный центр, то момент количества движения точки относительно данного ц3ентра остается постоянным. Из (7.6) следует, что если  , то  и  Примером этого следствия служит движение точки под действием центральных сил. Центральной силой называется сила, линия действия которой за время движения проходит через некоторый центр, а модуль зависит от расстояния между этим центром и точкой приложения силы.  и  .Из этого следует, что плоскость, проходящая точку с не изменяет своего положения. Т.е. траектория точки лежит в этой плоскости.2. Если момент равнодействующей приложенных к точке сил относительно некоторой оси все время равняется 0, то  остается ConstИз уравнения (7.7)   если  Понятие о секторной скорости. Закон площадей. рисунок Мы выяснили, что если , траектория точки лежит в плоскости ( и 0) и  - const (или  ).Момент (  ) относительно центра с всегда const.Этот результат имеет наглядное истолкование    , где  - площадь элемента  . Величина  определяет скорость, с которой растет площадь, ометаемая радиусом-вектором  при движении точки М и называется секторной скоростью точки.В нашем случае  .Таким образом, при движении под действием центральной силы точка движется по плоской кривой с постоянной секторной скоростью, т.е. так, что радиус-вектор точки в любые равные промежутки времени ометает равные площади (закон площадей). Этот закон имеет место при движении планет и выражает собой один из законов Кеплера.   А – афелий П – перигелий Кинетический момент механической системы относительно центра и оси. Кинетическим моментом, или главным моментом количеств движения механической системы относительно данного центра, называется вектор, равный геометрической сумме моментов количеств движения всех точек системы относительно этого центра.  Кинетический момент системы  Кинетическим моментом, или главным моментом количеств движения механической системы относительно оси, называется алгебраическая сумма моментов количеств движения всех точек системы относительно этой оси.  , то  Проекция кинетического момента механической системы относительно некоторого центра О на ось, проходящую через этот центр О, равна кинетическому моменту механической системы относительно этой оси. Моменты инерции твердого тела, радиус инерции. Движение системы, кроме действующих сил, зависит также от ее суммарной массы и распределения масс. (сумма масса, центр масс). Положение центра масс однако не полностью характеризует распределение масс системы. Например: При одновременном изменении h центр масс не меняется, а распределение масс станет другим, и это скажется на движении системы (вращение будет происходить медленнее). Поэтому в механике вводится еще одна характеристика распределения масс – момент инерции. Момент инерции твердого тела относительно оси вращения при вращательном движении является мерой его инертности. Моментом инерции тела (системы) относительно оси (или осевым моментом) называется скалярная величина, равная сумме произведения масс всех точек тела на квадраты их расстояний от точки до оси.  (всегда >0 и  )Моментом инерции твердого тела (системы) относительно полюса (полярным моментом инерции) называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояния оси точки до этого полюса.  Для вычисления осевых и полярных моментов инерции можно расстояния выражать через координаты  этих точек. ,  ,   из приведенных формул получим Для одной точке, находящейся на расстоянии h от оси момент инерции можно вычислить  Часто в ходе расчетов пользуются понятием радиуса инерции. Радиусом инерции тела относительно оси OZ называется линейная величина  определяемая равенством ( - радиус инерции)Из определения следует, что радиус инерции геометрически равен расстоянию от оси OZ той точки, в которой надо сосредоточить массу всего тела, чтобы момент инерции этой точки был равен моменту инерции всего тела. Записанные формулы справедливы для механической системы и любого твердого тела. Для сплошного твердого тела, разбивая его на элементарные части, найдем, что в пределе сумма, стоящая в равенстве (9.1), обратится в интеграл    - элементарный объем - плотность и h зависят от координаты точки.Поэтому формулы (9.3) примут вид.  Если тело однородное, то   Найдем моменты инерции некоторых однородных тел. 1) Тонкий однородный стержень длины l, массы М. рисунки h = х 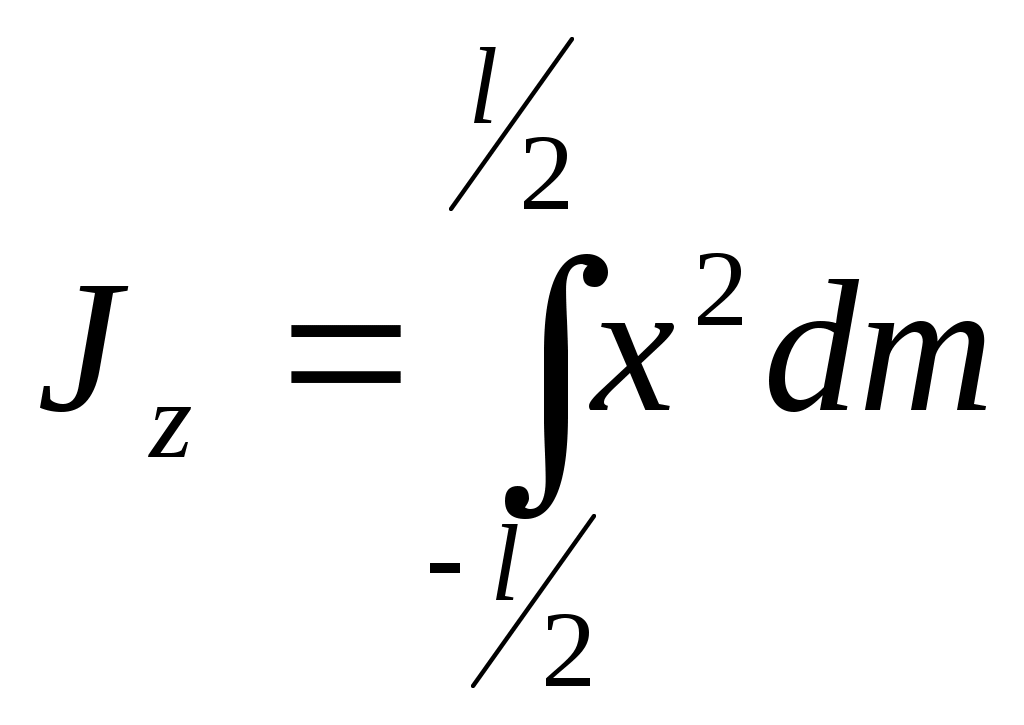      (9.10)2. Тонкое однородное кольцо радиуса R и массы М. т.к.  , то получим  (9.11)такой же результат для тонкой цилиндрической оболочки массы М и радиуса R относительно ее оси. 3. Круглая однородная пластинка или цилиндр радиуса R и массы М. Если выделим элементарное кольцо радиуса r и толщины dr Площадь его  масса  где  масса единичной площади dm  (9.12).4) Прямоугольная пластинка массы М со сторонами а, b |