МС, Тр, ХТОВ. Занятие 1

• Название: Занятие 1
• Дата: 17.11.2022
• Размер: 0.95 Mb.
• Имя файла: МС, Тр, ХТОВ.docx
• Тип: Занятие; #792975
• страница: 21 из 30

Решение.

1. 
   Введём обозначение A=a+b. Тогда Y ^{3 Ac}.
   

f

2. 
   Прологарифмируем левую и правую части заданной зависимости
   

ln Y ln 3  ln A ln c ln f.

3. 
   Найдём дифференциал правой и левой частей
   

dln Y dln 3  dln A dln c dln f.

С учётом того, что dln 3  0, получим

dln Y dln A dln c dln f.

4. 
   Учитывая, что дифференциал от логарифма переменной величины
   

находится по формуле dln x  ^{dln x}dx ^dx

dx x

dY_ dA_ dc_ df_.

Y A c f

5. 
   Произведём широко используемую в теории погрешностей замену дифференциалов малыми абсолютными погрешностями (при условии, что
   

абсолютные погрешности достаточно малы), т.е.

dY Y, dA A,

dc c,

df f
Y_ A_ c_ f_.

Y A c f

6. 
   Учитывая, что знаки погрешностей
   

A, c, f

заранее неизвест-

ны, для получения гарантированной (предельной) оценки относительной погрешности косвенного измерения Y в последней формуле все знаки «–» заменяем на знаки «+». Таким образом, получили предельную оценку от- носительной погрешности косвенного измерения

  Y  A  c  f

     .

 Y _пр A c f

Здесь A=a+b, тогда A a b. Окончательно

  Y  a b  c  f

  

 Y _пр

a b

  .

c f

7. 
   Предельную оценку абсолютной погрешности косвенного измере- ния находим по формуле Y_пр  Y_прY, т.е.
   


^  a b

Y_пр  

 c_


 f^ 3a bc





.


^ a b

c f _ f

8. 
   Найдём среднеквадратические оценки относительной и абсолют- ной погрешностей косвенного измерения Yс учётом того, что
   

A_ск 

:
Y_ск  ;

Y_ск 



3abc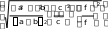

.

f

