Заочное отделение
 Скачать 0.86 Mb. Скачать 0.86 Mb.
|
|
Матричный метод: Обозначим через А — матрицу коэффициентов при неизвестных; X — матрицу-столбец неизвестных; B - матрицу-столбец свободных членов: Вектор B: BT=(4,2,0) С учетом этих обозначений данная система уравнений принимает следующую матричную форму: А*Х = B. Если матрица А — невырожденная (ее определитель отличен от нуля, то она имеет обратную матрицу А-1. Умножив обе части уравнения на А-1, получим: А-1*А*Х = А-1*B, А-1*А=Е. Это равенство называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А-1. Система будет иметь решение, если определитель матрицы A отличен от нуля. Найдем главный определитель. ∆=2•(2•5-(-1•13))-5•(-1•5-(-1•5))+3•(-1•13-2•5)=-23 Итак, определитель -23 ≠ 0, поэтому продолжаем решение. Для этого найдем обратную матрицу через алгебраические дополнения. Пусть имеем невырожденную матрицу А: = Тогда: = где Aij — алгебраическое дополнение элемента aij в определителе матрицы А, которое является произведением (—1)i+j на минор (определитель) n-1 порядка, полученный вычеркиванием i-й строки и j-го столбца в определителе матрицы А. Вычисляем алгебраические дополнения. ∆1,1=(2•5-(-1•13))=23 ∆1,2=-(5•5-3•13)=14 ∆1,3=(5•(-1)-3•2)=-11 ∆2,1=-(-1•5-(-1•5))=0 ∆2,2=(2•5-3•5)=-5 ∆2,3=-(2•(-1)-3•(-1))=-1 ∆3,1=(-1•13-2•5)=-23 ∆3,2=-(2•13-5•5)=-1 ∆3,3=(2•2-5•(-1))=9 Из полученных алгебраических дополнений составим присоединенную матрицу C: Вычислим обратную матрицу: Вектор результатов X X=A-1 • B XT=(-4,-2,2) x1=92 / (-23)=-4 x2=46 / (-23)=-2 x3=-46 / (-23)=2 Проверка. 2•(-4)-1•(-2)+5•2=4 5•(-4)+2•(-2)+13•2=2 3•(-4)-1•(-2)+5•2=0 Метод Крамера: Запишем систему в виде: BT = (4,2,0) Система совместна тогда и только тогда, когда системный (главный) определитель не равен нулю. Найдем определитель: Минор для (1,1): Вычеркиваем из матрицы 1-ю строку и 1-й столбец.
Получаем: Найдем определитель для этого минора. ∆1,1 = (2*5-(-1)*13) = 23 Минор для (2,1): Вычеркиваем из матрицы 2-ю строку и 1-й столбец.
Получаем: Найдем определитель для этого минора. ∆2,1 = ((-1)*5-(-1)*5) = 0 Минор для (3,1): Вычеркиваем из матрицы 3-ю строку и 1-й столбец.
Получаем: Найдем определитель для этого минора. ∆3,1 = ((-1)*13-2*5) = -23 Определитель: ∆ = (-1)1+12*23+(-1)2+15*0+(-1)3+13*(-23) = 2*23-5*0+3*(-23) = -23 Заменим 1-й столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы. Минор для (1,1): Вычеркиваем из матрицы 1-ю строку и 1-й столбец.
Получаем: Найдем определитель для этого минора. ∆1,1 = (2*5-(-1)*13) = 23 Минор для (2,1): Вычеркиваем из матрицы 2-ю строку и 1-й столбец.
Получаем: Найдем определитель для этого минора. ∆2,1 = ((-1)*5-(-1)*5) = 0 Минор для (3,1): Вычеркиваем из матрицы 3-ю строку и 1-й столбец.
Получаем: Найдем определитель для этого минора. ∆3,1 = ((-1)*13-2*5) = -23 Определитель минора: ∆1 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = (-1)1+14*23+(-1)2+12*0+(-1)3+10*(-23) = 4*23-2*0+0*(-23) = 92 Заменим 2-й столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы. Минор для (1,1): Вычеркиваем из матрицы 1-ю строку и 1-й столбец.
Получаем: Найдем определитель для этого минора. ∆1,1 = (2*5-0*13) = 10 Минор для (2,1): Вычеркиваем из матрицы 2-ю строку и 1-й столбец.
Получаем: Найдем определитель для этого минора. ∆2,1 = (4*5-0*5) = 20 Минор для (3,1): Вычеркиваем из матрицы 3-ю строку и 1-й столбец.
Получаем: Найдем определитель для этого минора. ∆3,1 = (4*13-2*5) = 42 Определитель минора: ∆2 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = (-1)1+12*10+(-1)2+15*20+(-1)3+13*42 = 2*10-5*20+3*42 = 46 Заменим 3-й столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы. Минор для (1,1): Вычеркиваем из матрицы 1-ю строку и 1-й столбец.
Получаем: Найдем определитель для этого минора. ∆1,1 = (2*0-(-1)*2) = 2 Минор для (2,1): Вычеркиваем из матрицы 2-ю строку и 1-й столбец.
Получаем: Найдем определитель для этого минора. ∆2,1 = ((-1)*0-(-1)*4) = 4 Минор для (3,1): Вычеркиваем из матрицы 3-ю строку и 1-й столбец.
Получаем: Найдем определитель для этого минора. ∆3,1 = ((-1)*2-2*4) = -10 Определитель минора: ∆3 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = (-1)1+12*2+(-1)2+15*4+(-1)3+13*(-10) = 2*2-5*4+3*(-10) = -46 Выпишем отдельно найденные переменные Х Проверка. 2*(-4)-1*(-2)+5*2 = 4 5*(-4)+2*(-2)+13*2 = 2 3*(-4)-1*(-2)+5*2 = 0 Методом Гаусса-Жордана найти решение системы уравнений Запишем систему в виде:
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы. Разрешающий элемент равен (2). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника. Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ. НЭ = СЭ - (А*В)/РЭ РЭ - разрешающий элемент (2), А и В - элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ. Представим расчет каждого элемента в виде таблицы:
В итоге получаем:
Разрешающий элемент равен (-1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
В итоге получаем:
Разрешающий элемент равен (3). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
В итоге получаем:
Ранг основной матрицы системы равен r(A)=3. Ранг расширенной матрицы равен r=4 (в основной матрице системы имеется нулевая строка). Таким образом, система не имеет решения. ГИТИС Заочное отделение ДКР№1. ВАРИАНТ№5 Предприятие выпускает изделия трех видов: А, В и С. В производстве каждого изделия используется сырье трех типов: S1, S2 и S3. Нормы расхода сырья на каждое изделие и ежедневный объем израсходованного сырья приведены в таблице.
Найти ежедневный объем выпуска изделий каждого вида Пусть ежедневно фабрика выпускает x1 шт. изделия S1, x2 шт. изделия S2 и x3 шт. изделия S3. Запишем это в виде столбца суточного выпуска продукции X. Далее выпишем матрицу технико-экономических коэффициентов A, а также столбец суточного расхода сырья В. 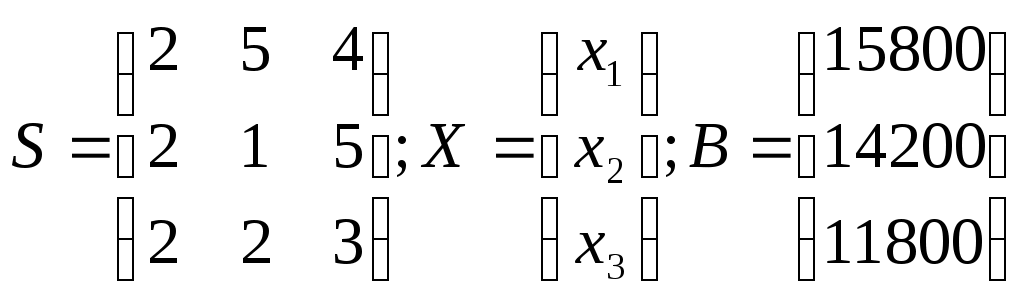 В результате получаем следующую систему уравнений для определения суточного выпуска продукции: 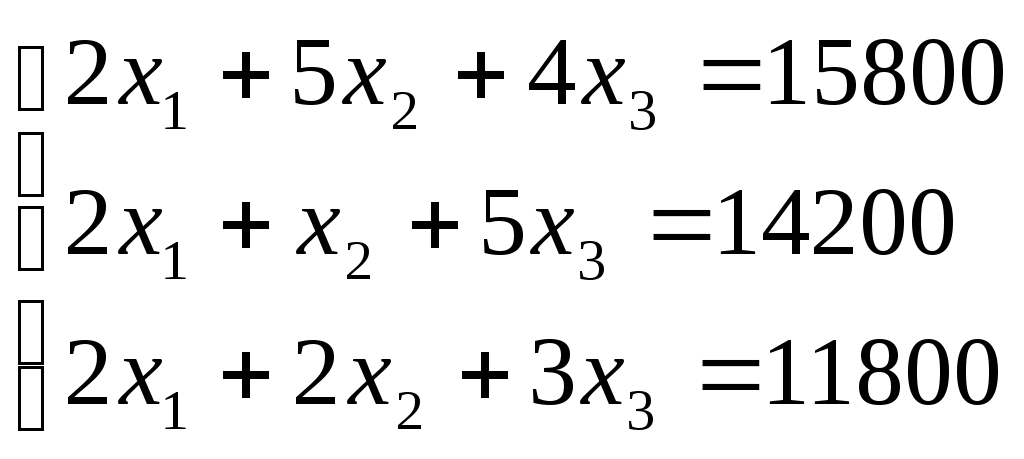 Работаем со столбцом №1 Умножим 2-ю строку на (k = -2 / 2 = -1) и добавим к 3-й:
Умножим 1-ю строку на (k = -2 / 2 = -1) и добавим к 2-й:
Работаем со столбцом №2 Умножим 2-ю строку на (k = 1 / 4 = 1/4) и добавим к 3-й:
Получим единицы на главной диагонали. Для этого всю строку делим на соответствующий элемент главной диагонали: Теперь исходную систему можно записать как: x1 = 7900 - (5/2x2 + 2x3) x2 = 400 - ( - 1/4x3) x3 = 1600 Из 3-ой строки выражаем x3 x3 = 1600 Из 2-ой строки выражаем x2 x2 = 400 - (-1/4)*1600 = 800 Из 1-ой строки выражаем x1 x1 = 7900 - 5/2*800 - 2*1600 = 2700 Найти произведение матриц АВ, если 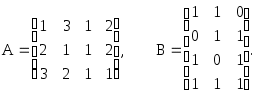 Вычисляем элемент новой матрицы (1,1): работаем с 1-ой строкой и с 1-м столбцом. Получаем: 1*1+3*0+1*1+2*1 = 4 Вычисляем элемент новой матрицы (1,2): работаем с 1-ой строкой и с 2-м столбцом. Получаем: 1*1+3*1+1*0+2*1 = 6 Вычисляем элемент новой матрицы (2,1): работаем с 2-ой строкой и с 1-м столбцом. Получаем: 2*1+1*0+1*1+2*1 = 5 Вычисляем элемент новой матрицы (2,2): работаем с 2-ой строкой и с 2-м столбцом. Получаем: 2*1+1*1+1*0+2*1 = 5 В итоге получаем матрицу AxB Матричным методом и по правилу Крамера найти решение системы уравнений 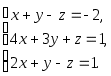 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
