Заочное отделение
 Скачать 0.86 Mb. Скачать 0.86 Mb.
|
|
Получаем: Найдем определитель для этого минора. ∆3,1 = (8*(-3)-(-1)*2) = -22 Определитель минора: ∆2 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = (-1)1+13*(-1)+(-1)2+12*8+(-1)3+11*(-22) = 3*(-1)-2*8+1*(-22) = -41 Заменим 3-й столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы. Минор для (1,1): Вычеркиваем из матрицы 1-ю строку и 1-й столбец.
Получаем: Найдем определитель для этого минора. ∆1,1 = (4*0-5*(-1)) = 5 Минор для (2,1): Вычеркиваем из матрицы 2-ю строку и 1-й столбец.
Получаем: Найдем определитель для этого минора. ∆2,1 = (4*0-5*8) = -40 Минор для (3,1): Вычеркиваем из матрицы 3-ю строку и 1-й столбец.
Получаем: Найдем определитель для этого минора. ∆3,1 = (4*(-1)-4*8) = -36 Определитель минора: ∆3 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = (-1)1+13*5+(-1)2+12*(-40)+(-1)3+11*(-36) = 3*5-2*(-40)+1*(-36) = 59 Выпишем отдельно найденные переменные Х Проверка. 3*2.98+4*(-0.837)+2*1.204 = 8 2*2.98+4*(-0.837)-3*1.204 = -1 1*2.98+5*(-0.837)+1*1.204 = 0 Методом Гаусса-Жордана найти решение системы уравнений Запишем систему в виде:
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы. Разрешающий элемент равен (1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника. Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ. НЭ = СЭ - (А*В)/РЭ РЭ - разрешающий элемент (1), А и В - элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ. Представим расчет каждого элемента в виде таблицы:
В итоге получаем:
Разрешающий элемент равен (-2). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
В итоге получаем:
Разрешающий элемент равен (-0.5). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
В итоге получаем:
Разрешающий элемент равен (-1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
В итоге получаем:
x1=1 x2=3 x3=1 x4=-1 Теперь исходную систему можно записать так (общее решение): x1 = 1 x2 = 3 - 2x5 x3 = 1 - x5 x4 = -1 + x5 Базисное решение получаем приравниванием переменной x5 к нулю. x1 = 1 x2 = 3 x3 = 1 x4 = -1 ГИТИС Заочное отделение ДКР№1. ВАРИАНТ№2 Предприятие выпускает изделия трех видов: А, В и С. В производстве каждого изделия используется сырье трех типов: S1, S2 и S3. Нормы расхода сырья на каждое изделие и ежедневный объем израсходованного сырья приведены в таблице.
Найти ежедневный объем выпуска изделий каждого вида Пусть ежедневно фабрика выпускает x1 шт. изделия S1, x2 шт. изделия S2 и x3 шт. изделия S3. Запишем это в виде столбца суточного выпуска продукции X. Далее выпишем матрицу технико-экономических коэффициентов A, а также столбец суточного расхода сырья В. 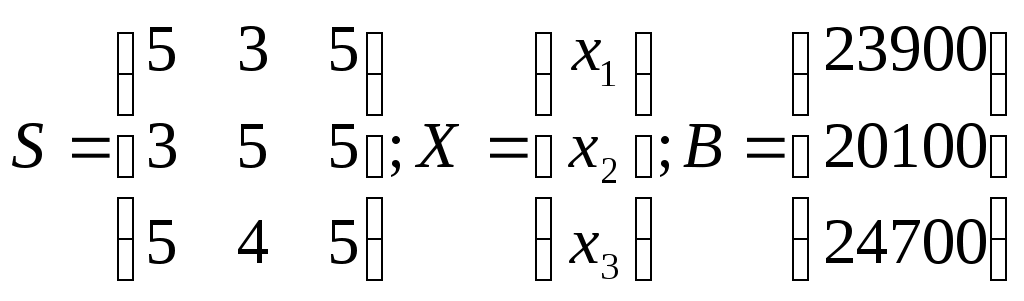 В результате получаем следующую систему уравнений для определения суточного выпуска продукции: 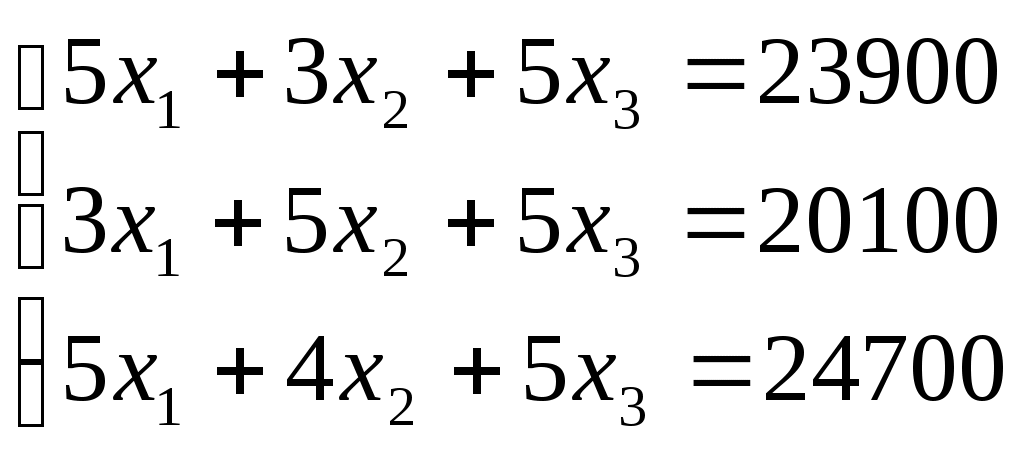 Для удобства вычислений поменяем строки местами: Работаем со столбцом №1 Умножим 2-ю строку на (k = -3 / 5 = -3/5) и добавим к 3-й:
Умножим 1-ю строку на (k = -5 / 5 = -1) и добавим к 2-й:
Работаем со столбцом №2 Умножим 2-ю строку на (k = -13/5 / 1 = -13/5) и добавим к 3-й:
Получим единицы на главной диагонали. Для этого всю строку делим на соответствующий элемент главной диагонали: Теперь исходную систему можно записать как: x1 = 4780 - (3/5x2 + x3) x2 = 800 x3 = 1600 Из 3-ой строки выражаем x3 x3 = 1600 Из 2-ой строки выражаем x2 x2 = 800 = 800 Из 1-ой строки выражаем x1 x1 = 4780 - 3/5*800 - 1*1600 = 2700 Найти произведение матриц АВ, если Вычисляем элемент новой матрицы (1,1): работаем с 1-ой строкой и с 1-м столбцом. Получаем: 1*3+2*1+1*3+1*1 = 9 Вычисляем элемент новой матрицы (1,2): работаем с 1-ой строкой и с 2-м столбцом. Получаем: 1*1+2*1+1*1+1*0 = 4 Вычисляем элемент новой матрицы (2,1): работаем с 2-ой строкой и с 1-м столбцом. Получаем: 2*3+1*1+1*3+1*1 = 11 Вычисляем элемент новой матрицы (2,2): работаем с 2-ой строкой и с 2-м столбцом. Получаем: 2*1+1*1+1*1+1*0 = 4 В итоге получаем матрицу AxB Матричным методом и по правилу Крамера найти решение системы уравнений | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
