реконструкция. Звена

Название	Звена
Анкор	реконструкция
Дата	16.11.2022
Размер	6.05 Mb.
Формат файла
Имя файла	bibliofond.ru_652307.rtf
Тип	Документы #792425
страница	7 из 11

1 2 3 4 5 6 7 8 9 10 11

где

- максимальный приведенный момент инерции, кг·м²;

- произвольно выбранный отрезок, мм.

Переведем все приведенные моменты инерции (

) в данный масштабный коэффициент и построим диаграмму.

Для построения диаграммы по оси абсцисс откладываем

, а по оси ординат

Для построения диаграммы для каждого положения откладываем соответствующие значения (

) и соединяем полученные точки плавной кривой.
.7 Построение диаграммы энергия-масса
Построение диаграммы происходит следующим образом: по оси

откладываем ординаты

из диаграммы изменения кинетической энергии, а по оси

- ординаты

диаграммы приведенных моментов инерции, соответствующие одному и тому же положению механизма. Номера положений фиксируем на пересечении соответствующих координат диаграммы. В итоге получим замкнутую кривую.

.8 Определение значения момента инерции маховой массы
По справочной таблице выберем коэффициент неравномерности хода ДВС:

Вычислим максимальный и минимальный угол наклона касательной:

Проведем касательные к диаграмме энергия-масса сверху и снизу под углами

до пересечения с осью

.

Замерим отрезок

, между точками пересечения касательных и осью изменения энергии, и определим приведенный момент инерции маховой массы:

.

. Простые зубчатые механизмы
.1 Структурный анализ простого зубчатого механизма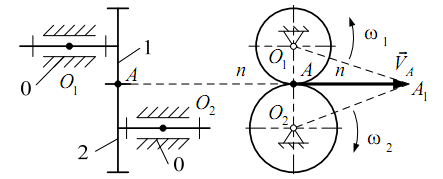

Рис.7.1 Схема простого зубчатого механизма с внешним зацеплением.
Структурный анализ простых зубчатых механизмов сводится к определению подвижности механизма.

Подвижность механизма определяем по формуле Чебышева:

(5.1)
где W - подвижность механизма;

n - число подвижных звеньев;

p₁ и p₂- соответственно число пар пятого и четвертого класса.
Таблица 5.1 - звенья простого зубчатого механизма

№ п.п	Номер звена	Вид совершаемого движения	Схема	Кинематическое состояние
1	1	Вращательное		Подвижное
2	2	Вращательное		Подвижное
3	0	_____		неподвижное

В структуру механизма входят два подвижных звена (зубчатые колеса) и стойка, представленная двумя шарнирно-неподвижными опорами. Следовательно, n=2.
Таблица5.2 - кинематические пары

Номер звена	Схема	Название	Класс/ подвижность	Вид контакта/замыкание
1-2		зубчатая	4/2	Линия (высшая)/ геометрическое
0-2		вращательная	5/1	По поверхности (низшая)/ геометрическое
0-1		вращательная	5/1	По поверхности (низшая)/ геометрическое

Кинематические пары 0-1 и 0-2 являются вращательными парами пятого класса, следовательно, p₁=2.

Кинематическая пара 1-2 является зубчатой парой четвертого класса, следовательно, p₂=1.

Подставим число подвижных звеньев и число пар пятого и четвертого классов в формулу Чебышева:

(5.2)

Полученный результат означает, что для однозначного описания положения всех звеньев механизма в рассматриваемой плоскости достаточно знать одну обобщенную координату.
.2 Синтез эвольвентного зацепления простого зубчатого механизма
Данная задача сводится к выполнению синтеза эвольвентных профилей зубчатых колес простой зубчатой передачи с внешним зацеплением.

Дано:

;

.

Найдем инволюту угла зацепления:

(5.3)

.
По таблице значений инвалют найдем угол зацепления:

Найдем минимальную величину коэффициента смещения для шестерни:

(5.4)

Величина коэффициента смещения для колеса определяется по блокирующему контуру.

Действительная величина коэффициента смещения для колеса: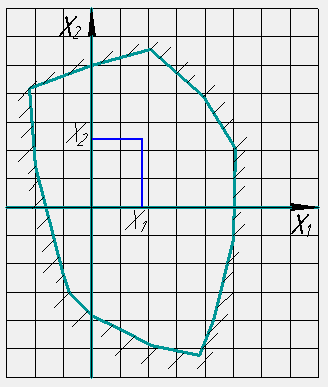

(5.5)

Рисунок 5.1 - блокирующий контур
Величину коэффициента смещения для колеса найдем по блокирующему контуру (рисунок 5.1): полученная точка попадает в границы контура, а это значит, что значения подобранны верно.
Далее будем находить диаметры делительных окружностей:

Для шестерни: