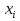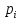ответы по терверу по 37. 1. Классификация случайных событий возможные и невозможные события, совместные и несовместные, противоположные и достоверные события. Примеры
 Скачать 4.53 Mb. Скачать 4.53 Mb.
|
   1. Классификация случайных событий: возможные и невозможные события, совместные и несовместные, противоположные и достоверные события. Примеры. 1. Классификация случайных событий: возможные и невозможные события, совместные и несовместные, противоположные и достоверные события. Примеры. Пространство элементарных событий Каждый из равновозможных результатов испытаний называется элементарным исходом или (элементарным событием). Всякий мыслимый результат эксперимента называют элементарным событием и обычно обозначают буквами Пространством элементарных событий называется множество всех взаимно исключающих исходов эксперимента такое, что результатом эксперимента всегда является один и только один исход. Пространство элементарных событий обычно обозначается и считается заданным, если указаны все его элементы. Из элементарных исходов можно составить более сложное событие. Результат испытания называется событием, независимо от его значимости. Результат испытания, который нельзя заранее прогнозировать, называется случайным событием. Любое подмножество данного множества интерпретируется как событие (возможно, и ненаблюдаемое). Совокупность всех наблюдаемых событий составляет множество событий для данного эксперимента. Множество для данного испытания может быть дискретным, или иметь более сложную структуру. К дискретным относятся конечные или счетные множества элементарных исходов. Построение множества (если оно не задано при описании эксперимента) осуществляется на практике, исходя из требования, чтобы все интересующие нас результаты данного эксперимента могли быть однозначно описаны на основе построенного множества . Другими словами, если нас интересуют события и т.д., являющиеся наблюдаемыми событиями в данном эксперименте, то множество должно состоять из таких исходов, чтобы существовали подмножества данного множества, равносильные событиям ит.д. Наступление события, благоприятствующие исходы Каждое случайное событие определяется как подмножество в множестве элементарных событий . При этом те элементарные события из , при которых событие наступает (т.е. принадлежит подмножеству ) называют благоприятствующими событию . Говорят, что событие произошло (наступило, осуществилось, реализовалось), если результатом эксперимента явился элементарный исход , принадлежащий (). Совместные (совместимые), несовместные (несовместимые) события Два события называются совместными (совместимыми) в данном опыте, если появление одного из них не исключает появления другого. Два события называются несовместными (несовместимыми) в данном опыте, если они не могут произойти вместе при одном и том же испытании. Несколько событий называются несовместными, если они попарно несовместны. Другими словами, события и совместны, если соответствующие множества и имеют общие элементы, и несовместны в противном случае, если появление одного из них исключает появление другого, и соответствующие множества и не имеют общих элементов, т.е. пересечение этих множеств является пустым множеством. Достоверное и невозможное события Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий . Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий . Событие, совпадающее с пустым множеством , называется невозможным событием, а событие, совпадающее со всем множеством , называется достоверным событием. События называют равновозможными, если нет основания полагать, что одно событие является более возможным, чем другие. Теория вероятностей есть наука, изучающая закономерности случайных событий. Одной из главных задач в теории вероятностей является задача определения количественной меры возможности появления события. 2. Полная группа событий. Пространство элементарных исходов. Примеры. Полная группа событий. Полной группой событий называется совокупность всех возможных результатов опыта. Теорема. Сумма вероятностей событий А1 , А2 , ..., Аn , образующих полную группу, равна единице: Р (A1) + Р (А2) + ... + Р (Аn) = 1. Пространство элементарных исходов Теория вероятностей изучает случайные явления не непосредственно, а с помощью идеализированных математических моделей случайных опытов. Всякий случайный опыт (испытание, эксперимент) состоит в осуществлении некоторого комплекса условий и наблюдении результата. Любой наблюдаемый результат опыта интерпретируется как случайный исход (случайное событие). Случайное событие в результате опыта может произойти, а может и не произойти. Каждому опыту ставится в соответствие пространство элементарных исходов . Это множество простейших (т.е. неразложимых в рамках данного опыта на более простые) взаимоисключающих исходов , таких, что результатом эксперимента всегда является один и только один исход . Пример 1.1.1. Опыт состоит в бросании одной правильной шестигранной игральной кости и наблюдении числа выпавших очков. Элементарные исходы: {выпало очков}, . Неэлементарные исходы (события): ={выпало чётное число очков}, ={выпало число очков, большее, чем 2} и т.п. Исход не является элементарным, т.к. он разлагается на более простые исходы . Пространство элементарных исходов данного случайного опыта состоит из шести элементов. 3. Классическое определение вероятности события. Свойства вероятности события. Примеры. Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных исходов опыта, в котором может появиться это событие. Вероятность события А обозначают через Р (А). В соответствии с определением P(A)=m/n , где m - число элементарных исходов, благоприятствующих событию А; n - число всех равновозможных элементарных исходов опыта, образующих полную группу событий. Это определение вероятности называют классическим. Основные свойства вероятности. Пусть задано пространство элементарных событий Е , а вероятности Р определены на событиях из Е . Тогда: 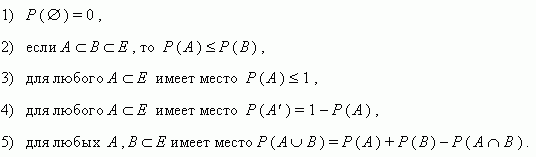 Пример 1. В урне 10 одинаковых по размерам и весу шаров, из которых 4 красных и 6 голубых. из урны извлекается один шар. Какова вероятность того, что извлеченный шар окажется голубым? Решение. Событие "извлеченный шар оказался голубым" обозначим буквой А. Данное испытание имеет 10 равновозможных элементарных исходов, из которых 6 благоприятствуют событию А. В соответствии с формулой P(A)=m/n , получаем P(A)=6/10=0,6 4. Статистическое определение вероятности события. Примеры. Теорема Бернулли (с доказательством). Статистической вероятностью события А называется относительная частота (частость) появления этого события в n произведенных испытаниях, т.е. 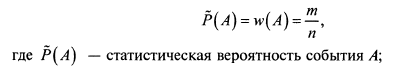 w(A) – относительная частота (частость) события А; m – число испытаний, в которых появилось событие А; n – общее число испытаний. Статистическое определение вероятности, как и понятия и методы теории вероятности, применимы только к тем событиям, которые обладают свойствами:
Пример. Английский учёный Пирсон произвел 23000 бросаний монеты, герб появился 11512 раз. W(A) = 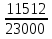 = 0.5005 = 0.5005Теорема Бернулли. Частость события в n повторных независимых испытаниях в каждом из которых оно может произойти с одной и той же вероятностью p, при неограниченном увеличении числа n сходится по вероятности к вероятности р этого события в отдельном испытании: 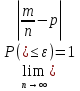 Cмысл теоремы состоит в том, что при большом числе n повторных независимых испытаний практически достоверно, что частость события m/n – величина случайная, как угодно мало отличается от неслучайной величины p – вероятности события, т.е. практически перестает быть случайной. Доказательство:
Отметим, что случайная величина m = 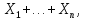 г 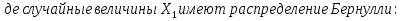 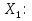 E( 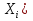 = p ; D( = p ; D(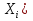 = pq = pqТаким образом, выполняются все условия теоремы Чебышева, т.е. 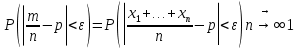 . .5. Геометрическое определение вероятности. Примеры. Классическое определение вероятности основывается на том, что число всех возможных случаев конечно. Если распределение возможных исходов испытания непрерывно и бесконечно, то при решении задач часто используется понятие геометрической вероятности. Полагают, что имеется область Ω и в ней область A. На Ω наудачу бросается точка. Событие А – попадание точки в область А. Геометрической вероятностью события А называется отношение меры области, благоприятствующей появлению события А, к мере всей области Ω, т.е. P(A) = 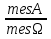 ; ; Область Ω может быть одномерной, двумерной, трехмерной и n-мерной. Пример. В круг радиуса R=50 бросается точка. Найти вероятность ее попадания во вписанный в круг квадрат. Решение. P(A) = 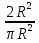 = =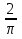 ; ( R = ; ( R = 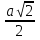 ; a = ; a = 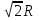 ) )6. Сумма событий и ее свойства. Примеры. Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из данных событий. Если А и В — совместные события, то их сумма А + В обозначает наступление или события А, или события В, или обоих событий вместе. Если А и В — несовместные события, то их сумма А + В означает наступление или события А, или события В. Свойства:
Примеры. 1) Событие А – попадание в цель при первом выстреле, событие В – попадание в цель при втором выстреле, тогда событие С = А + В есть попадание в цель вообще, безразлично при каком выстреле – при первом, при втором или при обоих вместе. 2) Если событие А – появление карты червонной масти при вынимании карты из колоды, событие В – появление карты бубновой масти, то С = А + В есть появление карты красной масти, безразлично – червонной или бубновой. 7. Теорема сложения вероятностей (с доказательством) и ее следствия. Примеры. 8 Произведение событий и его свойства.     9. Условная вероятность. Зависимые и независимые события. Теорема умножения вероятностей (с доказательством). Примеры Вероятность Р(В) как мера степени объективной возможности наступления события В имеет смысл при выполнении определенного комплекса условий. При изменении условий вероятность события В может измениться. Так, если к комплексу условий, при котором изучалась вероятность р(В), добавить новое условие А, то полученная вероятность события В, найденная при условии, что событие А произошло, называется условной вероятностью события В и обозначается РА(В), или Р(В/А), или Р(В/А). Теорема Умножения вероятностей принимает наиболее простой вид, когда события, образующие произведение, независимы. Событие В называется независимым от события А, если его вероятность не меняется от того, произошло событие А или нет, т.е. РА(В)=Р(В) В противном случае, если РА(В) не равно Р(В) событие В называется зависимым от А. Несколько событий А,В,М… называются независимыми в совокупности, если независимы любые два из них и независимо любое из данных событий и любые комбинации (произведения) остальных событий. В противном случае события А,В,М называются зависимыми. Вероятность произведения двух или нескольких независимых событий равна произведению вероятностей этих событий. 10. Формулы полной вероятности и Байеса. Примеры. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ Пусть события H1 , H2 ,K, Hn образуют полную группу попарно несовместных событий. Такие события называются гипотезами. Пусть событие A происходит вместе с гипотезами H1 , H2 ,K, Hn. Тогда для вероятности события A справедлива формула 1 2 n P( A) P(H1 ) PH ( A) P(H2 ) PH ( A) K P(Hn) PH ( A) . Доказательство. A AH1 AH2 K AHn. Так как H1 , H2 ,K, Hnпопарно несовместные, то AH1 , AH2 ,K, AHnтакже попарно несовместные. По правилу сложения вероятностей имеем P( A) P( AHi) P(Hi) PHi( A) . Что и требовалось доказать. Пример. На город примерно 100 дней в году дует ветер с севера и 200 дней в году – с запада. Промышленные предприятия, расположенные на севере, производят выброс вредных веществ каждый третий день, а расположенные на западе – в последний день каждой недели. Как часто город подвергается воздействию вредных выбросов? Решение. Другими словами, нужно вычислить вероятность того, что в наугад выбранный день город будет накрыт промышленным смогом. Обозначим следующие события: A воздействие вредных выбросов, H1 ветер дует с севера, H2 ветер дует с запада. По условию имеем 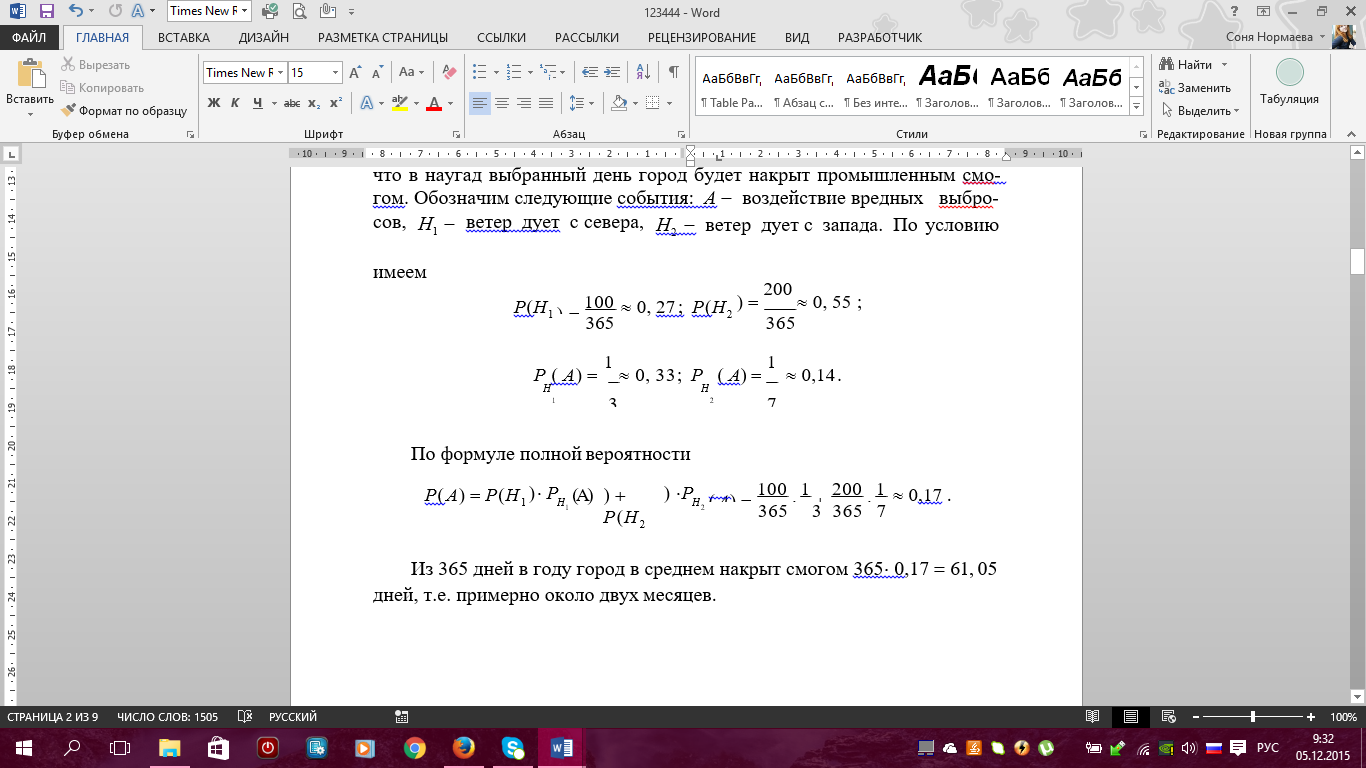 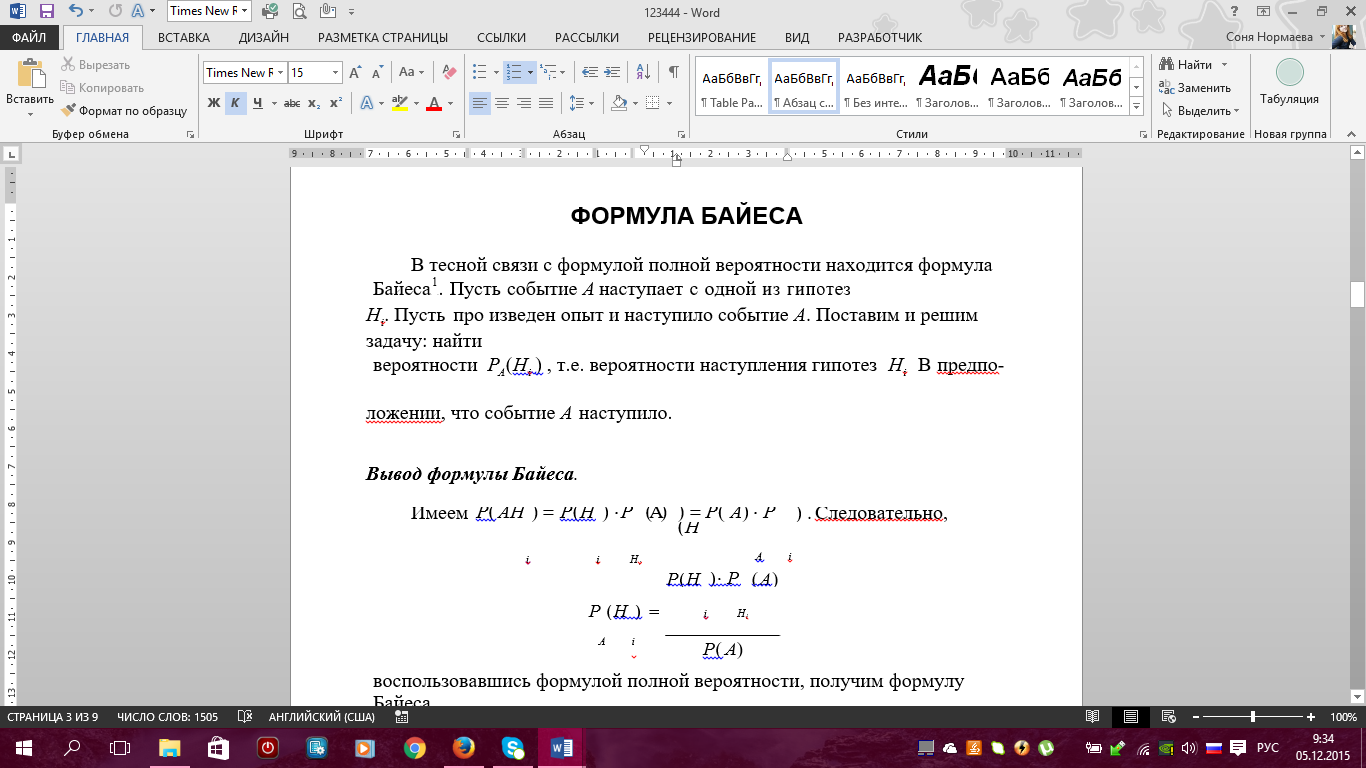 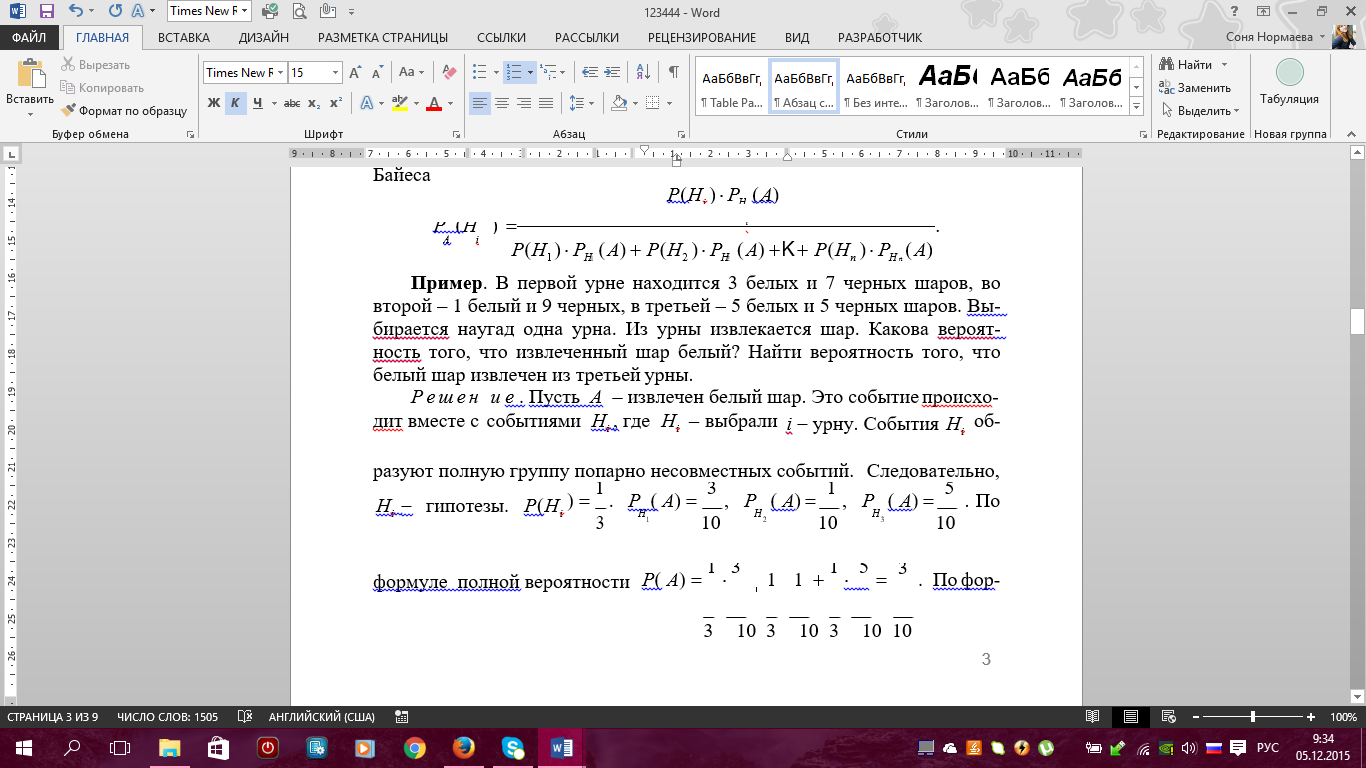 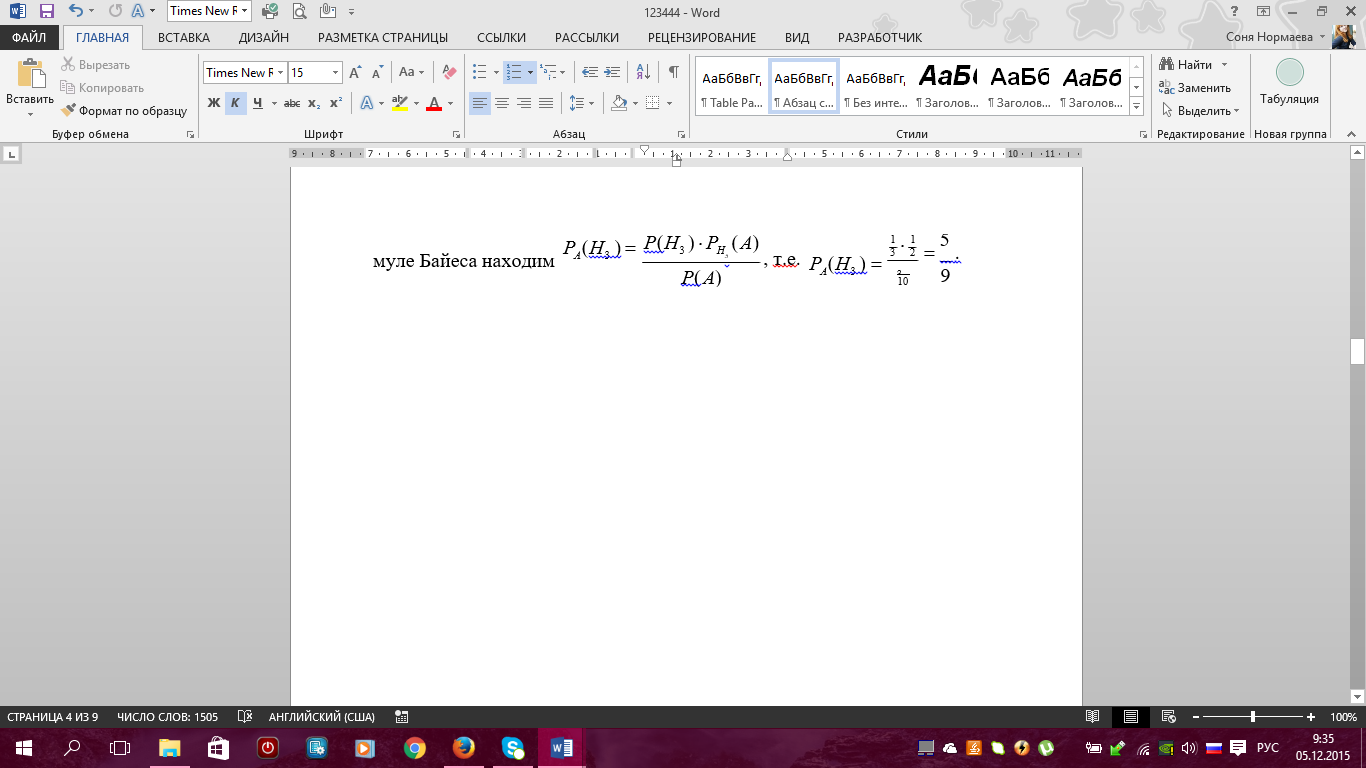 11. Случайная величина (определение). Дискретная случайная величина и ее закон (ряд) распределения. Основное свойство закона распределения. Примеры.  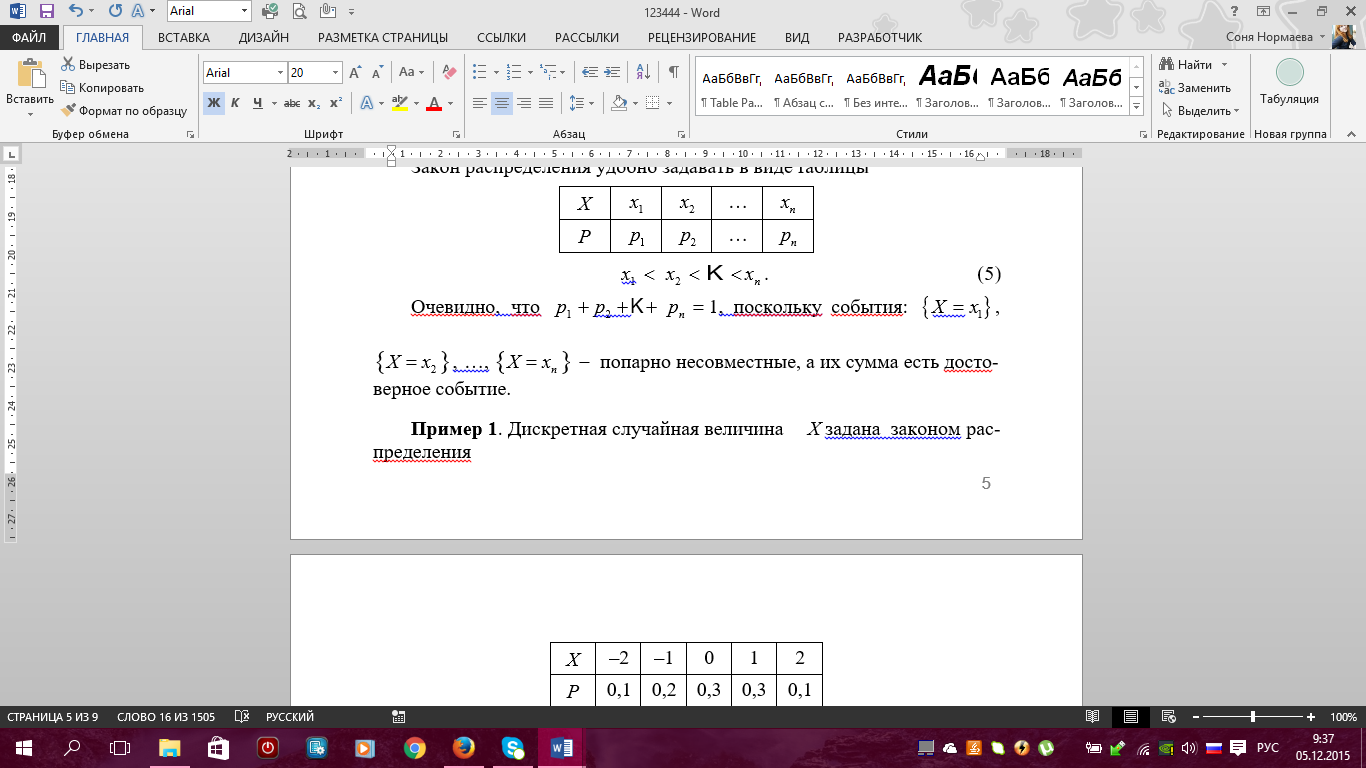 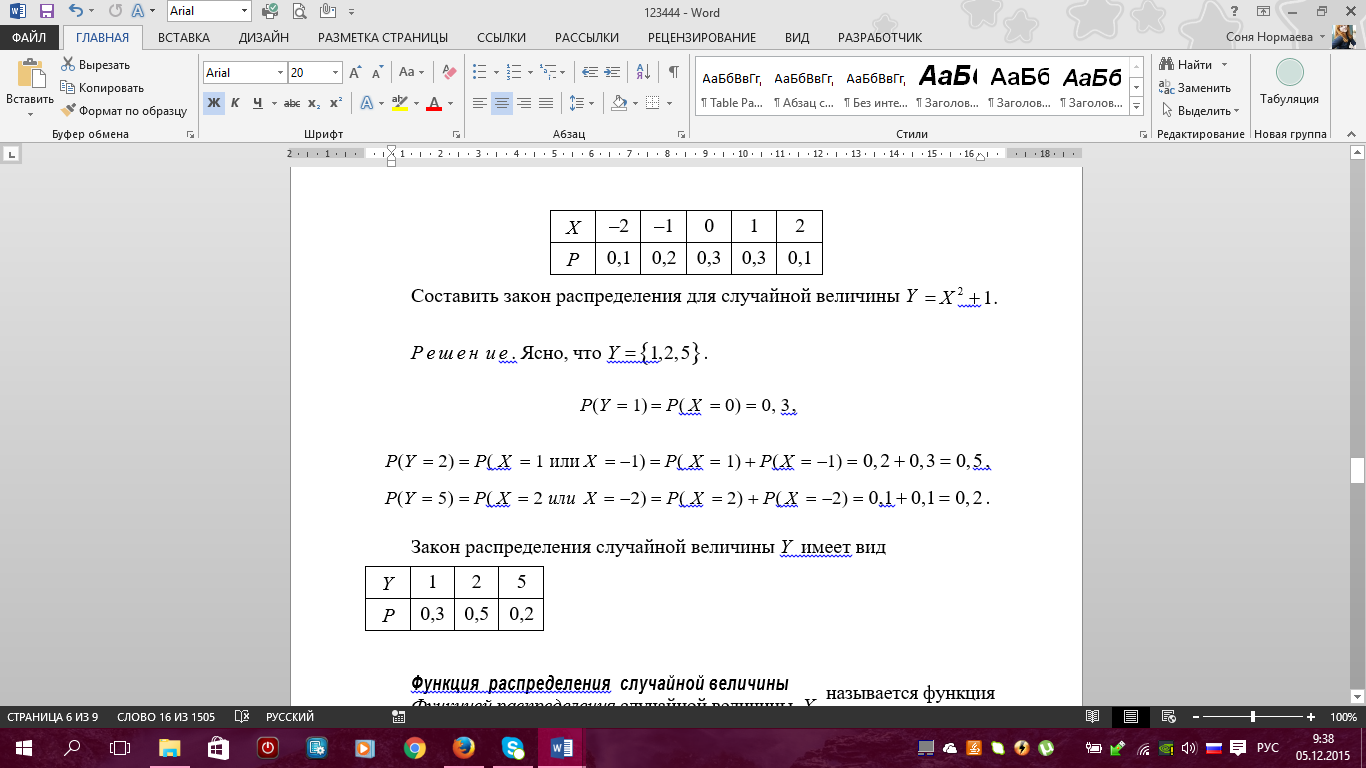 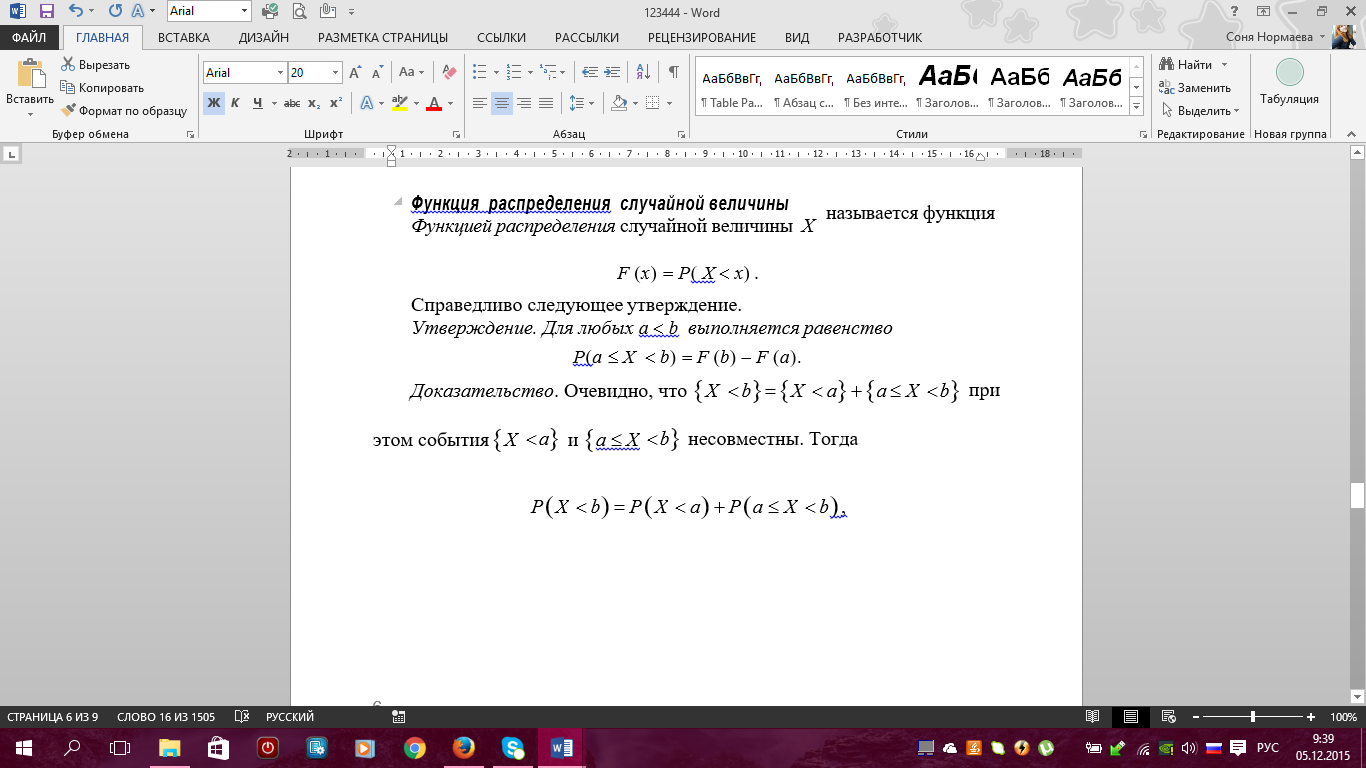 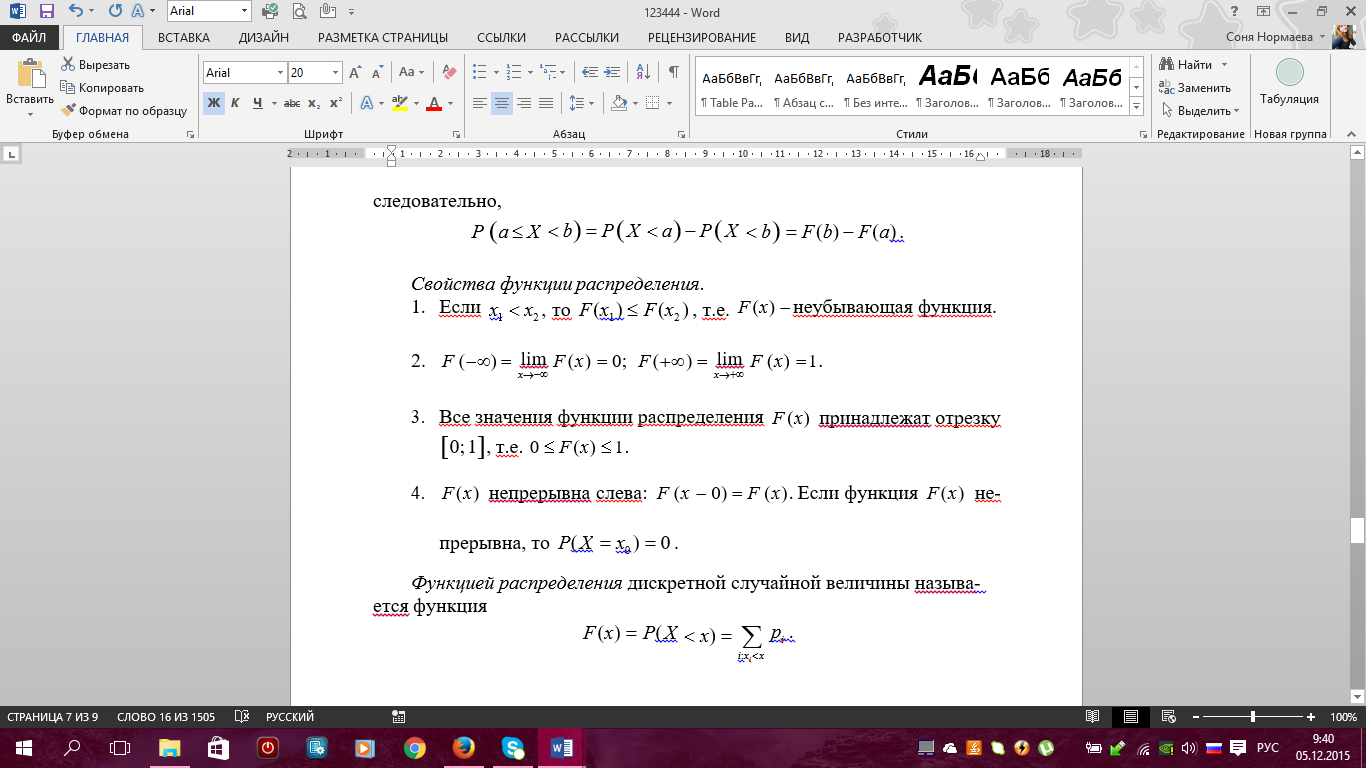 12.* Совместный закон распределения двух дискретных случайных величин. Зависимые и независимые случайные величины. Примеры. Основное свойство совместного закона распределения для независимых случайных величин. |