Быстрый переход:
Определение предела последовательности. Подпоследовательность. Частичный предел.
Критерий Коши. Свойство сходящихся последовательностей. Теорема о пределе промежуточной последовательности.
Определение предела функции. Теорема о пределе промежуточной функции. Первый замечательный предел.
Бесконечно малые функции. Теорема о связи бесконечно малых и бесконечно больших функций.
(+ определение б/б функций limf(x) = ∞)
Теорема о пределе произведения бесконечно малой и ограниченной функции
Второй замечательный предел. Раскрытие неопределенностей 
Сравнение бесконечно малых. Эквивалентность бесконечно малых. Основные эквивалентности.
Теорема о разности эквивалентных бесконечно малых. Теорема о замене эквивалентности в пределе отношения.
Непрерывность функции в точке. Теорема о непрерывности арифметических действий. о непрерывности сложной функции.
Непрерывность функции на отрезке. Свойства функций непрерывных на отрезке.
Точки разрыва и их классификация
Производная, ее геометрический и механический смысл
Теорема о связи непрерывности и дифференцируемости
Арифметические действия с производными
Таблица производных
Производные сложной и обратной функции
Дифференциал, его связь с производной, геометрический смысл, инвариантность.
Теорема Ролля, ее геометрический смысл
Теорема Лагранджа, ее геометрический смысл. Теорема Коши.
Правило Лопиталя.
Многочлен Тейлора, формула Тейлора.
Остаточный член формулы Тейлора в формах Пеано и Лагранджа
Локальный экстремум функции одного переменного. Необходимое и достаточное условия экстремума.
Геометрический смысл второй производной. Точки перегиба.
Асимптоты графика функции. Существование наклонной асимптоты.
Частные производные функции нескольких переменных. Теорема о равенстве смешанных производных.
Дифференцируемость функции нескольких переменных. Дифференциал.
Локальный экстремум функции нескольких переменных. Необходимое условие экстремума.
Нахождение производных по определению 1
Нахождение производных по определению 2
<Справка>
1. Определение предела последовательности. Подпоследовательность. Частичный предел.
Предел числовой последовательности:
Число называется пределом последовательности , если для любого существует номер такой, что для любого выполняется неравенство :

Пусть задана некоторая последовательность { } и есть строго возрастающая последовательность натуральных чисел. Тогда последовательность называется подпоследовательностью последовательности { }.
Будем писать: 
и говорить, что последовательность { } стремится к плюс бесконечности, если для каждого числа найдется номер , такой что при любом Аналогично даются определения для случая ,
Частичный предел последовательности:
Частичным пределом последовательности называется предел какой-нибудь сходящейся подпоследовательности.
Частичным пределом последовательности называется предел какой-либо её подпоследовательности, если существует хотя бы одна подпоследовательность, имеющая предел. В противном случае, говорят, что у последовательности нет частичных пределов.
Пример:
Пусть
Эта последовательность расходится, но ее подпоследовательности и сходятся соответственно к 1 и -1.Таким образом эти числа являются частичными пределами последовательности
<Вернуться назад>
2. Критерий Коши. Свойство сходящихся последовательностей. Теорема о пределе промежуточной последовательности.
Свойства фундаментальных последовательностей:
Если последовательность фундаментальная, тогда существует такой номер , что в -окрестности точки содержатся все члены последовательности, начиная с этого номера.
Последовательность сходится тогда и только тогда, когда она ограниченная и верхний предел равен нижнему.



<Вернуться назад>
3. Определение предела функции. Теорема о пределе промежуточной функции.Первый замечательный предел.

Пределпромежуточной функции
Если имеет место соотношение  и и  , ,  , то и , то и  или говорят: если функция F(х) заключена между двумя функциями s(х) и g(х), стремящимися к одному и тому же пределу, то она также стремится к этому пределу. или говорят: если функция F(х) заключена между двумя функциями s(х) и g(х), стремящимися к одному и тому же пределу, то она также стремится к этому пределу.
Пример: Найти предел функции в точке , если известно, что имеет место соотношение:  и и  , ,
Решение: Найдем пределы заданных функций и при :


А тогда по теореме о предел промежуточной функции и

Ответ. 
Первый замечательный предел:

Так как при α→0 имеем sinα→0, то говорят, что первый замечательный предел раскрывает неопределённость вида 0/0. Вместо переменной α под знаком синуса и в знаменателе может быть расположено любое выражение, если:
Выражения под знаком синуса и в знаменателе одновременно стремятся к нулю, т.е. присутствует неопределенность вида 0/0.
Выражения под знаком синуса и в знаменателе совпадают.
Часто используются также следствия из первого замечательного предела:
<Вернуться назад>
4. Бесконечно малые функции. Теорема о связи бесконечно малых и бесконечно больших функций.
Бесконечно малые функции:
Функция называется бесконечно малой функцией (б.м или б/м) при (или в точке ), если 
Пример:
Функция является бесконечно малой (б.м) функцией при .
Основные свойства бесконечно малых функций:
1)Сумма конечного числа б.м функций является функцией б.м.
2)Произведение б.м функции на ограниченную есть функция б.м.
3)Произведение двух б.м функций есть функция б.м.
4)Произведение б.м функции на константу является б.м функцией.
5)Частное от деления б.м функции на функцию, предел которой не равен 0, есть функция б.м.
6)Функция 1/f(x), обратная к б.м функции, есть функция бесконечно большая. Верно и обратное.
Теорема:
Пусть - предел функции в точке :  . Тогда заданную функцию можно представить в виде . Тогда заданную функцию можно представить в виде  , где - б.м. функция. Верно и обратное утверждение. , где - б.м. функция. Верно и обратное утверждение.
Теорема о связи бесконечно малых и бесконечно больших функций:
Если функция  - функция бесконечно малая ( - функция бесконечно малая ( ), то функция ), то функция  есть бесконечно большая функция и наоборот. есть бесконечно большая функция и наоборот.
Доказательство:
Пусть  - бесконечно малая функция при - бесконечно малая функция при  , т.е. , т.е.  . Тогда для любого числа . Тогда для любого числа  существует такое число существует такое число  , что для всех , что для всех  , удовлетворяющих неравенству , удовлетворяющих неравенству  , выполняется неравенство , выполняется неравенство  , т.е. , т.е. 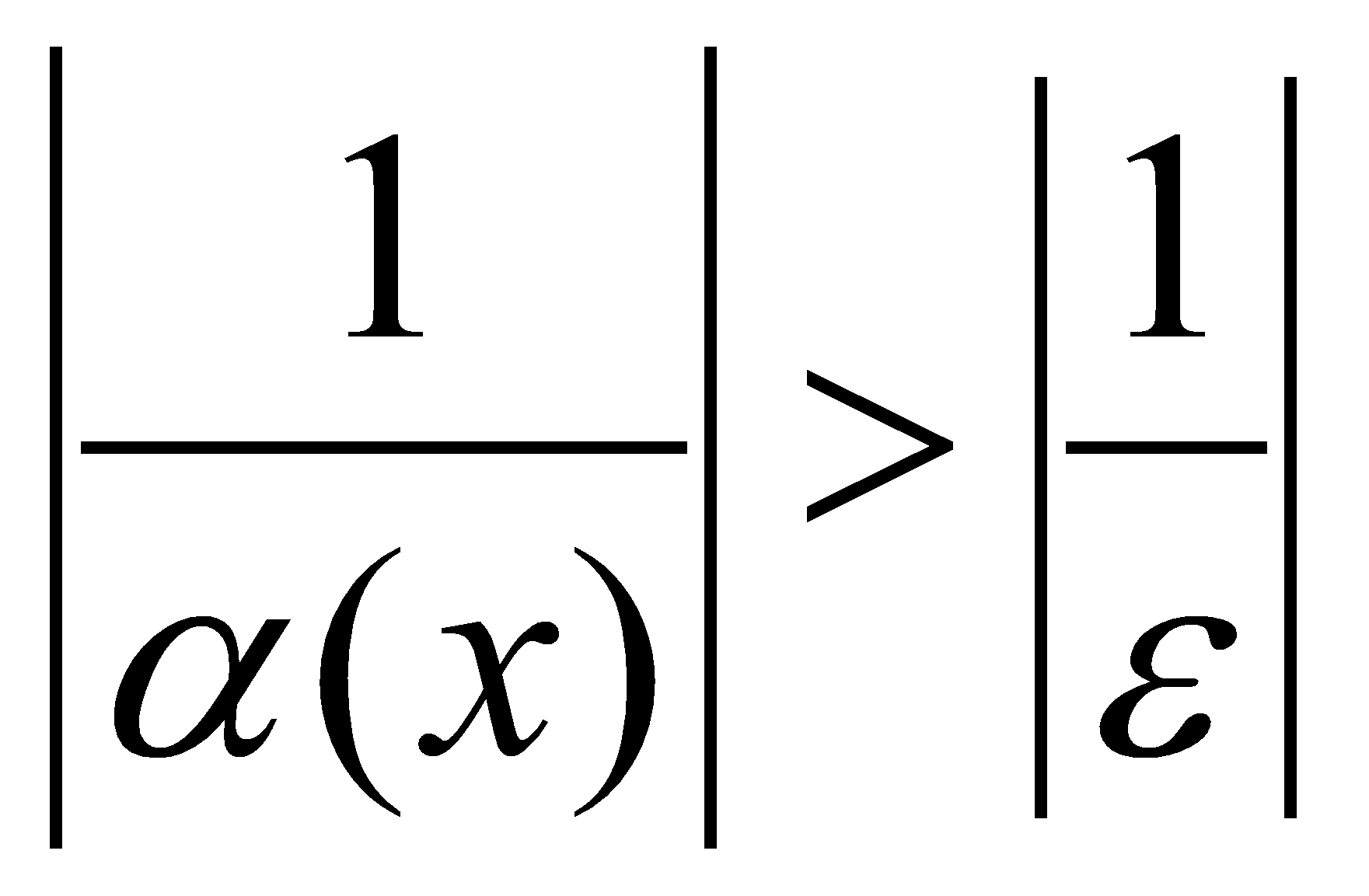 , т.е. , т.е.  , где , где  . А из этого следует, что функция . А из этого следует, что функция  - бесконечно большая. - бесконечно большая.
<Вернуться назад>
5. Теорема о пределе произведения бесконечно малой и ограниченной функции.
Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.
Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a|f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a, то для произвольного ε>0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)|< ε/M. Тогда в меньшей из этих окрестностей имеем | αf|< ε/M= ε. А это и значит, что af – бесконечно малая. Для случая x→∞ доказательство проводится аналогично.
Из доказанной теоремы вытекают:
Следствие 1. Если и , то .
Следствие 2. Если и c=const, то .
<Вернуться назад>
6. Второй замечательный предел. Раскрытие неопределенностей 
Второй замечательный предел:
Второй замечательный предел служит для раскрытия неопределенности 1∞ и выглядит следующим образом:

Обратим внимание на то, что в формуле для второго замечательного предела в показателе степени должно стоять выражение, обратное тому, которое прибавляется к единице в основании (так как в этом случае можно ввести замену переменных и свести искомый предел ко второму замечательному пределу).

<Вернуться назад>
7. Сравнение бесконечно малых. Эквивалентность бесконечно малых. Основные эквивалентности.

Таблица эквивалентных бесконечно малых:
П усть усть  - бесконечно малая при - бесконечно малая при  . .
Эквивалентность всех величин таблицы можно доказать, основываясь на равенстве  . .
<Вернуться назад>
8. Теорема о разности эквивалентных бесконечно малых. Теорема о замене эквивалентности в пределе отношения.
Теорема: Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них.

(См. 7. Сравнение бесконечно малых)
Справедливо и обратное утверждение: если разность б.м.ф. α и ß есть бесконечно малая высшего порядка, чем α или ß, то α и ß — эквивалентные бесконечно малые.
Действительно, так как
 т. е. т. е. 
Отсюда  т. е. α т. е. αß. Аналогично, если то α то α
ß.
Теорема о замене эквивалентности в пределе отношения:
Числитель или знаменатель можно заменить на эквивалентные.
Доказательство: Пусть в точке х = х0 имеем f(x)
α(x). Тогда

<Вернуться назад>
9. Непрерывность функции в точке. Теорема о непрерывностиарифметических действий о непрерывности сложной функции.
Непрерывность функции в точке:
Ф ункция f(x) называется непрерывной в точке ункция f(x) называется непрерывной в точке  , если предел слева равен пределу справа и совпадает со значением функции в точке , если предел слева равен пределу справа и совпадает со значением функции в точке  , то есть: , то есть:
Следствие:
Значение предела функции в точках непрерывности совпадает со значением функции в этих точках.

Теорема о непрерывности сложной функций:
Пусть функция φ(t) непрерывна в точке t0 и функция f(x) непрерывна в точке x0=φ(t0).
Тогда функция f(φ(t)) непрерывна в точке t0.
<Вернуться назад>
10. Непрерывность функции на отрезке. Свойства функций непрерывных на отрезке.
Функция у=ƒ(х) называется непрерывной в интервале (a, b), если она непрерывна в каждой точке этого интервала.
Ф  ункция у=ƒ(х) называется непрерывной на отрезке [а, b], если она непрерывна в интервале (a, b) и в точке х=а непрерывна справа (т.е. ), а в точке x=b непрерывна слева (т. е. ). ункция у=ƒ(х) называется непрерывной на отрезке [а, b], если она непрерывна в интервале (a, b) и в точке х=а непрерывна справа (т.е. ), а в точке x=b непрерывна слева (т. е. ).
Свойства функций непрерывных на отрезке:
Если функция непрерывна на отрезке, то она достигает на этом отрезке свои наибольшее и наименьшее значения (теорема Вейерштрасса).
Непрерывная на отрезке  функция является ограниченной на этом отрезке. функция является ограниченной на этом отрезке.
Если функция  является непрерывной на отрезке является непрерывной на отрезке  и принимает на концах этого отрезка неравные между собой значения, то есть и принимает на концах этого отрезка неравные между собой значения, то есть  , ,  , то на этом отрезке функция принимает и все промежуточные значения между , то на этом отрезке функция принимает и все промежуточные значения между  и и 
(теорема Больцано-Коши).
Если функция  , которая непрерывна на некотором отрезке , которая непрерывна на некотором отрезке  , принимает на концах отрезка значения разных знаков, то существует такая точка , принимает на концах отрезка значения разных знаков, то существует такая точка  такая, что такая, что  . .
<Вернуться назад>
1 1. Точки разрыва и их классификация. 1. Точки разрыва и их классификация.
<Вернуться назад>
12. Производная, ее геометрический и механический смысл.
Производная равна пределу отношения приращения функции к приращению аргумента, при условии, что последний стремится к нулю:


или
Функция, которая имеет конечную производную в некоторой точке, называется дифференцируемой в данной точке. Процесс вычисления производной называется дифференцированием функции.
Геометрический смысл производной:
Производная функции , вычисленная при заданном значении , равна тангенсу угла, образованного положительным направлением оси и положительным направлением касательной, проведенной к графику этой функции в точке с абсциссой :


Замечание: Геометрически производная представляет собой угловой коэффициент касательной к графику функции в точке .
Механический смысл производной:
Пусть задан путь движения материальной точки. Скорость данной материальной точки в момент времени есть производная от пути по времени :
<Вернуться назад>
13.Теорема о связи непрерывности и дифференцируемости.
Если функция дифференцируема в точке, то она непрерывна в этой точке.
Доказательство:
Пусть функция у=f(x) дифференцируема в точке х0. Дадим в этой точке аргументу приращение Dх. Функция получит приращение Dу.

Найдем
Следовательно, у=f(x) непрерывна в точке х0.
Следствие. Если х0 – точка разрыва функции, то в ней функция не дифференцируема.
Утверждение, обратное теореме, не верно. Из непрерывности не следует дифференцируемость.
П ример: ример:
у=|х|, х0=0.
Dх>0, ;
Dх<0, .
В точке х0=0 функция непрерывна, но производной не существует.
<Вернуться назад>
14. Арифметические действия с производными.

<Вернуться назад>
15.Таблица производных.

<Вернуться назад>
16. Производные сложной и обратной функции.
Таблица производных сложной функции:

Производная обратной функции:
Если y=f(x) и x=g(y) — пара взаимно обратных функций, и функция y=f(x) имеет производную f'(x), то производная обратной функции g'(x)=1/f'(x).
Доказательство:
По условию теоремы функция x = f(y) монотонна и дифференцируема, следовательно, по теореме о существовании обратной функции функция у = f--1(x) существует, монотонна и непрерывна на соответствующем интервале. Дадим аргументу х приращение Δх¹0. Тогда функция у = f--1(x) получит приращение Δу, которое в силу ее монотонности отлично от нуля. Так как функция у = f--1(x) непрерывна, то Δу®0 при Δх®0.

Тогда
<Вернуться назад>
17.Дифференциал, его связь с производной, геометрический смысл, инвариантность.
Дифференциалом  в точке x, соответствующему в точке x, соответствующему  называется главная линейная часть приращения функции. называется главная линейная часть приращения функции.  . .
То есть если существует производная, то  при при  , и дифференциал , и дифференциал  . Когда x=const, то переменной является . Когда x=const, то переменной является  и дифференциал будет линейной функцией. и дифференциал будет линейной функцией.
геометрический смысл дифференциала: дифференциал функции  в точке равен приращению ординаты касательной к графику функции в этой точке, когда получит приращение в точке равен приращению ординаты касательной к графику функции в этой точке, когда получит приращение
Инвариантность формул первого дифференциала
Пусть существует сложная функция  , и существует ее производная: , и существует ее производная:  . Считая y независимой переменной, получим формулу дифференциала: . Считая y независимой переменной, получим формулу дифференциала:  . Теперь, если считать y зависимой от x, получим: . Теперь, если считать y зависимой от x, получим:  , т.к. , т.к.  . То есть получается, что формула дифференциала не зависит от типа переменной. . То есть получается, что формула дифференциала не зависит от типа переменной.
<Вернуться назад>
18. Теорема Ролля, её геометрический смысл.
Пусть функция f (x) непрерывна на [a, b], дифференцируема на (a, b) и на концах отрезка принимает равные значения f(a) = f(b). Тогда существует точка c Î (a, b), в которой f ' (c) = 0.
Доказательство. Так как функция f(x) непрерывна на [a, b], то по свойству непрерывных функций она достигает на этом отрезке максимальное значение М и минимальное значение m. Возможны два случая: максимум и минимум достигаются на концах отрезка или что – либо (или максимум, или минимум) попадает вовнутрь интервала. В первом случае f (x) = const = M = m. Поэтому производная равна нулю f ' (c) = 0 в любой точке отрезка [a, b], и теорема доказана. Во втором случае, так как f (x) дифференцируема в точке c, из теоремы Ферма следует, что f ' (c) = 0.
Геометрически теорема Ролля означает, что у графика непрерывной на отрезке [a, b] и дифференцируемой внутри этого отрезка функции, принимающей на его концах f(a) = f(b) равные значения, существует точка (c; f(c)), в которой касательная параллельна оси Оx.

<Вернуться назад>
19. Теорема Лагранджа, ее геометрический смысл. Теорема Коши.
Пусть функция дифференцируема в открытом промежутке и сохраняет непрерывность на концах этого промежутка. Тогда существует такая точка , что
|

|
(13)
|
|
Доказательство. Рассмотрим вспомогательную функцию

Эта функция непрерывна и дифференцируема в промежутке , а на его концах принимает одинаковые значения:

Тогда удовлетворяет всем условиям теоремы Ролля и, следовательно, существует точка , в которой производная функции равна нулю:

Геометрическая интерпретация теоремы Лагранжа. Разностное отношение в правой части формулы (13) есть угловой коэффициент секущей, проходящей через точки и , а производная равна угловому коэффициенту касательной к графику функции в некоторой средней точке промежутка . Поэтому за теоремой Лагранжа закрепилось название “теорема о среднем”.

Теорема Коши. Пусть функции и непрерывны в замкнутом промежутке ; дифференцируемы в открытом промежутке ; в открытом промежутке . Тогда существует такая точка , что
Доказательство. Заметим, что  . В противном случае – согласно теореме Ролля – производная обратилась бы в нуль в некоторой точке . . В противном случае – согласно теореме Ролля – производная обратилась бы в нуль в некоторой точке .
Рассмотрим вспомогательную функцию

которая удовлетворяет всем условиям теоремы Ролля и, в частности, принимает одинаковые значения на концах промежутка :

Тогда существует точка , в которой

что и требовалось доказать.
<Вернуться назад>
20. Правило Лопиталя.
Первое правило Лопиталя
Рассмотрим функции , которые бесконечно малЫв некоторой точке . Если существует предел их отношений , то в целях устранения неопределённости можно взять две производные – от числителя и от знаменателя. При этом: , то есть при дифференцировании числителя и знаменателя значение предела не меняется.
Примечание: предел тоже должен существовать, в противном случае правило не применимо.
Второе правило Лопиталя
Брат-2 борется с двумя спящими восьмёрками . Аналогично:
Если существует предел отношения бесконечно большихв точке функций: , то в целях устранения неопределённости можно взять две производные – ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. При этом: , то есть при дифференцировании числителя и знаменателя значение предела не меняется.
Примечание: предел должен существовать
Опять же, в различных практических примерах значение может быть разным, в том числе, бесконечным. Важно, чтобы была неопределённость .
<Вернуться назад>
21. Многочлен Тейлора, формула Тейлора.
Рассмотрим многочлен -й степени

Его можно представить в виде суммы степеней , взятых с некоторыми коэффициентами. Продифференцируем его раз по переменной , а затем найдем значения многочлена и его производных в точке :





Таким образом, получаем, что

Полученное выражение называется формулой Маклорена для многочлена степени .
Рассуждая аналогично, можно разложить многочлен по степеням разности , где - любое число. В этом случае будем иметь:

Это выражение называется формулой Тейлора для многочлена в окрестности точки .
Пример
Задание. Разложить в ряд Тейлора функцию  в точке . в точке .
Решение. Найдем производные:



Итак,  , ,  , . Значение функции в точке , . Значение функции в точке

Таким образом,


Ответ. 
Для произвольной функции , не являющейся многочленом, формула Тейлора в окрестности некоторой точки принимает вид:

Последнее слагаемое  называется остаточным членом в форме Пеано. называется остаточным членом в форме Пеано.
Замечание
Формула Маклорена является частным случаем формулы Тейлора при .
<Вернуться назад>
22. Остаточный член формулы Тейлора в формах Пеано и Лагранжа.
Формула Тейлора с остаточным членом в форме Пеано. Пусть функция f: [a, b] → R имеет в точке x0 производную n-го порядка. Тогда при x → x0

Если x0 = a или x0 = b, то под производными понимаются соответствующие односторонние производные.
Формула Тейлора с остаточным членом в форме Лагранжа имеет вид

<Вернуться назад>
23. Локальный экстремум функции одного переменного. Необходимое и достаточное условия экстремума.
Определение
Точка называется точкой локального максимума функции , если существует такая окрестность этой точки, что для всех из этой окрестности выполняется неравенство:  . .
Точка называется точкой локального минимума функции , если существует такая окрестность этой точки, что для всех из этой окрестности  . .
Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.
Замечание
Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.
Теорема
(Необходимое условие экстремума)
Если функция имеет экстремум в точке , то ее производная либо равна нулю, либо не существует.
Точки, в которых производная равна нулю: , называются стационарными точками функции.
Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются критическими точками этой функции. То есть критические точки - это либо стационарные точки (решения уравнения ), либо это точки, в которых производная не существует.
Замечание
Не в каждой своей критической точке функция обязательно имеет максимум или минимум.
Теорема
(Первое достаточное условие экстремума)
Пусть для функции выполнены следующие условия:
функция непрерывна в окрестности точки ;
или не существует;
производная при переходе через точку меняет свой знак.
Тогда в точке функция имеет экстремум, причем это минимум, если при переходе через точку производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку производная меняет свой знак с плюса на минус.
Если производная при переходе через точку не меняет знак, то экстремума в точке нет.
Таким образом, для того чтобы исследовать функцию на экстремум, необходимо:
найти производную ;
найти критические точки, то есть такие значения , в которых или не существует;
исследовать знак производной слева и справа от каждой критической точки;
найти значение функции в экстремальных точках.
Пример
Задание. Исследовать функцию  на экстремум. на экстремум.
Решение. Находим производную заданной функции:

Далее ищем критические точки функции, для этого решаем уравнение :

Первая производная определена во всех точках. Таким образом, имеем одну критическую точку . Наносим эту точку на координатную прямую и исследуем знак производной слева и справа от этой точки (для этого из каждого промежутка берем произвольное значение и находим значение производной в выбранной точке, определяем знак полученной величины):

Так как при переходе через точку производная сменила свой знак с "-" на "+", то в этой точке функция достигает минимума (или минимального значения), причем  . .
Замечание. Также можно определить интервалы монотонности функции: так как на интервале производная , то на этом интервале функция  является убывающей; на интервале производная , значит заданная функция возрастает на нем. является убывающей; на интервале производная , значит заданная функция возрастает на нем.
Ответ. 
Теорема
(Второе достаточное условие экстремума)
Пусть для функции выполнены следующие условия:
она непрерывна в окрестности точки ;
первая производная в точке ;
 в точке . в точке .
Тогда в точке достигается экстремум, причем, если  , то в точке функция имеет минимум; если , то в точке функция имеет минимум; если  , то в точке функция достигает максимум. , то в точке функция достигает максимум.
<Вернуться назад>
24. Геометрический смысл второй производной. Точки перегиба.
Теорема
(Об условиях выпуклости или вогнутости графика функции)
Пусть функция определена на интервале и имеет непрерывную, не равную нулю в точке вторую производную. Тогда, если всюду на интервале , то функция имеет вогнутость на этом интервале, если , то функция имеет выпуклость.
Определение
Точкой перегиба графика функции называется точка  , разделяющая промежутки выпуклости и вогнутости. , разделяющая промежутки выпуклости и вогнутости.
Теорема
(О необходимом условии существования точки перегиба)
Если функция имеет перегиб в точке  , то или не существует. , то или не существует.
Теорема
(О достаточном условии существования точки перегиба)
Если:
первая производная непрерывна в окрестности точки ;
вторая производная или не существует в точке ;
при переходе через точку меняет свой знак,
тогда в точке  функция имеет перегиб. функция имеет перегиб.
|
 Скачать 2.1 Mb.
Скачать 2.1 Mb.















 . А из этого следует, что функция
. А из этого следует, что функция 


 усть
усть  .
.


 1. Точки разрыва и их классификация.
1. Точки разрыва и их классификация.


 ример:
ример:



