Высш мат. Решение ду. Опред
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
1.Основные понятия теории ДУ. ДУ первого порядка. Формулировка теоремы существования и единственности решения задачи Коши. Общее, частное и особое решение ДУ. Опред. Диф.наз. уравнение связывающее независимую переменную х , искомую функцию y=ƒ(х) и её производные ƒ’(х), ƒ’’(х)… ƒn(х) или дифференциалы df, d2f…dnf. ДУ в общем виде можно записать так: F(x;y;y';у’’…yn)=0. Если искомая функция y=ƒ(х), есть функция одного аргумента, то ДУ наз. обыкновенным. Если функция u=f(x,y,z…t) зависит от двух и большего числа аргументов, будет содержать функц.частн.производных, такое уравн. носит наз. ДУ в частных производных. 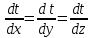 Опред.Порядком ДУ наз. Порядок наивысшей производной входящей в ДУ. Опред. Общим решением ДУ порядка nназ. функц. y=f(х,C1,C2,…,Cn ) зависящая от х и от произвольных постоянных C1,C2,…,Cn обращающая это уравнение в тождество или равенство. Общее решение заданое в неявном виде F(х,C1,C2,…,Cn)=0. При любом наборе конкретных постоянных C1,C2,…,Cnполучаются частные решения. На практике частные решения получают из общего с учётом тех условий которым должно удовлетворять искомое частн. решение, задание таких условий наз. заданием начальных условий и записывается кратко так: f(x0)=y0, f’(x0)=y’0 … fn-1(x0)=yn-10 Задача нахождения частн. решения удовлетв. начальным условиям наз. задачей Коши Среди ДУ встречаются такие, которые имеют решения не получающиеся из общего решения ни при каких значения С , такие решения наз. особыми. Опред. ДУ 1-го порядка связывает независимую переменную х, искомую функцию y=ƒ(х) и её первую производную ƒ’(х) F(x;y;y')=0. Если уравнение можно разрешить относительно y', то его записывают в виде у'=ƒ(х;у) – ДУ 1-го порядка разрешенное относительно производной При нахождении решения приходится в большинстве случаев выполнять операции интегрирования, поэтому процесс нахождения решения ДУ наз. Интегрированием ДУ. График решения ДУ наз. интегральной кривой. Условия при которых ДУ имеет решения составляют содержания основной теоремы теорииДУ Теорема Коши Если правая часть ƒ(х;у) ДУ и ее частная производная ƒ’y(х;у) определены и непрерывны в некоторой области D изменения переменных х и y, то какова бы ни была внутренняя точка(х0,у0)эD данное уравнение имеет единственное решение y= фи(х) принимающие при х=х0 заданное значение y=y0 Геометрически это означает, что через каждую внутреннюю точку (х0,у0)эD Проходит единственная интегральная кривая. Опред. Функция y= фи(х, С) зависящая от аргумента х и произвольной постоянной С наз. общим решением уравнения у'=ƒ(х;у) в области D, если она удовлетворяет двум условиям: При любых значения произв. постоянной С принадлеж. некоторому множеству функции y= фи(х, С) явл. Решением уравнения у'=ƒ(х;у) Какова бы ни была внутренняя т.(х0,у0)эD, существ. Единственное значение С=С0 такое, что решение y=f(x, C0) удовлетв. нач. условию.Опред.Чacтным решением ДУ первого порядка называется любая функция у= фи(х, С0), полученная из общего решения у=фи(х;С) при конкретном значении постоянной С=С0 2. Дифференциальные уравнения первого порядка с разделяющими переменными Дифференциальные уравнения первого порядка в общем виде можно записать либо через производные F(x,y,y’)=0, либо через дифференциалы. Дифференциальное уравнение- уравнение с разделяющимися переменными, если его можно представить в виде: P(x)dx+Q(у)dy=0. Уравнение будет уравнением с разделяющимися переменными, если его можно преобразовать так, чтобы в одной его части была только одна переменная, а в другой – только другая. Замечание 1 При проведении почленного деления ДУ на Q (у) *Р (х)могут быть потеряны некоторые решения. Поэтому следует отдельно решить уравнение Q(у)*P(x)=0 и установить те решения .ДУ, которые не могут быть получены из общего решения, - особые решения. 2. Уравнение У' = f1(Х) . f2(Y) также сводится к уравнению с разделёнными переменными. Для этого достаточно положить у' = dy/dx и разделить переменные . 3.Уравнение У' = f(ax + bу + с), где а, Ь, с - числа, путем замены ах + bу + с = u сводится к ДУ с разделяющимися переменными. Затем интегрируем и заменяем u на ах + bу + с, получим общий интеграл исходного уравнения. 3.Однородные дифференциальные уравнения первого порядка ДУ 1-ого порядка наз. однородным, если его можно представить у’=φ ( 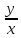 ), где правая часть есть функция, только степенного отношения переменных ), где правая часть есть функция, только степенного отношения переменных 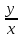 . .Однородное уравнение преобразуют в уравнение с разделяющимися переменными при помощи замены переменной:  =u или у=u*x. =u или у=u*x.Однородное уравнение часто задают в дифференциальной форме: P(x;y)*dx+Q(x;y)*dy=0 (1). ДУ (1) будет однородным , если P(x;y) и Q(x;y) – однородные функции одинакового порядка. Переписав уравнение (1) в виде 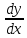 = - = - 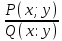 и применив в правой части рассмотренное выше преобразование, получим уравнение у’=φ ( и применив в правой части рассмотренное выше преобразование, получим уравнение у’=φ (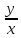 ). ).4.Линейные дифференциальные уравнения 1-го порядка Уравнение вида 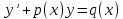 (1) , где p(x) и q(x) непрерывные функции, называются линейными ДУ 1-го порядка. (1) , где p(x) и q(x) непрерывные функции, называются линейными ДУ 1-го порядка. Если 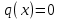 , то уравнение (1) называется линейным однородным ДУ 1-го порядка. Если , то уравнение (1) называется линейным однородным ДУ 1-го порядка. Если 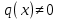 , то уравнение (1) называется линейным неоднородным ДУ 1-го порядка. , то уравнение (1) называется линейным неоднородным ДУ 1-го порядка.Для нахождения решения уравнения (1) может быть применен метод подстановки Бернулли. Рассмотрим метод подстановки Бернулли. Решение будем искать в виде 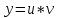 , где , где  , , 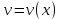 – неизвестные функции от х, причем одна их них произвольна. Тогда – неизвестные функции от х, причем одна их них произвольна. Тогда 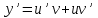 . Подставив выражения для y и y’ в уравнение (1), будем иметь: . Подставив выражения для y и y’ в уравнение (1), будем иметь: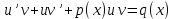 или или 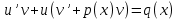 (2). (2). В качестве 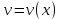 возьмем одно из решений уравнения возьмем одно из решений уравнения 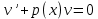 - уравнение с раздел.переменными. Разделяя переменные, получим: - уравнение с раздел.переменными. Разделяя переменные, получим: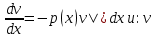 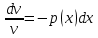  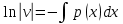 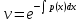 Подставив найденную функцию v в равенство (2), будем иметь: 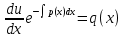 . .Умножаем на dx: 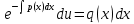 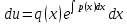 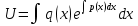 Перемножив найденные функции 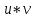 , мы и найдем общее решение уравнения (1). , мы и найдем общее решение уравнения (1). 5. Диф-ные ур-я 2-го порядка, допускающие понижение порядка. Методы решения Рассмотрим диф. ур-я 2-го порядка допускающее понижение порядка. Простейшими уравненими 2-го порядка допускающими понижение пор-ка явл-ся:y’’ = f (x) (1) y’’ = f (x,y)’ (2) y’’ = f (y,y’) (3) Рассмотрим уравнение (1) Введём новую ф-ю U(x), полагая y’ = U(x).Тогда y” = U’(x) и уравнение (3) примет вид:U’(x) = f(x) Решая это уравнение получим:y’= ∫ f(x)dx + C1 Интегрируя его,мы находим общее решение уравнения (1): y = ∫(∫ f(x)dx) + C1x +C2 Рассмотрим уравнение (2) Это ур-е не содержит в явном виде ф-ции у .Вводя новую ф-ю р(х) = у’ и замечая,что y”= p’(x) , получаем уравнение 1-го порядка относительно функции р(х): p’(x)= f(x, p(x)) Допустим,что найдено общее решение р= ᵠ(х, С1).Заменяя в этом решении ф-ю р на y’получаем y’ = (x, C1) Общее решение ур-я (2) имеет вид: у = ∫ ᵠ(х, С1)dx + С2 Рассмотрим уравнение (3) Это ур-ние не содержит явно переменной х. Для понижения порядка снова вводим новую ф-ю р(у) , зависящую от переменной у, полагая y’ = p(y) Дифференцируя это равенство по перменной х учитываем,что у является ф-ей от х:y” = dp(y)/dx = dp(y)/dy * dy/dx Так ка dy/dx = p(x) , то y” = dp/dy *p Подставляя в выражение для у’и y” в уравнение (3) получаем диф. Ур-ние 1-го порядка относительно ф-ции р(у): dp/dy *p = f(y, p(y)) Пусть ф-ция р(у) = f(у, С1) явл-ся решением этого уравнения Учитывая dy/dx = p(y) получим уравнение с разделяющимися переменными dy/dx = ᵠ(y, C1) Разделяя переменные и интегрируя его ,находим общий интера уравнения (3): ∫dy/ ᵠ(y, C1 ) = x+C1 6.Линейные дифференциальные уравнения второго порядка . Общие понятия. Опр. Дифференциальные уравнения вида a0(x)y″+а1(х)y′+ а2(х)y=b(x)(1),где a0(x),а1(х), а2(х)и свободный член b(x)-заданные функции аргумента х называются линейным дифференциальным уравнением второго порядка .Если свободный член b(x)≡0,то линейное уравнение принимает вид a0(x)y″+а1(х)y′+ а2(х)y=0(2) и называется однородным дифференциальным уравнением второго порядка .Если b(x)≠0,то уравнение называется неоднородным линейным дифференциальным уравнением второго порядка .Разрешим уравнение (1) относительно y″= 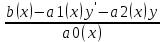 (3) т.к это уравнение является частным видом дифференциального уравнения y″=f(x,y,y′),то для него справедлива теорема существования и единственности решения сформулированная на прошлой лекции .Однако для линейного уравнения эта теорема может быть сформулирована проще . Допустим что коэффициенты уравнения a0(x),а1(х), а2(х) и свободный член b(x) непрерывные в некотором интервале (ᵅ,ᵝ)при чем а0(х)≠0 ни в одной точке этого интервала ,тогда правая часть уравнения (3) f(x,y,y′)= (3) т.к это уравнение является частным видом дифференциального уравнения y″=f(x,y,y′),то для него справедлива теорема существования и единственности решения сформулированная на прошлой лекции .Однако для линейного уравнения эта теорема может быть сформулирована проще . Допустим что коэффициенты уравнения a0(x),а1(х), а2(х) и свободный член b(x) непрерывные в некотором интервале (ᵅ,ᵝ)при чем а0(х)≠0 ни в одной точке этого интервала ,тогда правая часть уравнения (3) f(x,y,y′)=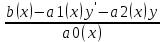 и её частные производные fy′(x,y,y′)=- и её частные производные fy′(x,y,y′)=-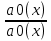 ; fy′′(x,y,y′)=- ; fy′′(x,y,y′)=- являются непрерывными функциями при любых значениях х€(ᵅ,ᵝ).На основании сказанного сформулируем теорему существования и единственности решения линейного дифференциального уравнения (1) Теорема: Если коэффициенты a0(x),а1(х), а2(х) и правая часть b(x) линейного уравнения (1) непрерывна в интервале (ᵅ,ᵝ),причём коэффициент а0(х)≠0 ни в одной точке этого интервала ,то каковы бы ни были начальные условия y(x0)=y0, y′(x0)=y0′,где х0€(ᵅ,ᵝ) существует единственное решение удовлетворяющее данным начальным условиям . являются непрерывными функциями при любых значениях х€(ᵅ,ᵝ).На основании сказанного сформулируем теорему существования и единственности решения линейного дифференциального уравнения (1) Теорема: Если коэффициенты a0(x),а1(х), а2(х) и правая часть b(x) линейного уравнения (1) непрерывна в интервале (ᵅ,ᵝ),причём коэффициент а0(х)≠0 ни в одной точке этого интервала ,то каковы бы ни были начальные условия y(x0)=y0, y′(x0)=y0′,где х0€(ᵅ,ᵝ) существует единственное решение удовлетворяющее данным начальным условиям .9. ЛОДУ 2ого порядка с постоянными коэффициентами. Д.у. вида y”+py’+q=0 (6), где p и q –действительные числа, называется линейным однородным дифференциальным уравнением 2ого порядка с постоянными коэффициентами. Теорема1. Если число k является корнем уравнения k2+pk+q=0 (7), то функция y=ekx является решением уравнения (6). Доказательство: Пусть y=ekx, где k- константа, тогда y’=kekx, y”= k2ekx. Подставляя выражение для y,y’,y” в уравнение (6), получим: k2ekx+pkekx+qekx=0 ekx(k2+pk+q)=0 Уравнение (7) называется характеристическим уравнением данного уравнения (6). Характеристическое уравнение (7) является квадратным уравнением, имеющим 2 корня. Обозначим их через k1 и k2. Теорема2.Общее решение уравнения (6) может быть записано следующим образом: Если корни характеристического уравнения действительные и различные, то общее решение имеет вид: y=C1ek1x+C2ek2x(8) Если корни характеристического уравнения действительные и равные, то общее решение имеет вид: y=C1ek1x+C2xek1x y”2= 2k1ek1x+ xk12ek1x Подставляем выражение для y2, y’2, y”2 в левую часть уравнения (6), получим: xk12ek1x+ 2k1ek1x+ p(ek1x++ xk1ek1x) + qxek1x= ek1x(x(k12 +pk1 +q) + (2k1 + p)) = ek1x(x(k12 +pk1 +q) + (2k1 + 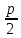 ))=0 ))=0Т.к. k1 – корень характеристического уравнения и значит k12+pk1+q=0. K1=k2= 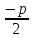 , поэтому k1+ , поэтому k1+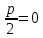 . Следовательно, функция y2=xek1x является 2ым частным решением уравнения(6). Решения y1 и y2 – линейно независимы, т.к. . Следовательно, функция y2=xek1x является 2ым частным решением уравнения(6). Решения y1 и y2 – линейно независимы, т.к.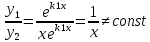 и по т-ме о структуре общего решения ЛОДУ 2ого порядка, общее решение уравнения (6) имеет вид: : y=C1ek1x+C2xek1x. и по т-ме о структуре общего решения ЛОДУ 2ого порядка, общее решение уравнения (6) имеет вид: : y=C1ek1x+C2xek1x.Если корни характеристического уравнения комплексные, k1= α+iβ, k2= α- iβ то общее решение имеет вид: y=eαx(C1cosβx +C2sinβx) Доказательство: Пусть k1 и k2– комплексно-сопряженные, т.е. k1= α+iβ, k2= α- iβ (β≠0) , тогда по т-ме1 ф-ции y1=ek1x=e(α+iβ)x, y2=ek2x=e(α-iβ)x являются частными решениями уравнения (6). Общее решение будет иметь вид: y=Ϛ1ek1x+Ϛ2ek2x= Ϛ1e(α+iβ)x + Ϛ2e(α-iβ)xилиy=eαx(Ϛ1eiβx + Ϛ2e-iβx). Применяя формулу Эйлераe iα=cosϕ+isinϕ, получим: y = eαx(Ϛ1(cosβx +isinβx)+ Ϛ2(cosβx -isinβx))= eαx((Ϛ1+ Ϛ2)cosβx +i(Ϛ1- Ϛ2) sinβx) Обозначив Ϛ1+ Ϛ2=C1, i(Ϛ1- Ϛ2)=C2, получим окончательный вид общего уравнения (6): y=eαx(C1cosβx +C2sinβx). 10.Линейные неоднородные Д.У. второго порядка.Теорема о структуре их общего решения Рассмотрим ЛНДУ 2-го порядка: y”+p(x)y’+q(x)y=f(x) (1) Имеет место теорема о структуре общего решения ЛНДУ 2-го порядка Теорема: общее решение ур-я (1) есть сумма любого его частного реш-ия ỹ(x) и общего реш-ия соответствующего однородного ур-я Y(x), т.е. y=ỹ(x)+Y(x) (2) Док-во: пусть ỹ(x)-частное реш-ие соответствующего однородного ур-я ,где С1 и С2-произвольные постоянные. Покажем, что ф-ия (2) явл реш-ем ур-я (1).Для этого найдём y’=ỹ’(x)+Y’(x) Y’’=ỹ’’(x)+Y”(x) Подставим их в ур-ие (1): ỹ”(x)+Y”(x)+p(x)(ỹ’(x)+Y’(x))+q(x)(ỹ(x)+Y(x))=(ỹ”(x)+ỹ’(x)+ỹ(x))+(Y”(x)+Y’(x)+Y(x))=f(x)+0=0. Для того, чтобы убедиться, что это решения явл. Общим решением ур-я (1), остаётся показать, что из него можно выделить единственное частное решение, удовл. Нач. усл-ям: y(x0)=y0 и y’(x0)=y0’ (3) Пусть y1(x) и y2(x)- два частных решения ЛОДУ, образующих фундаментальную систему частных решений и y=ỹ(x)+C1y1(x)+C2y2(x) (4) Пусть y=ϕ(x) – какие-либо решения неоднородного ур-я (1), удовл-ее нач усл-ям (3). Покажем, что оно может быть выделено из решения (4) соответствующим набором постоянных С1 и С2. Дествительно, т.к. y’=ỹ’(x)+C1y1’(x)+C2y2’(x), то подставляя нач усл-я, получим систему ур-ий для определения неизвестных С1 и С2  Или 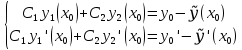 Эта система имеет ед-ное решение 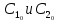 , т.к. её определитель есть вронскиан W(x0)≠0. Полученное частное решение , т.к. её определитель есть вронскиан W(x0)≠0. Полученное частное решение 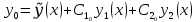 в силу теоремы о единственности совпадает с решением y=ϕ(x). Теорема доказана. в силу теоремы о единственности совпадает с решением y=ϕ(x). Теорема доказана. |
