Высш мат. Решение ду. Опред
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
36.Предельные теоремы в схеме Бернулли: Пуассона, Муавра-Лапласа. Теорема Пуассона. Пусть вероятность события А при каждом испытании в серии из n независимых испытаний равна 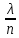 , где λ>0- постоянная, независящая от n, тогда вероятность Pn(m) при n→∞ и фиксированном m стремится к , где λ>0- постоянная, независящая от n, тогда вероятность Pn(m) при n→∞ и фиксированном m стремится к 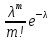 ( (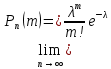 ) )m=(0;n), λ=np. Итак, если вероятность p события A мала, а число n независимых испытаний велико, можно пользоваться приближенной формулой: Pn(m) 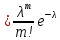 m=(0;n), λ=np. Локальная теорема Муавра-Лапласа. Пусть вероятность события А в n независимых испытаниях равна p, 0 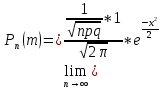 , где q=1-p, x= , где q=1-p, x=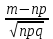 При больших n имеет место приближенная локальная формула Муавра-Лапласа: При больших n имеет место приближенная локальная формула Муавра-Лапласа: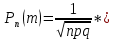 ϕ ϕ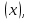 гдеϕ(x)= гдеϕ(x)=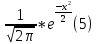 . .Функция ϕ 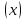 , определенная равенством (5) четная, т.е. ϕ(-x)=ϕ (x), поэтому в таблице приложений приведены ее значения только для x>0. , определенная равенством (5) четная, т.е. ϕ(-x)=ϕ (x), поэтому в таблице приложений приведены ее значения только для x>0.Интегральная теорема Муавра-Лапласа. Пусть m– число наступлений события А в серии из n независимых испытаний, p- вероятность наступления события А при каждом испытании, 0 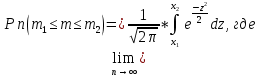 x1= x1=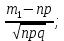 x2= x2=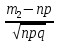 Другими словами при больших значениях n имеет место приближенная интегральная формула Муавра-Лапласа: 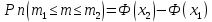 , где Ф(x)= , где Ф(x)=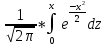 (7) (7)Функция (7) называется интегралом ошибок, она нечетная, т.е. Ф(-x)=-Ф(x). Ее значения при x≥0 приведены в таблицах приложений. 38. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях. Следствием из интегральной теоремы Муавра-Лапласа является формула для вычисления вероятности осуществления неравенства lm/n-pl 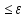 , , то есть вероятности того, что отклонение относительной частоты m/n наступления события А от его вероятности p не превышает по абсолютной величине некоторого заданного числа e: 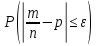 =2Ф =2Ф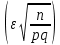 39. Дискретные СВ и з-ны их распределения Величина, которая может принимать только счётное или конечное множество значений называется дискретной. Значение ДСВ можно записать в виде конечной или бесконечной последовательности х1, х2,… хn Если для каждого хi (i = 1,2,3…) определить соотв-щую вероятность pi= P(X = xi), то мы получим яд распределения данной СВ X x1 x2 … xi … pp1 p2 … pn … Что бы эта таблица была законом распределения дожны выполнятся два требования : 1. рi ≥ 0 2. p1+ p2 +…+ pn +… = ∑ pn = 1 Существует два способа задания ДСВ х: с помощью функции распределения с помощью закона распределения (таблицы) 40. Непрерывные случайные величины и законы их распределения Непрерывной называется случайная величина которая может принимать все значения из некоторого конечного и бесконечного промежутка. Число возмоных НСВ бесконечно. Задание НСВ с помощью функции распределеня F(x) не является ед. способом задания. НСВ можно так же задать используя другую функцую, которую называют плотностью вероятностей.(Или дифф. Функция распределения) Определение: Плотностью вероятностей НСВ X или дифф. Ф-ия распределения – называют функцию F(x) – первую производную от фунции распределения F(x): f(x)=F’(x) 41. функция распределения вероятностей СВ и ее свойства. способом задания закона распределения вероятностей является и функция распределения. Функцией распределения св ( интегральная функция распределения) называется функция 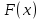 , которая для любого числа , которая для любого числа 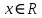 равна вероятности события равна вероятности события 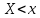 . .Свойства Функция ограничена 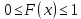 Функция не убывающая, т.е если 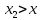 , то , то 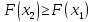 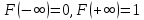 Вероятность попадания св Х в промежуток равна 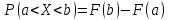 Функция непрерывна слева 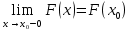 42. Дифференциальная функция распределения непрерывной СВ ( плотность распределения СВ), её свойства. Непрерывной называет случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Пример: продолжительность работы электролампы, дальность полета снаряда. Задание НСВ с помощью функции распределения F(x) не является единственным способом задания. НСВ можно также задать используя другую функцию, которую называют плотностью вероятностей или дифференциальной функцией распределения. Плотностью вероятностей НСВ называют функцию f(x)- первую производную от функции распределения F(x) : f(x)=F’(x) Заметим, что для описания распределения вероятностей ДСВ плотность распределения неприменима. Свойства плотностей вероятностей: Функция f(x)≥0 для любых xєR F(x) –неубывающая функция , следовательно f(x)=F’(x)≥0 Справедливо равенство P(a≤X≤b)= 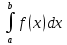 Действительно P(a≤X≤b)=F(b)-F(a)= 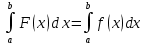 Если f(x)- плотность вероятностей СВ X , то F(x) = 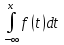 В самом деле так как F(-∞)=0, то F(x)=F(x)-F(-∞)= 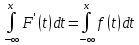 Имеет место соотношение 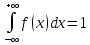 называемое условием нормировки называемое условием нормировкиДействительно 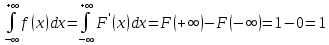 График плотности распределения называется кривой распределения. Отметим особенности, которые присущи любой кривой распределения: Она всегда лежит в верхней координатной полуплоскости Площадь, заключенная между этой кривой и осью Ox = 1. 44. Дисперсия случайной величины и её св-ва. Среднее квадратичное отклонение. Дисперсия СВ – это мат. ожидание квадрата отклонения СВ Х от её мат. ожидание и обознач. : D(X)= M(X- M(X))2. Если Х ДСВ, то D(X)= 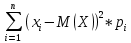 . .Если Х НСВ, с плотностью распределения f(x),то: D(X)= 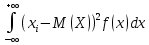 . .Если НСВ Х принимает значения на отрезке [a,b], то: D(X)= 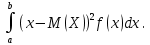 Среднее квадратичное отклонение: σ(x)= 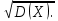 Св-ва: 1. Дисперсия постоянной величины всегда =0, D(C)=0. Дейс-но: D(C)= M(C-M(C))2= M(C-C)2=0. 2. Постоянный множитель выносится за знак дисперсии, возводится в квадрат: D(kX)=k2D(X). 3.Дисперсия алгебраической суммы 2-х неизвестных величин = сумме их дисперсии т.е.: D(X±Y)= D(X)+D(Y). 4. Упрощенное правило вычисл. дисперсии: D(X)= M(X)2- (M(X))2. 45. Биномиальное распределение и его численные характеристики Это один из основных законов распределения ДСВ. Пусть производится n независимых испытаний, в каждом из которых А может либо появится либо не появится. Вероятность наступления события во всех испытаниях постоянна и равна р, а не появления q = 1-p. Рассмотрим в качестве ДСВ Х – число появлений события А в этих испытаниях. Поставим задачу найти закон распределения величины Х. Для её решения требуется определить возможные значения Х и их вероятности. Очевидно, событие А в n испытаниях может либо не появится, либо появится один раз, либо 2 раза, либо 3 раза и т.д., либо n раз. Таким образом, возможные значения СВ Х таковы: х1=0, х2=1, х3=2 … хn+1=n. Остаётся найти вероятности этих возможных значений для чего достаточно воспользоваться формулой Бернулли: Pn(x) = Сnkpkqn-k(9), где k от 0 до n Формула 9 и является аналитическим выражением искомого закона распределения. Биномиальным называют распределение вероятностей определяемое формулой Бернулли. Закон назван биномиальным, т.к. правая часть равенства 9 можно рассматривать как общий член разложения Биномо-Ньютона: (p+q)n = Сnnpn+ Сnn-1pn-1q + … + Сnkpkqn-k + Сn0qn Таким образом, 1-ый член разложения pnопределяет вероятность наступления рассматриваемого события n раз в n независимых испытаниях; 2-ой член Сnn-1 = npn-1q определяет вероятность наступления рассматриваемого события n-1 раз; последний член qnопределяет вероятность того, что событие А не появится ни разу. Покажем биномиальный закон в виде таблицы
Теорема 1: математическое ожидание биномиального распределения с параметрами n и p равно произведению np, т.е. M(X) = np Теорема 2: дисперсия биномиального распределения с параметрами n и p равна произведению npq, т.е. D(X) = npq (σ = 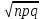 ) )46.Равномерное и показательное распределение, их числовые характеристики. Равномерное распределение: Непрерывная случайная величина, которая принимает значения на отрезке [a;b] с постоянной плотностью распределения- называется распределенной по равномерному закону. Из определения следует, что плотность распределения определяется равенством 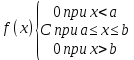 Должна удовлетворять двум требованиям f(x)≥ 0 , C>0 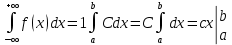 =C(b-a) =C(b-a)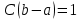 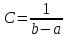 Таким образом: 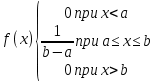 Найдем дисперсию и математическое ожидание и математическое отклонение : 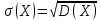 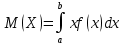 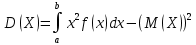 Показательное распределение: Непрерывная случ вел, которая принимает только не отрицательное значение с плотностью распределения 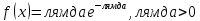 Называется распределением по показательному закону с параметром лямда, т к 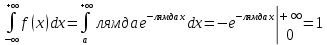 , то приведенное определение корректно. , то приведенное определение корректно.Ф-ция распределения показательного распределения имеет вид:  47.Нормальное распределение и его числовые характеристики . Нормальны называют распределение вероятностей непрерывной случайной величины (НСВ), которое описывается плотностью f(x)= 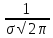 e- e-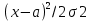 ,мы видим что нормальное распределение определяется двумя параметрами а и 𝜎 .Достаточно знать эти параметры чтобы задать нормальное распределение .Покажем что вероятностный смысл этих параметров таков :а -есть математическое ожидание ,𝜎 –среднее квадратическое отклонение нормального распределения . ,мы видим что нормальное распределение определяется двумя параметрами а и 𝜎 .Достаточно знать эти параметры чтобы задать нормальное распределение .Покажем что вероятностный смысл этих параметров таков :а -есть математическое ожидание ,𝜎 –среднее квадратическое отклонение нормального распределения .а) По опр. математического ожидания НСВ М(Х)= 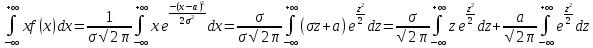 Первое слагаемое равно 0(под знаком интеграла стоит нечётная функция ,приделы интегрирования симметрично относительно начало координат ).Второе слагаемое равно а(интеграл Пуассона Первое слагаемое равно 0(под знаком интеграла стоит нечётная функция ,приделы интегрирования симметрично относительно начало координат ).Второе слагаемое равно а(интеграл Пуассона 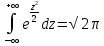 ) итак математическое ожидание М(Х)=0+а=а ,т.е математическое ожидание нормального распределения равно параметру а. ) итак математическое ожидание М(Х)=0+а=а ,т.е математическое ожидание нормального распределения равно параметру а.б)По опр. дисперсии НСВучитывая что М(Х)=а имеем D(X)= 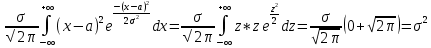 ;D(X)= ;D(X)=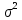 , ,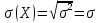 Среднее квадратичное отклонение нормального распределение равно параметру 𝜎. 49. Предмет и задачи математической статистики. Генеральная и выборочная совокупности. Статистическое распределение выборки. МС- это раздел прикладн. матем. непосредственно примыкающий к ТВ. Основное отличие МС от ТВ состоит в том, что в МС рассматриваются не действия законом распределения и числовым характер. СВ, а приближенные методы отыскания этих законов и характер по результатом эксперементов. Разработка методов регистрации, анализа, описания эксперемент. данных получаемых в результате наблюдения массовых случ. явлений составляет предмет математической статистики. Задачи, которые решаются с её помощью принимают ту или иную форму в зависимости от характера вопроса и объема накопленного опытного материала. Если при обработке экспериментального материала, з-н распределения СВ задача обработки результатов состоит в определении так наз. подходов значений или оценок для искомых параметров, т.е таких приближенных значений, которые при массовом применении приводили бы к меньшим погрешностям, чем всякие другие. С задачей отыскания подходящих значений числовых характер. тесно связана задача оценки их точности и надежности. Для решения подобных задач МС выработала ряд специальных приемов. В МС изучение СВ тесно связано с выполнением ряда независимых опытов в которых она принимает определенные значения. Полученные значения СВ представляют собой простую статистич. совокупность или простой статистический ряд, подлежащий обработке, осмыслению и научному анализу. Статистическая совокупность представляет собой множество объектов относительно некоторого качественного или количественного признака характериз. эти объекты Совокупн. состоящая из всех объектов, которые могут быть к ней отнесены наз. генеральной. Теоретически это б.б или приближ. к ∞ совокупность. Число объектов генеральн. совокупн. наз. её объемом и обознач: N Множество объектов случайно отобран. из генеральной совокупности наз. выборочной совокупностью или выборкой. Число объектов выборки наз. её объемом и обознач: n Юля того, что бы св-во выборки достаточно хорошо отражали св-ва генераль совокупн. выборка должна быть репрезентативной (представительной) Согласно з-ну больших чисел можно утверждать, что выборка будет репрезент. если её осуществляет случайно каждый объект, считается отобранной случайно из генеральной совокупн. если все объекты имеют одинаковую вероятность попасть в выборку. В зависимости от техники отбора объектов из генеральной совокупности выборки делятся на: повторные, бесповторные |
