Высш мат. Решение ду. Опред
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
11. ЛНДУ 2-го порядка со специальной правой частью Рассмотрим ЛНДУ 2-го порядка yʺ +pyʹ +qy = f(x)(1), где p и q – действительные числа, f(x) – непрерывная функция. Общее решение ЛНДУ y = ỹ(x) + Y(x), где ỹ(x) – частное решение неоднородного уравнения, а Y(x) – общее решение соответствующего однородного уравнения. Рассмотрим вопрос о нахождении ỹ(x). Рассмотрим различные виды правой части уравнения 1. f(x) = Pn(x) eax , где Pn(x) – многочлен степени n n = 0, то P0(x) = A n = 1, то P1(x) = Ax + B n = 2, то P2(x) = Ax2 + Bx + C если a не является корнем характеристического уравнения, то ỹ(x) = Qn(x) eax, где Qn(x) – многочлен степени n с неопределёнными коэффициентами б) если а является корнем характеристического уравнения, то ỹ(x) = xrQn(x) eax, где r – кратность корня характеристического уравнения (для ДУ 2-го порядка r = 1, либо r = 2) II. f(x) = eax (Pn(x) cos bx + Qm(x) sin bx) а) если (a+bi) – не является корнем характеристического уравнения то ỹ(x) = eax(Sn(x) cosbx + Tn(x) sinbx), где N = max {n, m} б) если (a-bi) – является корнем характеристического уравнения то ỹ(x) = xreax(Sn(x) cosbx + Tn(x) sinbx), где r – кратность корня характеристического уравнения. 12.Двойные интегралы, их свойства и вычисление в декартовых координатах. Двойным интегралом от ф-ции f(x;у) по области τ наз. Предел к которому стремится интегральная сумма 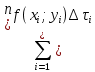 , при неограниченном увеличении числа n-малых площадок , при неограниченном увеличении числа n-малых площадок 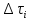 и при условии, что каждая из них стягивается в точку. Таким образом двойной ин-л: и при условии, что каждая из них стягивается в точку. Таким образом двойной ин-л: 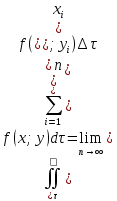 Св-ва:1)постоянный множитель можно выносить за знак ин-ла: 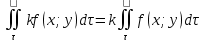 2)двойной ин-л от алгебраической суммы равен алг.сумме каждого слагаемого в отдельности. 2)двойной ин-л от алгебраической суммы равен алг.сумме каждого слагаемого в отдельности.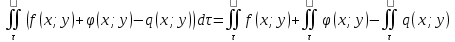 3)если в обл.интегрирования τ имеет место неравенство: f(x;y) ≥0, то 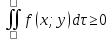 4)если в область интегрирования 4)если в область интегрирования  имеет место нер-во:f(x;y)≥q(x;y), то имеет место нер-во:f(x;y)≥q(x;y), то 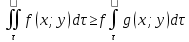 5) если обл. инт-ия τ разбита на 5) если обл. инт-ия τ разбита на 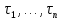 , то , то 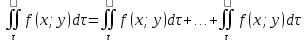 6)т-ма о среднем значении. Пусть ф-ция f(x;y) непрерывна в замкнутой ограниченой области τ, тогда в области τ сущ. точка укккккккккккккккккккккк 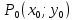 такая, что такая, что 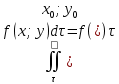 . (1) Значение ф-ций f( . (1) Значение ф-ций f(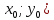 опред. из равенства (1) наз. cредним значением функции f(x;y) в области τ. опред. из равенства (1) наз. cредним значением функции f(x;y) в области τ. Вычисление в декартовых координатах. Т-ма: Пусть ф-ция f(x;y) задана и непрерывна в замкнутой прямоугольной D,тогда имеет место неравенство: 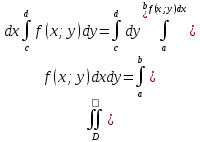 Пусть любая прямая параллельна оси Оу пересекает границу обл. D не более, чем в 2ух точках, тогда справедлива Пусть любая прямая параллельна оси Оу пересекает границу обл. D не более, чем в 2ух точках, тогда справедлива ф-ла: 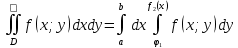 Рассмотрим обл.D, которая определяется неравенствами:с≤y≤d, 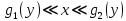 и пусть любая прямая параллельна оси Ох пересекает границу области не более, чем в 2х точках, тогда двойной интеграл: и пусть любая прямая параллельна оси Ох пересекает границу области не более, чем в 2х точках, тогда двойной интеграл: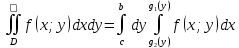 13.Тройные интергалы, их св-ва и вычисление в декартовых системах. Тройной интеграл 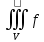 (x;y;z)*dx*dy*dz= (x;y;z)*dx*dy*dz= ( ( ; ;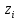 ) )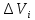 = =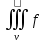 (x;y;z)dv (1). (x;y;z)dv (1).dv= dx*dy*dz –элемент объема. Теорема(существования). Если функция u=f(x;y;z) неопределенна в ограниченной замкнуто области V,то предел интегралной суммы (1) при n→∞ и max 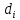 →0 существует и не зависит ни от способа разбиения области V на части, ни от выбора точек →0 существует и не зависит ни от способа разбиения области V на части, ни от выбора точек 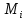 ( (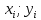 ; ;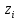 ) в них. ) в них.Свойства: 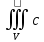 * f(x;y;z)dv=c * * f(x;y;z)dv=c * 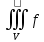 (x;y;z)dv, c-const. (x;y;z)dv, c-const.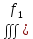 (x;y;z) (x;y;z)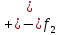 (x;y;z))dv= (x;y;z))dv=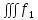 (x;y;z) (x;y;z)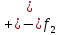 (x;y;z))dv (x;y;z))dv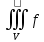 (x;y;z)dv= (x;y;z)dv=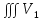 f(x;y;z)dv+ f(x;y;z)dv+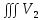 f(x;y;z)dv f(x;y;z)dv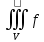 (x;y;z)dv≥0если в области V функция f(x;y;z)≥0. (x;y;z)dv≥0если в области V функция f(x;y;z)≥0.Если в области интегрирования f(x;y;z)≥φ (x;y;z) то и 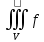 (x;y;z)dv≥ (x;y;z)dv≥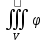 (x;y;z)dv. (x;y;z)dv.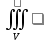 dv= V т.к. в случае f(x;y;z)=1 любая интегральная сумма имеет вид dv= V т.к. в случае f(x;y;z)=1 любая интегральная сумма имеет вид 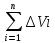 =V и численно равна объему тела. =V и численно равна объему тела.Оценка тройного интеграла: m*V=≤ 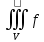 (x;y;z)dv≤M*V, где m,M соответственно наим. и наиб. Значения функции f(x;y;z) в области V. (x;y;z)dv≤M*V, где m,M соответственно наим. и наиб. Значения функции f(x;y;z) в области V.7.Теорема о среднем: 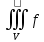 (x;y;z)dv=f( (x;y;z)dv=f(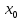 , ,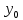 , ,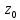 )*V, где V –объем тела. )*V, где V –объем тела.Тройной интеграл вычисляется в декартовых системах с помощью формулы: 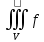 (x;y;z)dxdydz= (x;y;z)dxdydz=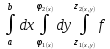 (x;y;z)dz (x;y;z)dz14. Приложения двойных и тройных интегралов ДВОЙНОЙ ИНТЕГРАЛ -Объём цилиндрического тела: 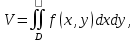 где 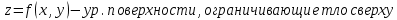 . .-Площадь плоской фигуры области D: 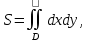 -Масса плоской фигуры: 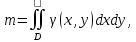 Где 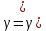 x,y)- переменная плотности. x,y)- переменная плотности.ТРОЙНОЙ ИНТЕГРАЛ -Объём тела: Объём обл. 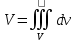 или или 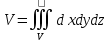 - в дек. Координатах - в дек. Координатах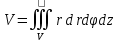 - в цилиндрических координатах - в цилиндрических координатах - в сферических координатах - в сферических координатах-Масса тела: 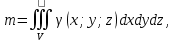 где γ(x,y,z)- объёмная плотность распред. Массы в т. М(х,y,z). где γ(x,y,z)- объёмная плотность распред. Массы в т. М(х,y,z).15. Криволинейный интеграл первого рода его свойства, вычисление, применение На плоскости Оху задана непрерывная кривая АВ, определяющаяся функцией f(x;y). Разобьем кривую на точки 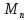 . Выберем на каждой дуге произвольную точку ( . Выберем на каждой дуге произвольную точку (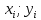 )и составим сумму )и составим сумму 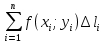 - интегральная сумма для данной функции по кривой АВ - интегральная сумма для данной функции по кривой АВКонечный предел интегральных сумм называют криволинейным интегралом от функции по кривой АВ (первого рода) 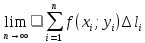 = =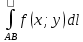 Теорема если функция непрерывна в каждой точке кривой, то криволинейный интеграл существует свойства 1 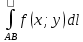 = = 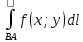 2 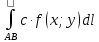 = = 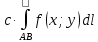 3 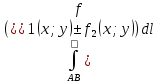 = = 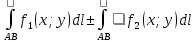 4 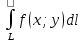 = = 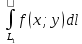 + + 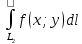 5 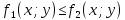 , , 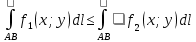 6 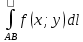 = = 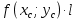 Вычисление Параметрическое 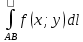 = =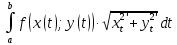 Явное 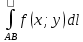 = = 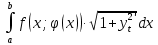 Полярное 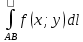 = =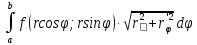 Применение Вычисление длины кривой, площади цилиндрической поверхности и массы кривой 17.Формула Остроградского-Грина Связь между двойным интегралом по области D и криволинейным интегралом по границе L этой области устанавливает формула Остроградского Грина, которая широко при меняется в математическом анализе. Теорема: Если функции Р(х; у) и Q(x; у) непрерывны вместе со своими частными производными dP/dy и dQ/dx в области D, то имеет место формула : ∫∫((dQ/dx)-(dP/dy))dxdy=∫Pdx+Qdy 19.Необходимый признак сходимости. Гармонический ряд 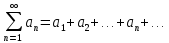 (1) – числовой ряд. (1) – числовой ряд.ТЕОРЕМА. Если ряд (1) сходится, то его общий член 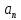 стремится к нулю, т.е. стремится к нулю, т.е. 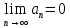 . (2) . (2) Доказательство. Пусть дан сходящийся ряд 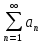 , имеющий сумму S. Рассмотрим его частичные суммы , имеющий сумму S. Рассмотрим его частичные суммы 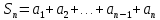 ; ; 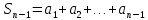 . Отсюда . Отсюда 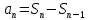 . Следовательно, . Следовательно,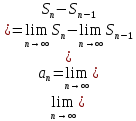 . .Но 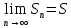 и и 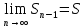 , т.е. при , т.е. при 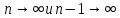 . .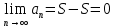 . Теорема доказана. . Теорема доказана.СЛЕДСТВИЕ. ( Достаточное условие расходимости ряда) Если 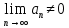 или не существует, то ряд расходится. или не существует, то ряд расходится.Условие (2) является необходимым для сходимости ряда (1), но недостаточное. Это означает, что существуют расходящиеся ряды, для которых выполняется условие (2). Примером может служить ряд 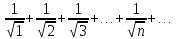 (3). (3). 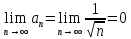 , однако ряд расходится. , однако ряд расходится.Рассмотрим так называемый гармонический ряд: 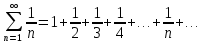 (4) (4) Как известно, 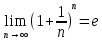 . Отсюда следует, что при любом . Отсюда следует, что при любом  имеет место неравенство имеет место неравенство 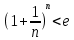 . Логарифмируя это неравенство по основанию . Логарифмируя это неравенство по основанию 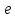 , получим: , получим: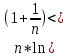 1, 1,т.е. 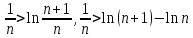 Подставляя в полученное нерав-во поочередно  , получим: , получим: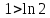 , ,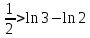 , ,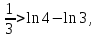 ………….. 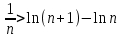 Сложив почленно эти неравенства, получим 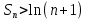 . Поскольку . Поскольку 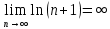 , получаем , получаем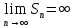 , т.е. гармонический ряд (4) расходится. , т.е. гармонический ряд (4) расходится. 20.Достаточные признаки сходимости знакопостоянных рядов Признак сравнения пусть даны два ряда 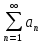 (1) и (1) и 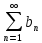 (2). Eсли выполняется неравенство (2). Eсли выполняется неравенство 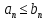 , то: , то:если ряд 2 сходится, то и ряд 1 сходится; если ряд 1 расходится, то и ряд 2 расходится. Предельный признак сравнения Если существует предел 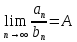 отличный от нуля, то ряды сходятся или расходятся одновременно. отличный от нуля, то ряды сходятся или расходятся одновременно.Признак Даламбера если существует предел 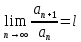 , то при L<1 ряд сходится, приL>1 – расходится. , то при L<1 ряд сходится, приL>1 – расходится.Радикальный признак Коши Если существует предел 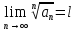 , то при L<1 ряд сходится, приL>1 – расходится. , то при L<1 ряд сходится, приL>1 – расходится.Интегральный признак Коши Если члены ряда могут быть представлены как значения монотонно убывающей функции, то: если 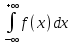 сходится, то и ряд сходится; сходится, то и ряд сходится;если 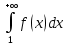 расходится, то и ряд расходится. расходится, то и ряд расходится.22. Знакочередующиеся РЯДЫ. Признак Лейбница Знакочередующимся рядом называется ряд вида a1-a2+a3-a4+…+(-1)n+1an+…=∑(-1)n+1an (1) где n > 0 для всех n принадлежащих N Для знакочередующихся рядов имеет место достаточный признак сходимости. Теорема.1 (признак Лейбница). 3накочередующийся ряд (1) сходится, если: 1. Последовательность абсолютных величин членов ряда монотонно убывает, т. е. аl > а2 > аЗ > ... > аn> ... ; 2. Общий член ряда стремится к нулю: Iim an = 0. При этом сумма S ряда (1) не превосходит первого члена а1, а остаток ряда удолетворяет неравенству 0 Док: рассм сначала частичную сумму четного числа(2m) членов ряда(1) S=u1-(u2-u3)-(u4-u5)-…-(u2m-2 -u2m-1)-u2m. Легко видеть, что S2m Рассм. теперь частичные суммы нечетного числа (2m+1) членов ряда (1). Очевидно, что S2m+1=s2m+u2m+1. Отсюда следует, что limS2m+1= limS2m+o=S. Итак, limSn=S как при четном ,так и при нечетном n. Следовательно, ряд (1) сходится. |
