Высш мат. Решение ду. Опред
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
49.Если выборки отбирают по одному элементу, который обследуют и снова возвращают в генеральн. совокупн., то выборка наз повторной. Если объекты выборки не возращ. в генеральн. совокупн., то выборка наз. бесповторной. На практике обычно пользуются бесповторной выборкой. При больших объемах N генеральн. совокупности и малом относительном объеме n выборки, различия в формулах описывающих обе выборки по технике их отбора не велики. Как правило результаты, эксперемен. наблюдения дискретн. СВ, сводятся в таблицу , в первой строке которой записывается номер i-эксперем., а во второй—соответственно наблюдения. Хi-назыв. вариантой СВ Х, такие таблица наз. статистическими рядами несгрупированных данных. Статистич. Ряд расположен по возрастанию варианта наз. вариационным. Пусть miчастота наблюдения варианта хi n= 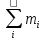 - общее число наблюдений, т.е объем выборки. - общее число наблюдений, т.е объем выборки.Величина Wi= 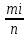 — наз. относительной частотой наблюдения. Таблица совокупных данных по частоте и относительной частоте наблюдений наз. статистическим рядом сгруппированных данных. — наз. относительной частотой наблюдения. Таблица совокупных данных по частоте и относительной частоте наблюдений наз. статистическим рядом сгруппированных данных.Статический ряд распределения МС явл. аналагом ряда распределения СВ Х ТВ. В случае, когда n велико или СВ Х явл. Непрерывной составляющей интервальный статистический ряд. Для этого в первую строку табл. статист. распред. вписывают частные промежутки [x0, x1), [x1, x2), [x2, x3),…, [xn, xn+1]. Которые как правило берутся одинаковые по длине—шаг разбиения n=x1-x0=x2-x1=x3-x2… Выбор количества интервалов существенно зависит от объема выборки. В литературе приводятся рекомендации по выбору числа интегралов, однако они существенно отличаются одна от другой.Рекомендуют использовать теорему Стерджеса, согласно его формуле рекомендуемое число интервалов разбиения k≈1+3.322lgn, а длины частных интервалов 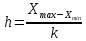 предполагая, что весь интервал имеет вид [xmin,xmax]. За начало первого интервала рекомендуется брать хнач=xmin-h/2. Во вторую строку таблицы записывают количество результатов наблюдения mi(i=͞1,͞k), попавших в каждый интервал. предполагая, что весь интервал имеет вид [xmin,xmax]. За начало первого интервала рекомендуется брать хнач=xmin-h/2. Во вторую строку таблицы записывают количество результатов наблюдения mi(i=͞1,͞k), попавших в каждый интервал.50.Полигон и гистограмма. Эмпирическая функция распределения и ее свойства. Статистические ряды сгруппированных данных представляет график и диограмму наиболее распространенными из которых являются полигон и гистограмма Полигоном частот называют ломаную, отрезки которой соединяют точки (х1; n1), (x2; n2), …, (xk; nk). Для построения полигона частот на оси абсцисс откладывают варианты xi, a на оси ординат—соответствующие им частоты ni. Точки (xi ;ni) соединяют отрезками прямых и получают полигон частот. Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (х1; W1), (х2W2), …..., (xk; Wk). Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, a высоты равны отношению ni/h (плотность частоты).Пусть известно статистическое распределение частот количественного признака X. Обозначим через число наблюдений, при которых наблюдалось значение признака, меньшее x и через n – общее число наблюдений. Очевидно, относительная частота события X 2.F*(x)— неубывающая функция. 3.Если x1 – наименьшая варианта, то F*(x)=0 при ,если xk – наибольшая варианта, то F*(x)=1 при . Эмпирическая функция распределения F*(x) служит для оценки теоретической функции распределения генеральной совокупности 51.Числовыехарактеристики вариационного ряда. Точечные оценки параметров распределения по опытным данным. Одной из основных числовых характеристик вариационных рядов является средняя арифметическая. Данная величина показывает центральное значение признака, вокруг которого сосредоточенны все наблюдения. Средней арифметической вариационного ряда называется сумма произведений признаков (вариантов) ряда на соответствующие им частости. 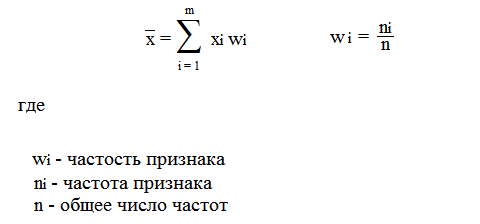 Средним линейным отклонением вариационного ряда называется средняя арифметическая модуля отклонения признаковот их средней арифметической. 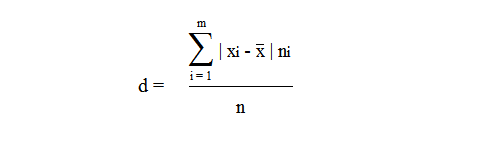 Дисперсией s2 вариационного ряда называется средняя арифметическая квадратов отклонений признаков от их средней арифметической. 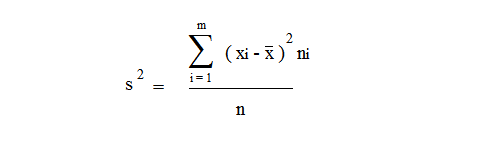 Среднее квадратическое отклонение вариационного ряда равно квадратному корню из дисперсии. 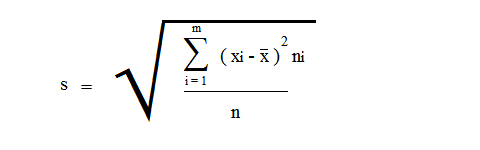 51.Важным показателем вариационного ряда является также коэффициент вариации, который показывает однородность исследуемого признака.  Точечные оценки могут быть состоятельными, несмещенными и эффективными. Состоятельной называется оценка, которая при увеличении объема выборки стремится по вероятности к истинному значению числовой характеристики. Несмещенной называется оценка, математическое ожидание которой равно оцениваемой числовой характеристике (параметру). Оценка называется эффективной, если ее дисперсия меньше дисперсии любой другой оценки данного параметра, т.е. наиболее эффективной считают ту из нескольких возможных несмещенных оценок, которая имеет наименьшую дисперсию. 52.Интервальная оценка параметров распределения по опытным данным . Понятие доверительного интервала и доверительной вероятности. Все выборочные характеристики являются случайными величинами.Это означает, что для другой выборки того же объема значения выборочных характеристик получатся другими. Таким образом, выборочныехарактеристики являются лишь оценкамисоответствующих характеристик генеральной совокупности. Недостатки выборочного оценивания компенсируетинтервальная оценка,представляющая числовой интервал,внутри которого с заданной вероятностью Рднаходится истинное значение оцениваемого параметра. Пусть Ur - некоторый параметр генеральной совокупности (генеральное среднее, генеральная дисперсия и т.д.). Интервальной оценкойпараметра Ur называется интервал (U1, U2),удовлетворяющий условию: P(U < Ur < U2) = Рд Вероятность Рдназывается доверительной вероятностью. Доверительная вероятностьРд-вероятность того, что истинное значение оцениваемой величины находится внутриуказанного интервала. При этом интервал (U1, U2)называется доверительным интерваломдля оцениваемого параметра. Длина доверительного интервала, характеризующая точность интервальной оценки, зависит от объема выборки п и надежности γ (уровня значимости γ= 1 - α). При увеличении величины п длина доверительного интервала уменьшается, а с приближением надежности γ к единице — увеличивается. Выбор α (или γ = 1 - α) определяется конкретными условиями. Обычно используется α=0,1; 0,05; 0,01, что соответствует 90, 95, 99%-м доверительным интервалам. 53. Доверительный интервал для неизвестного математического ожидания нормально распределенной СВ при известной дисперсии . Пусть случайная величина имеет нормальное распределение: Примем без доказательства, что если случайная величина распределена нормально, то и выборочное среднее , найденное по независимым наблюдениям, также распределено нормально.Параметры распределения таковы: 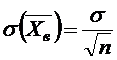 . .Из теории вероятности известна формула для нормально распределенной случайной величины : 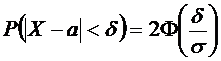 ,где ,где 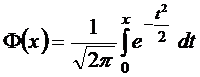 - функция Лапласа, значение которой в точке находим по таблице .Учитывая, что имеет нормальное распределение можно записать - функция Лапласа, значение которой в точке находим по таблице .Учитывая, что имеет нормальное распределение можно записать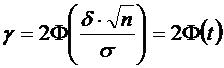 ,где ,где 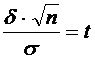 Из последнего равенства по таблице Лапласа находим Тогда и доверительный интервал 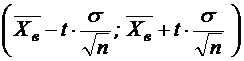 покрывает с надежностью математическое ожидание покрывает с надежностью математическое ожидание 54.Статистическая проверка гипотез. Критерий согласия Пирсона Если з-н распределения неизвестен, но есть основания предполагать, что он имеет определенный вид (назавём его А), то проверяют нулевую гипотезу: генеральная совокупность распределена по закону А. Проверка гипотезы о предполагаемом законе неизвестного распределения производится при помощи специально подобранной СВ-критерий согласия. Критерием согласия— наз. критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Критерий согласия Пирсона (χ2) применяют для проверки гипотезы о соответствии эмпирического распределенияпредполагаемому теоретическому распределению F(x) при большом объеме выборки (n ≥ 100). Критерий применим для любых видов функции F(x), даже при неизвестных значениях их параметров, что обычно имеет место при анализе результатов механических испытаний. В этом заключается его универсальность. Использование критерия χ2 предусматривает разбиение размаха варьирования выборки на интервалы и определения числа наблюдений (частоты) nj для каждого из e интервалов. Для удобства оценок параметров распределения интервалы выбирают одинаковой длины. Число интервалов зависит от объема выборки. Обычно принимают: при n = 100 e = 10 ÷ 15, при n = 200 e = 15 ÷ 20, при n = 400 e = 25 ÷ 30, при n = 1000 e = 35 ÷ 40. Интервалы, содержащие менее пяти наблюдений, объединяют с соседними. Однако, если число таких интервалов составляет менее 20 % от их общего количества, допускаются интервалысчастотой nj≥2. Статистикой критерия Пирсона служит величина 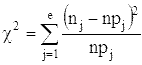 , (1) , (1)где pj - вероятность попадания изучаемой случайной величины в j-и 54.интервал, вычисляемая в соответствии с гипотетическим законом распределением F(x). При вычислении вероятности pj нужно иметь в виду, что левая граница первого интервала и правая последнего должны совпадать с границами области возможных значений случайной величины. Например, при нормальном распределении первый интервал простирается до -∞, а последний - до +∞. Нулевую гипотезу о соответствии выборочного распределения теоретическому закону F(x) проверяют путем сравнения вычисленной по формуле (1) величины с критическим значением χ2α, найденным по табл. VI приложения для уровня значимости α и числа степеней свободы k = e1 - m - 1. Здесь e1 - число интервалов после объединения; m - число параметров, оцениваемых по рассматриваемой выборке. Если выполняется неравенство χ2 ≤ χ2α (2) то нулевую гипотезу не отвергают. При несоблюдении указанного неравенства принимают альтернативную гипотезу о принадлежности выборки неизвестному распределению. Недостатком критерия согласия Пирсона является потеря части первоначальной информации, связанная с необходимостью группировки результатов наблюдений в интервалы и объединения отдельных интервалов с малым числом наблюдений. В связи с этим рекомендуется дополнять проверку соответствия распределений по критерию χ2 другими критериями. Особенно это необходимо при сравнительно малом объеме выборки (n ≈ 100). 7. линейные однородные дифференциальные уравнения второго порядка, свойства их решения Определение 1. Дифференциальное уравнение n – го порядка называется линейным, если оно является уравнением первой степени относительно совокупности искомой функции у и её производных где В дальнейшем мы будем предполагать, что функции Если и называется линейным однородным. Левая часть этого уравнения является однородной функцией первой степени относительно Основные свойства линейных однородных уравнений. Теорема 1. Если y1 и y2 – два частных решения линейного однородного уравнения второго порядка то y1 + y2 есть также решение этого уравнения. Теорема 2. если y1 есть решение уравнения (3) и С – постоянная, то Су1 есть также решение уравнения (3) Определение 2. Два решения уравнения (3) y1 и y2 называются линейно независимыми на отрезке Иными словами, два решения y1 и y2 называются называются линейно независимыми на отрезке |
