Высш мат. Решение ду. Опред
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
23. Знакопеременные ряды. Абсолютная и условная сходимость. Рассмотрим ряды с членами произвольных знаков такие ряды назыв знакопеременными . Возьмем знакоперем. Ряд а1+а2+…+аn…(1), где члены ряда могут быть разных знаков. Одновременно рассм. ряд, составленный из абсолютных величин ряда (1): Iа1I+Iа2I+…+IаnI…(2) Теорема: еслі ряд (2)сходится, то сходится и ряд (1) Признак является достаточным, но не обходимым . Все сходящиеся ряды делятся на абсолютно сход. и условно сход. К абсолютно сход. рядам относятся сход. ряды для которых ряды составленные из абсолютных велечин ихчленов так же сходятся, к условно сход . дядам относятся сход. ряды для которых ряды сост. из абсолютных велечин их членов расходятся. 24. Степенные ряды .Радиус и интервал сходимости.Теорема Абеля Опр.:ряд вида с0+c1x+c2x2+…+сnxn+…=∑cnxn (1) или вида : с0+c1(x-x0)+c2(x-x0 )2+…+сn (x-x0 )n+…=∑cn(x-x0)n (2) членами которого являются степенные функции наз-ся степенными .Действительные числа сn принадлежит R наз-ся коэффициентами степенного ряда .Степенной ряд (1) всегда сх-ся по крайней мере в точке х=0 ,а ряд (2)- в точке х=х0 Ряд (1) наз-ся рядом по степеням х ,а ряд (2) –по степеням х-х0 Т-ма Абеля:пусть степенной ряд (1) сх-ся в точке х0 не рано 0 ,тогда сх-ся абсолютно в любой точке х ,удовлетворяющей нер-ву │х│<│х0│и сх-ся равномерно в области │х│≤q<│х0│.Если же ряд расходится в некоторой точке х1,то он расходится во всех точках х таких что: │х│>│х1│.Теорема Абеля геометрически утверждает ,если х0-точка сх-ти,то на (-│х0│;│х0│) ряд сх-ся абсолютно,а если х1 точк расходимости ,то во всех точках вне интервала (-│х1│;│х1│) ряд расходится .Отсюда вытекает след.теорема: Т-ма:Если ряд (1) сх-ся не при всех значениях х ,то сущ-т R>0,что ряд абсолютно сх-ся при │х│ (-R;R)- интервал сх-ти степенного ряда R-радиус сх-ти степенного ряда R=lim│cn/cn+1│(получена в предположении существования конечного предела,т.е. ряд(1) содержит все степени х ),если к ряду (1 ) применить признак Коши,то получим:R=1/limкорень нной степени из cn 25. Функциональные ряды.Основные понятия.Область сходимости Опр.: функциональным рядом называется ряд вида:u1(x)+u2(x)+…+un(x)+…=∑un(x)(n от 1 до n)(1),где un(x)-функции определенные в некоторой области изменения аргумента .Придавая х определенное значение хо, мы получим числовой ряд u1(x0) + u2(x0) +…+ un(x0) +…, который может быть как сходящимся, так и расходящимся.Если полученный числовой ряд сходится, то точка хо называется точкой сходимости ряда (1); если же при х=х0 ряд расходится ,то х0- точкой pacxoдuмocти функционального ряда. Опр.: Совокупность всех точек сходимости функционального ряда называется областью его сходимости. Частичная сумма функц.ряда обозначается Sn(x): Sn(x)=ul (х) + u2(x) + ... + un(x) называется функцией переменной х limSn(x)=S(x),где S(x)-сумма ряда S(x)= ul (х) + u2(x) + ... + un(x)+… Если ф-ный ряд сх-ся и имеет сумму S(x),то разность S(x)-Sn(x) называется его n-ым остатком и обозначается rn(x): S(x)-Sn(x)= rn(x) ,lim rn(x)=0 rn(x)=un+1(x)+un+2(x)+… 26 Формула и ряд Тейлора,Маклорена Для люб ф-ции f(x) определенной в окрестн точки x0 и имеющей в ней производные до(n+1)-го порядка включит, справедлива формула Тейлора: f(x)=f(x0)+ 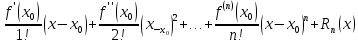 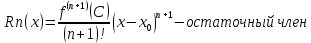 , где , где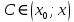 Если функция имеет производные любых порядков в окр-ти точки x0 и остаточный член ряда стремится к 0 при 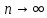 , получается разложение ф-ции по степеням , получается разложение ф-ции по степеням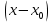 в ряд Тейлора: в ряд Тейлора:f(x)=f(x0)+ 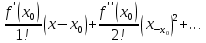 = =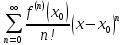 Ряд Тейлора сход к f(x) в точке х, если в этой точке остаточный член стремился к 0 т. е. 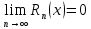 Если модули всех производных ф-ции f(x) ограничены в окрестности т-ки х0 одним и тем же числом М>0, то имеет место разложение в ряд Тей Если в ряде Тейл положить х0=0, то получ разложение ф-ции по степеням х в ряд Маклорена: f(x)=f(0)+ 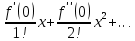 = =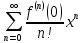 28. Элементы комбинаторики Комбинаторика – это раздел статистики в котором изучаются сколько комбинаций определенного типа можно составить из данных элементов. Перестановками наз. комбинации, состоящие из одних и тех же n-различных элементов и отличающихся только порядком. Pn=n! Размещениями наз. комбинации, состоящие из n-различных элементов по m-элементов, которые отличаются либо составом элементов, либо их порядком. 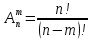 Сочетаниями наз. комбинации состоящие из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. 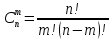 29. Основные понятия теории вероятностей Теория вероятностей – математическая наука, изучающая закономерности в случайных явлениях. Теория вероятностей изучает свойства массовых случайных событий, способных многократно повторяться при воспроизведении определенного комплекса условий. Основное свойство любого случайного события независимо от его природы - вероятность его осуществления. Одним из основных понятий теории вероятностей является оnыт. Подоnытом понимается выполнение комплекса условий, в результате которого происходят или не происходят определенные события (факты). Всякий результат опыта или наблюдения наз. событием. Событие наз. случайным, если в результате опыта оно может произойти, а может и не произойти. Событие наз. достоверным, если оно обязательно произойдет в условиях данного опыта. Невозможным наз. событие, которое в условиях данного опыта не может произойти. События, которые невозможно разложит на более простые наз. элементарными. Все остальные наз. составными или разложимыми. События наз. несовместными, если появление одного из них исключает появление другого события в условиях данного опыта. События наз. совместными, если появление одного из них не исключает появление другого в одном и том же опыте. Событие, которое состоит в не наступлении события А наз. противоположным. Несколько событий в условиях данного опыта обр. полную группу, если в результате опыта обязательно произойдет хотя бы одно из них. 30. Пространство элементарных событий. Алгебра событий. Одним из основных понятий теории вероятностей является оnыт. Подоnытом понимается выполнение комплекса условий, в результате которого происходят или не происходят определенные события. Простейшие неразложимые результаты опыта называются элементарными событиями, а вся совокупность элементарных событий называется nространством элементарных событий Ω={ωi}. С каждым опытом связано свое пространство элементарных событий Ω. Любое конечное или счетное подмножество Ω, называется событием. Различают три типа событий: 1) достоверные, которые всегда произойдут в результате опыта (Ω); 2) случайные, могут либо произойти в результате опыта, либо нет; 3) невозможные, никогда не произойдут в результате опыта (0 или ). События обычно обозначают первыми прописными буквами латинского алфавита: A, В, С,.... События A и В несовместны, если в результате одного опыта они не могут происходить одновременно, в противном случае - совместны. Например, при одном подбрасывании монеты не могут одновременно появиться герб и решка. Элементы последовательности событий A1, A2,..., An nоnарнонесовместны, если любые два из них несовместны. Например, при подбрасывании игральной кости никакие два элементарные исхода (появление цифр 1, 2, 3, 4, 5, 6) не могут произойти одновременно. Несколько событий равновозможны, если ни одно из них не имеет объективного преимущества перед другими. Например, элементарные исходы при подбрасывании монеты, игральной кости.События А1, A2,..., An образуют nолную груnnу, если в результате опыта кроме этих событий ничего не может произойти.Приведем примеры полных групп событий:- выигрыш и проигрыш в лотерее для одного лица;- выпадение «герба» и «цифры» при бросании одной монеты;- появление четной или нечетной цифры в том же опыте.Обычно Ω изображают на плоскости в виде некоторой области, а ωi в виде точек этой области, устанавливая, таким образом, соответствие между событиями и точечными множествами. Между событиями могут существовать некоторые соотношения. Если из того, что произойдет событие А, следует, что произойдет событие В, то говорят, что А влечет за собой В и обозн. так: АʗВ или ВכА.Событие, состоящее в том, что произойдет хотя бы одно из двух А и В (безразлично какое именно или оба если это возможно) наз. суммой двух событий и обозн. А+В.Событие, состоящее в одновременном наступлении события А и В наз. произведением этих событий и обозн. АВ. 31. Классическое и статистическое определение вероятности события Опр. Классической вероятностью Р(А) события А наз. отношение числа mэлементарных исходов благоприятствующих событию А к числу n всех элементарных исходов, т.е. Р(А) =  . .Из классического опред. следует её свойства: Вероятность достоверного события равна 1. Вероятность невозможного события равна 0 Вероятность произвольного события удовлетворяет 0<=P(A)=>1 Опр. Статистической вероятностью события А наз. число, характеризующее частоту события прибольшом числе испытаний, т.е. число около которого частота события колеблется, т.е. Р(А) =  32. Теорема сложения вероятностей. Теорема (сложение вероятностей несовместных событий): вероятность появления одного из двух несовместных событий равна сумме их вероятностей: Р(А+В) = Р(А)+Р(В). Доказательство. Введем обозн. м1 – число исходов благоприятствующих событию А, м2 – благоприят. событию В; n – общее число возможных элементарных исходов испытания. Следовательно, вероятность суммы Р(А+В) =  и тогда разделив, получим: Р(А+В) = и тогда разделив, получим: Р(А+В) =  , но Р(А)= , но Р(А)=  , P(A) = , P(A) =  из этого следует, что Р(А+В) = Р(А)+Р(В). из этого следует, что Р(А+В) = Р(А)+Р(В).Теорема 1. Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице. Доказательство. Т.к. появление 1-ого из событий полной группы достоверного события равна 1, то Р(А1+А2+…+Аn)=1. любые два события полной группы несовместны и можно применить теорему сложения Р(А1+А2+..+Аn) = Р(А1)+Р(A2)+…+P(An). Сравнивая эти формулы, получаем Р(А1+А2+…+Аn)=1. Доказано.  Теорема 2. Сумма противоположных событий равна единице, то есть P(A) + P(Ȧ) = 1 Доказательство. Противоположные события обр. полную группу событий, а сумма вероятностей таких событий равна 1. Доказано. Теорема (сложение вероятностей совместных событий). Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: Р(А+В) = Р(А) + Р(В) – Р(АВ) Доказательство. Поскольку события А и В, по условию, совместны, то событие А + В наступит, если наступит одно из следующих трех несовместных событий: AḂ, ȦB, AB. По теореме сложения вероятностей несовместных событий, имеем: Р(А + В) = Р(А ) + Р( В) + Р(АВ). Событие А произойдет, если наступит одно из двух несовместных событий: А или АВ. По теореме сложения вероятностей несовместных событий имеем: Р(А) = Р(А ) + Р(АВ). Отсюда, Р(А )=Р(А) – Р(АВ). Аналогично имеем, Р(В) = Р(ĀВ) + Р(АВ). Отсюда, Р(ĀВ) = Р(В) – Р(АВ). Подставляя в начальное равенство, получаем,Р(А + В) = Р(А) + Р(В) – Р(АВ). Что и требовалось доказать. 33. Условная вероятность(УВ). Теоремы умножения вероятностей. В ряде случаев приходится рассматривать в-ти событий при доп. условии, что произошло некоторой другое событие, имеющее в-ть, отличную от нуля. Такие в-ти наз. условными в-тями. В-ть события В при условии, что произошло событие А, наз-ся условной в-тью события В и обознач-ся так РА(В). Условная вероятность по определению равна: РА(В) =  , (Р(А) >0). , (Р(А) >0).Теорема (умножение вероятностей зависимых событий): Вероятность произведения двух событий равна произв-нию вер-ти одного из них на условную в-ть другого при условии, что первое событье произошло. P(AB) = P(A)*PA(B). Доказательство. По определению условной вероятности РА(В) =  , отсюда Р(АВ)=Р(А)*РА(В), что и требовалось доказать. , отсюда Р(АВ)=Р(А)*РА(В), что и требовалось доказать. Замечание: Применив последнюю формулу к событию ВА, получаем Р(ВА)=Р(В)*РВ(А), но Р(ВА) = Р(АВ) Следствие: Вероятность совместного появления нескольких событий равна произведению одного из них на условные вероятности всех. Причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились. Опр. Событие В наз. независимым от события А, если появление событие А не изменяет вероятности появления события В, т. е. если условная вероятность события В равна его безусловной вероятности: РА(В) = Р(В) Теорема(умножение вероятностей независимых событий): вероятность совместного появления 2-ух независимых событий равна произведению вероятностей этих событий: Р(АВ)=Р(А)*Р(В). 34. Формула полной вероятности. Формула Байеса. Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий В1, В2,…,Вn, образующих полную группу равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события: Р(А) = Р(В1)*РВ1(А) + Р(В2)*РВ2(А) + … + Р(Bn)*РВn(A) эту формулу называют формулой полной вероятности. Доказательство. Так как гипотезы B1, B2,…,Bn образуют полную группу, то событие A может появиться только в комбинации с какой-либо из этих гипотез: A = B1A+B2A+…+BnA Так как гипотезы B1, B2,…,Bn несовместны, то и комбинации B1A, B2A,…,BnA также несовместны; применяя к ним теорему сложения, получим: Р(А) = Р(B1А)+Р(B2А)+…+ Р(BnА)= ∑ni=1P(BiA). Применяя к событию BiA теорему умножения, получим: P(A) =  что и требовалось доказать. что и требовалось доказать.Пусть событие А может наступить при условии появления одного из несовместных событий, образующий полную группу. Поскольку заранее не известно какое из этих событий наступит и их наз. гипотезами. Формула Баесса позволяет переоценить вероятности гипотез после того как становится известным результат испытания в итоге которого появилось событие А. Формула Байеса: РА(Bi)=  35. Схема испытаний Бернулли. Формула Бернулли. На практике часто решают задачи, связанные с многократно повторяющимися испытаниями (опытами). При этом представляет интерес исход не каждого отдельного испытания, а общее число появления события А в результате определённого числа опытов. Последовательность испытания наз. независимыми, если Р осуществления любого исхода в каждом n-ом испытании не зависит от реализации исходов предыдущих испытаний. Серию независимых испытаний с одной и той же вероятностью успеха Р=Р(А) наз. испытаниями или схемой Бернулли. Обозначим через  – вероятность появления m раз события А в серии n-независимых испытаний. Тогда справедлива формула Бернулли: – вероятность появления m раз события А в серии n-независимых испытаний. Тогда справедлива формула Бернулли: 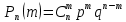 . Наступление события А наз. успехом, а не наступление события А наз. неудачей. Обозначим в-ть неудачи q=1-P(A)=(1-p). . Наступление события А наз. успехом, а не наступление события А наз. неудачей. Обозначим в-ть неудачи q=1-P(A)=(1-p). |
