Высш мат. Решение ду. Опред
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
7.Определение 3. Если y1 и y2 суть функции от х, то определитель называется определителем Вронского или вронскианом данных функций. Определитель Вронского имеет много различных свойств. Нам для доказательства теоремы об общем решении уравнения (3) потребуется следующее свойство: Теорема 3. Если определитель Вронского С его помощью мы докажем теорему: Теорема 4. Если y1 и y2 – два линейно независимых решения уравнения (3), то где С1 и С2 – произвольные постоянные, есть его общее решение. 8. теорема о структуре общего решения линейного однородного дифференциального уравнения второго порядка. доказательство Теорема 1. (о структуре общего решения линейного однородного дифференциального уравнения). Если функции Доказательство. В каждой точке указанной области имеет место существование и единственность решения задачи Коши. Покажем теперь, что функция 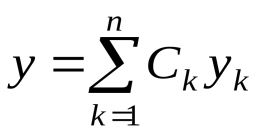 удовлетворяет определению общего решения уравненияп-го порядка. удовлетворяет определению общего решения уравненияп-го порядка.система уравнений 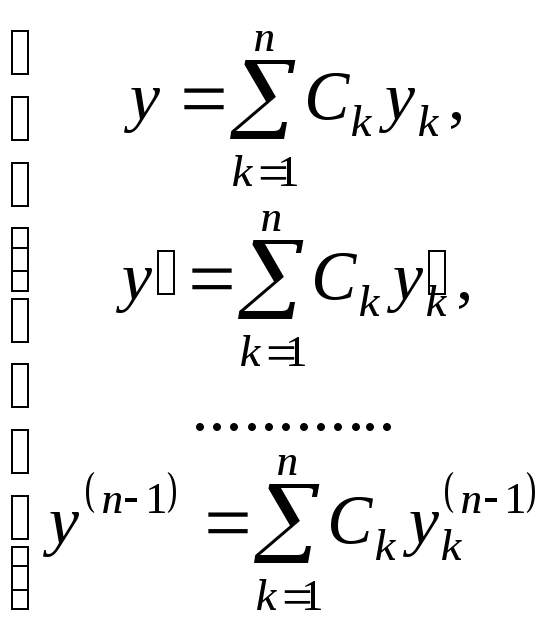 разрешима в области D относительно произвольных постоянных 2. Функция Поэтому функция 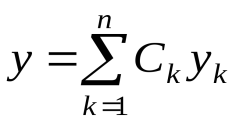 является общим решением уравнения является общим решением уравнения16. определение криволинейного интеграла второго рода.свойства,вычисление, применение Криволинейным интегралом II рода по координате x от функции f(x, y, z) по кривой L называется число 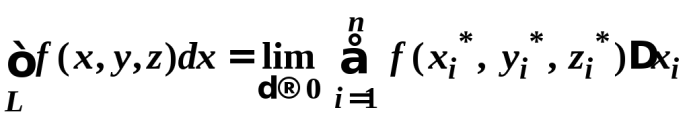 ,где – максимальная длина частей Li, если этот предел , не зависит от способа разбиения кривой и от выбора точекМi*. ,где – максимальная длина частей Li, если этот предел , не зависит от способа разбиения кривой и от выбора точекМi*.Условия существования криволинейного интеграла II рода. Достаточными условиями являются гладкость кривой и непрерывность интегрируемых функций. Свойства криволинейного интеграла II рода 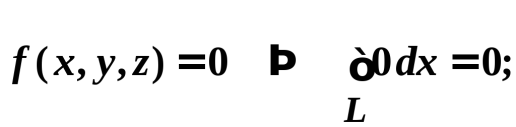 Линейность. Аддитивность. Интеграл «не замечает» изменения функции в конечном числе точек. Криволинейный интеграла II рода зависит от направления движения по кривой: Свойство следует из того, что при нумерации точек Мi с другого конца поменяют знак все разности xi=xi – xi-1. Если кривая L перпендикулярна оси Ox, то Применения криволинейного интеграла II рода. Работапеременной силы действующей на материальную точку при ее движении вдоль кривой L в заданном направлении: 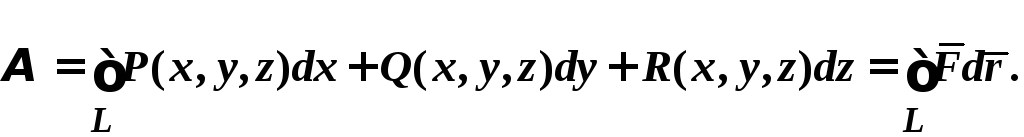 Работа силы равна сумме работ ее составляющих. 18. числовые ряды.сходимость ряда и его сумма Определение. Сумма членов бесконечной числовой последовательности 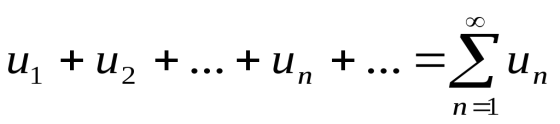 При этом числа Определение. Суммы 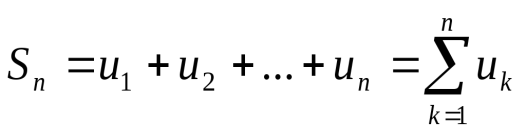 ,n = 1, 2, … называются частными (частичными) суммами ряда. ,n = 1, 2, … называются частными (частичными) суммами ряда.Таким образом, возможно рассматривать последовательности частичных сумм ряда S1, S2, …,Sn, … Определение. Ряд 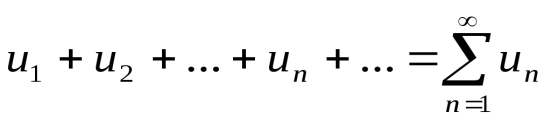 называетсясходящимся, если сходится последовательность его частных сумм. Сумма сходящегося ряда – предел последовательности его частных сумм. называетсясходящимся, если сходится последовательность его частных сумм. Сумма сходящегося ряда – предел последовательности его частных сумм.Определение. Если последовательность частных сумм ряда расходится, т.е. не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся и ему не ставят в соответствие никакой суммы. 21. ряд дирихле и его сходимость Обобщенным гармоническим рядом (или рядом Дирихле) называют ряд[1][3] В математикегармоническийрядпредставляет собой сумму, составленную из бесконечного количества членов, обратных последовательным числамнатурального ряда[1]: 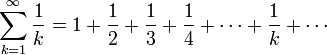 . .Исследуем ряд Дирихле на сходимость : 1) В случае, если , члены ряда образуют неубывающую последовательность, а сам ряд расходится по необходимому признаку сходимости ( 2) В случае для исследования сходимости ряда используем интегральный признак Коши. Введем функцию  в двух случаях а) , б) , т.е. когда : в двух случаях а) , б) , т.е. когда :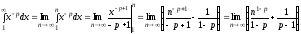 а) Если , , то 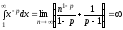 , следовательно, несобственный интеграл расходится и расходится исходный ряд. , следовательно, несобственный интеграл расходится и расходится исходный ряд.21.б) Если , , то 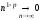 , тогда , тогда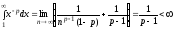 , следовательно, несобственный интеграл сходится и сходится исходный ряд. , следовательно, несобственный интеграл сходится и сходится исходный ряд.3) В случае имеем гармонический ряд 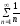 , для которого также применим интегральный признак Коши, т.е. рассмотрим интеграл , для которого также применим интегральный признак Коши, т.е. рассмотрим интеграл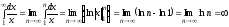 , следовательно, несобственный интеграл расходится, а значит, гармонический ряд расходится. , следовательно, несобственный интеграл расходится, а значит, гармонический ряд расходится.Вывод: ряд Дирихле 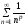 сходится, если , и расходится, если . сходится, если , и расходится, если .27. применение степенных рядов к приближенным вычислениям Используя разложение функций в степенные ряды Тейлора и Маклорена, можно приближенно вычислять, например, значения функций и приближенные значения определенных интегралов. Напомним, что рядом Тейлора для функции , если функция определена в окрестности точки и имеет в этой точке конечные производные, является степенной ряд: 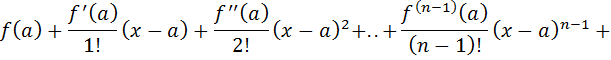 Чтобы функция была суммой этого ряда для значений x из некоторого промежутка, необходимо и достаточно, чтобы Чтобы функция была суммой этого ряда для значений x из некоторого промежутка, необходимо и достаточно, чтобы Если в ряде Тейлора положить , то получим ряд Маклорена: 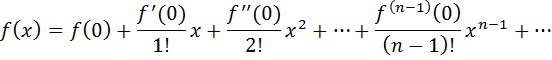 Обычно в задачах на приближенные вычисления используются ряды Маклорена для следующих функций: 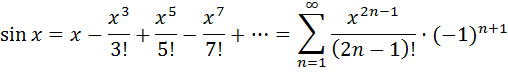 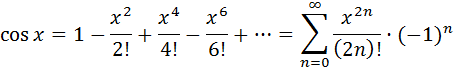 Области сходимости последних двух рядов также (-∞; +∞). 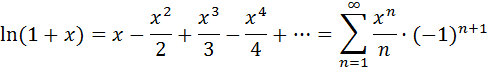 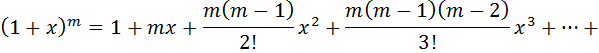 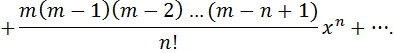 27.Можно показать, что область сходимости последних двух рядов . При , из последней формулы получим: 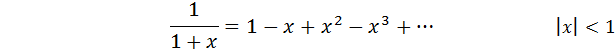 Если же x заменить на (-x) то получим формулу суммы бесконечно убывающей геометрической прогрессии: 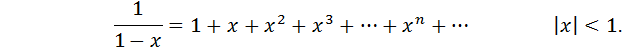 Пример: вычислить приближенно , взяв три члена разложения; оценить погрешность вычислений. Воспользуемся разложением в ряд Маклорена функции , положив . 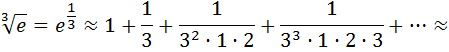 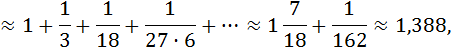 Погрешность вычислений: Если в задаче указано число членов разложения, то погрешностью вычислений будет первый отбрасываемый член разложения, в данном случае, - четвертый. 37. наивероятнейшее число появлений события при повторных испытаниях по схеме бернулли Наивероятнейшее число наступлений события при повторении испытаний. Наивероятнейшим числом mo появления события А в n независимых испытаниях называется число, для которого вероятность Рn (mo )превышает или, по крайней мере, не меньше вероятности каждого из остальных возможных исходов испытаний. Для определения наивероятнейшего числа наступлений события служит двойное неравенство: а) Если np-q дробное число, то и np+p тоже дробное. Так как mо - целое, то в этом случае будет одно наивероятнейшее число наступлений события. б) Если np-q целое, то и np+p целое, значит между ними нет целого промежуточного значения. В этом случае m принимает два значения: m1= np-q и m2= np+p. При очень большом числе независимых испытаний n - наивероятнейшая частота наступлений события близка к вероятности р этого события при отдельном испытании. 39. дискретные случайные величины и законы их распределения Случайной величиной называется числовая функция, определенная на пространстве элементарных событий Ω, которая каждому элементарному событию ω ставит в соответствие некоторое число. При этом предполагается, что определена вероятность события для любых значений x. Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Непрерывной называют случайную величину, которая может принимать все значения из некоторого промежутка. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически. При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения , а вторая – их вероятности
Существует универсальный способ задания закона распределения, который годится для случайных величин любого типа: функцией распределенияслучайной величины Х называется функция F(x), равная вероятности того, что Х примет значение меньше, чем число х, то есть Из определения следует, что |
