Эконометрика. ЖданЧАСТЬ 1.1. Тема Парный регрессионный анализ

• Название: Тема Парный регрессионный анализ
• Анкор: Эконометрика
• Дата: 09.11.2022
• Размер: 1.62 Mb.
• Имя файла: ЖданЧАСТЬ 1.1.doc
• Тип: Анализ; #778468
• страница: 1 из 10

Содержание
Введение 5

Тема 1. Парный регрессионный анализ

1. 
   Линейная парная регрессия и корреляция 8
   
2. 
   Коэффициент детерминации 12
   
3. 
   Реализация линейной регрессии в Microsoft Excel 14
   
4. 
   Индивидуальное задание 1 (ИЗ 1) Линейная парная
   

регрессия 20

5. 
   Образцы тестов к теме 1 32
   

Тема 2. Нелинейные модели регрессии

1. 
   Нелинейная парная регрессия 34
   
2. 
   Индивидуальное задание 2 (ИЗ 2) Построение моделей нелинейных регрессий 37
   
3. 
   Образцы тестов к теме 2 56
   

Тема 3. Множественный регрессионный анализ

1. 
   Множественный регрессионный анализ 59
   
2. 
   Оценка параметров уравнения множественной
   

регрессии. Парные коэффициенты корреляции. Частные коэффициенты корреляции 60

3. 
   Коэффициент детерминации и скорректированный коэффициент детерминации. Множественный коэффициент корреляции 62
   
4. 
   Анализ надежности результатов множественной регрессии и влияния факторов на результат в многофакторной регрессионноймодели 63
   
5. 
   Индивидуальное задание 3 (ИЗ 3) Отбор факторов в линейной модели множественной регрессии 66
   
6. 
   Образцы тестов к теме 3 81
   

Тема 4. Регрессионные модели с переменной структурой

1. 
   Использование фиктивной переменной для моделирования структурных изменений Проверка пригодности модели для прогнозирования. Гетероскедастичность 85
   
2. 
   Индивидуальное задание 4 (ИЗ 4). Исследование адекватности линейной регрессионной модели, использование фиктивной переменной для моделирования структурных изменений 86
   
3. 
   Образцы тестов к теме 4 101
   

Тема 5. Временные ряды и прогнозирование

1. 
   Методическиерекомендации 104
   
2. 
   Индивидуальное задание 5 (ИЗ 5) Прогнозирование на основе временных рядов 110
   
3. 
   Образцы тестов к теме 5 123
   

Тема 6. Системы одновременных уравнений

1. Общее понятие о системах уравнений. Структурная и приведенная формы модели 125

2. Проблема идентификации 128

3. Косвенный метод наименьших квадратов (КМНК) 130

4. Двухшаговый метод наименьших квадратов (ДМНК) 130

5. Трехшаговый метод наименьших квадратов (ТМНК) 133

6. Аудиторные задания 134

7. Индивидуальное задание 6 (ИЗ 6) Решение систем одновременных уравнений с помощью КМНК 135

8. Образцы тестов к теме 6 141

Теоретические вопросы к зачету 143

Рекомендуемая литература 145

Математико-статистические таблицы 146


ВВЕДЕНИЕ
Термин “эконометрика” был введен в 1926 г. норвежским ученым Р. Фришем и в дословном переводе означает “эконометрические измерения”.

Эконометрика возникла как результат взаимодействия и объединения трех составляющих: экономической теории, статистических и математических методов. Каждая из отправных точек – необходимое, но не достаточное условие для понимания количественных соотношений в современной экономической жизни.

ЭКОНОМЕТРИКА – наука, которая дает количественные выражения взаимосвязей экономических явлений и процессов.

Цель эконометрики – эмпирический вывод экономических законов. Специфическая особенность деятельности экономиста – работа в условиях недостатка информации и неполноты исходных данных. Анализ такой информации требует специальных методов, которые составляют один из аспектов эконометрики. В связи с этим центральной задачей является построение математической модели на основе эмпирических данных, оценивание неизвестных величин (параметров) в этих моделях, оценивание качества модели и прогнозирование реальных экономических процессов. Эконометрика рассматривает все эти вопросы, изучает способы решения поставленных проблем.

Типы моделей.

Можно выделить три основных класса моделей, которые применяются для анализа и прогноза.

Регрессионные модели с одним уравнением.

В таких моделях зависимая (объясняемая) переменная y представляется в виде функции

,

где - независимые (объясняющие) переменные, а - параметры. В зависимости от вида функции модели делятся на линейные и нелинейные. В зависимости от числа переменных модели делятся на парные и множественные. Например, можно исследовать спрос на мороженое как функцию от времени, температуры воздуха, среднего уровня доходов или зависимость зарплаты от возраста, пола, уровня образования, стажа работы и т.п.

Модели временных рядов.

К этому классу относятся модели:

тренда: , где - временной тренд заданного параметрического вида, - случайная компонента;

сезонности: , где - периодическая компонента; тренда и сезонности: (аддитивная) или (мультипликативная).

Общей чертой временных рядов является то, что они объясняют поведение временного ряда исходя только из его предыдущих значений. Такие модели могут применяться, например, для изучения и прогнозирования объема продаж авиабилетов, краткосрочного прогноза процентных ставок и т.п.

Системы одновременных уравнений.

Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых, кроме объясняющих переменных, может включать в себя объясняемые переменные из других уравнений. Примером может служить модель спроса и предложения.

Типы данных.

При моделировании экономических данных мы встречаемся с двумя типами данных:

• 
  пространственные данные (набор сведений по разным фирмам в один и тот же момент времени)
  
• 
  временные ряды (ежеквартальные данные по инфляции, средней заработной плате, национальному доходу и т.п.).
  

Широкому внедрению эконометрических методов способствовало появление во второй половине XX в. персональных компьютеров. Компьютерные эконометрические пакеты сделали эти методы более доступными и наглядными, так как наиболее трудоемкую работу по расчету различных статистик, параметров, характеристик, построению таблиц и графиков стал выполнять компьютер, а специалисту осталась творческая работа: постановка задачи, выбор соответствующей модели и метода ее решения, интерпретация результатов.

Для приобретения практических навыков реализации эконометрических моделей студенту рекомендуется:

-изучить приведенный в пособии теоретический материал по теме;

-выполнить индивидуальное задание по заданному варианту;

-оформить выводы в аналитической записке и защитить задание;

-ответить на вопросы теста.

ТЕМА 1. Парный регрессионный анализ

1. 
   . Линейная парная регрессия и корреляция
   

Уравнение связи двух переменных и , т.е. , называется уравнением парной регрессии, где - зависимая, объясняемая переменная (результативный признак), - независимая, объясняющая переменная (признак, фактор), - случайная составляющая.

Различают линейные и нелинейные регрессии. Линейная регрессия имеет вид: , где - параметры линейной регрессии.

Оценкой модели по выборке является уравнение регрессии . Параметры этого уравнения определяются на основе метода наименьших квадратов, который позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака от теоретических была бы минимальна, т.е. .

Необходимым условием существования минимума функции двух переменных является равенство нулю ее частных производных по неизвестным параметрам :

.

После преобразований получим систему для определения параметров , т.е. .

Выразим из первого уравнения последней системы. Получим .

Подставив выражение во второе уравнение системы, найдем , где - выборочная дисперсия переменной : , - выборочный корреляционный момент или выборочная ковариация:

.

Подставляя значение в уравнение регрессии , получим , или , где коэффициент называется выборочным коэффициентом регрессии (или просто коэффициентом регрессии) по .

Значения переменных могут быть измерены в отклонениях от средних значений, т.е. если обозначим через и - отклонения значений переменных от средних значений, то , где , . Уравнение регрессии в отклонениях примет вид: , а формула вычисления упростится:

.

В матричной форме линейная регрессионная модель имеет вид: , где , , .

Вектор оценок определяется по формуле: ( - матрица, полученная из матрицы транспонированием).

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции для линейной регрессии: ( ). Существуют и другие модификации формулы , которые можно получить из ранее изученных формул:

, .

Для оценки статистической значимости коэффициента корреляции используется - критерий Стьюдента (или _{фактическое}). Выдвигается гипотеза об отсутствии линейной корреляционной связи между и . При справедливости этой гипотезы статистика имеет -распределение Стьюдента с степенями свободы. Если , где (или _{фактическое}) - табличное значение - критерия Стьюдента, определенное на уровне значимости , при , то гипотеза отвергается, а, значит, коэффициент корреляции значим.

Воздействие неучтенных случайных факторов и ошибок наблюдений в модели определяется с помощью дисперсии ошибок и остаточной дисперсии .

Несмещенной оценкой дисперсии ошибок является выборочная остаточная дисперсия, которая определяется по формуле 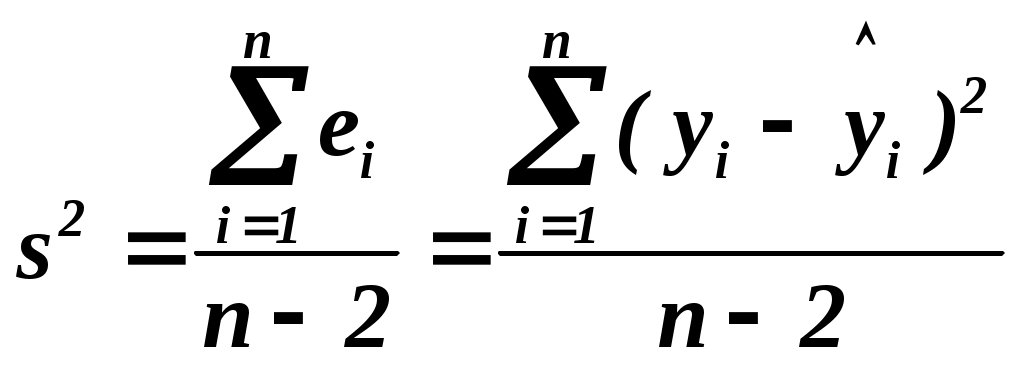, где - групповая средняя, найденная по уравнению регрессии; - выборочная оценка ошибки или остаток регрессии.

Оценка дисперсии групповых средних вычисляется по формуле: , где заменено ее оценкой .

Доверительный интервал для функции регрессии, т.е. для условного математического ожидания , который с заданной надежностью (доверительной вероятностью) накрывает неизвестное значение , вычисляется по формуле:

, где - стандартная ошибка групповой средней . Статистика имеет - распределение Стьюдента с степенями свободы.

Доверительный интервал для индивидуальных значений ( ) зависимой переменной вычисляется при условии, что нужно учитывать рассеяние вокруг линии регрессии, т.е. в оценку суммарной дисперсии следует включить величину . В результате оценка дисперсии индивидуальных значений , при равна , соответствующий доверительный интервал для прогнозов индивидуальных значений вычисляется по формуле:

,

а интервальная оценка параметра на уровне значимости имеет вид:

.

При построении доверительного интервала для параметра исходят из того, что статистика имеет - распределение с степенями свободы. Следовательно, интервальная оценка для параметра на уровне значимости имеет вид: .