| КАТЕГОРИЯ 1 | КАТЕГОРИЯ 1 |
1
|
Частная производная первого порядка функции  по переменной  равна:
|
1.  .
2.  .
3.  .
4.  .
|
2
|
Частная производная первого порядка функции  по переменной  равна:
|
1.  .
2. .
3. .
4. .
|
3
|
Вторая частная производная функции  по переменной  равна :
|
1.  .
2.  .
3.  .
4.  .
|
4
|
Полный дифференциал функции двух переменных  равен:
|
1.  .
2.  .
3.  .
4.  .
|
5
|
Вторая частная производная функции  по переменной равна:
|
1. .
2. .
3. .
4.  .
|
6
|
Полный дифференциал функции двух переменных  равен:
|
1. .
2. .
3. .
4.  .
|
7
|
Вторая смешанная частная производная функции  равна:
|
1. .
2.  .
3. .
4. .
|
8
|
Полный дифференциал функции двух переменных  равен:
|
1.  .
2. .
3. .
4. .
|
9
|
Частная производная первого порядка функции  по переменной равна:
|
1. .
2.  .
3.
4.  .
|
10
|
Вторая частная производная функции  по переменной  равна:
|
1. .
2. .
3.  .
4. .
|
11
|
Полный дифференциал функции двух переменных  равен:
|
1. .
2. .
3. .
4.  .
|
12
|
Частная производная первого порядка функции  по переменной равна:
|
1. .
2. .
3.  .
4. .
|
13
|
Вторая частная производная функции по переменной равна:
|
1.  .
2. .
3. .
4.  .
|
14
|
Функция  имеет локальный минимум в точке, если в некоторой окрестности этой точки: ( полное приращение заданной функции)
|
1. . 2.  . 3.  .
4. .
|
15
|
Область определения функции  представляет собой
|
1. квадрат  .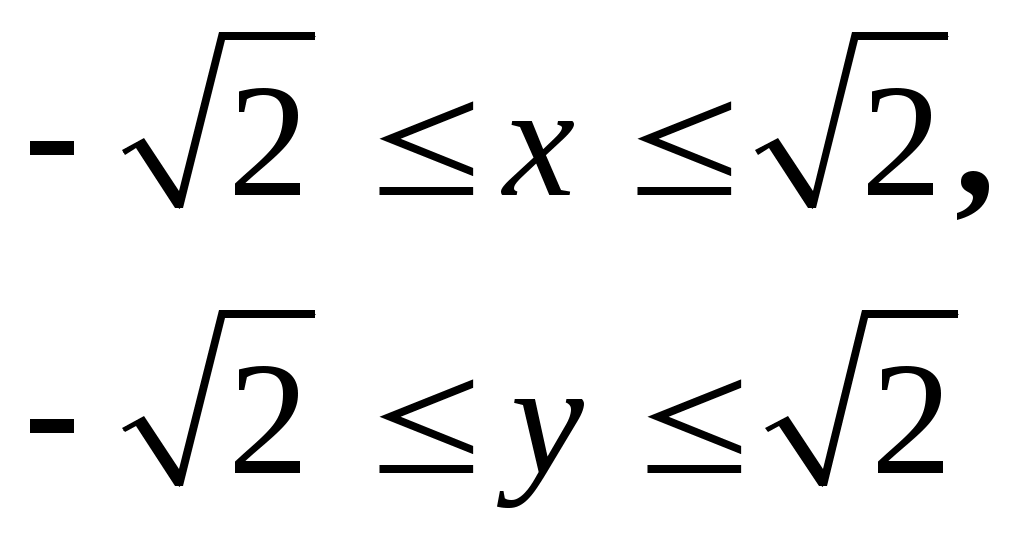
2.внешность круга радиуса  с центром в начале координат.
3. полоса  .
4. внутренность круга радиуса с центром в начале координат.
|
16
|
Касательная плоскость к поверхности  в точке гладкого экстремума:
|
1. параллельна плоскости ОYZ.
2. параллельна плоскости OXY.
3. перпендикулярна плоскости ОXZ.
4.перпендикулярна плоскости OXY.
|
17
| Градиент функции  равен: |
1.  . 2.  . 3. . .
4.  .
|
18
|
Производная функции  по направлению вектора  вычисляется по формуле:
|
1.  . 2.  .
3.  .
4.  .
|
19
|
Градиент функции нескольких переменных в точке задает направление:
|
1. наибольшего роста значений функции.
2. наименьшего роста значений функции.
4. положительных значений функции.
5. отрицательных значений функции.
|
20
| Дифференциал первого порядка функции  имеет вид |
1.  .
2.  .
3. .
4.  .
|
21
| Функция  дифференцируема в точке  , если ее полное приращение представимо в виде: |
1.  .
2.  .
3.  .
4.  ; -бесконечно малые.
|
22
| Формула для вычисления производной  функции , неявно заданной уравнением  , имеет вид: |
1.  . 2.  .
3.  . 4.  .
|
23
|
Предел функции  в точке (1,3) равен:
|
1. 1.
2.  .
3.  .
4.  .
|
Скачать 0.92 Mb.