основы технической механики. 1.1 Основы технической механики. 1. 1 Основы технической механики

Название	1. 1 Основы технической механики
Анкор	основы технической механики
Дата	12.10.2021
Размер	1.67 Mb.
Формат файла
Имя файла	1.1 Основы технической механики.docx
Тип	Документы #245957
страница	10 из 28

1 ... 6 7 8 9 10 11 12 13 ... 28

МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ

К твердому телу в точке A приложена сила F. Проведем в пространстве ось (например z). На оси z произвольно выберем точку ^O^.^{Соединим}^точкуO^с^точкой^А^{радиус-вектором. Через}^точкуOпроведем плоскость П перпенди-кулярную оси z. Спроектируем вектора Fи rна плоскость П .

^{Моментом}^силыF ^{относительно}^оси^{называется}^вектор^равный

^{моменту}^{проекции}^силыF ^на^{плоскость П}^{относительно}^точкиO

пересечения оси z с плоскостью П (Рис. 1.16)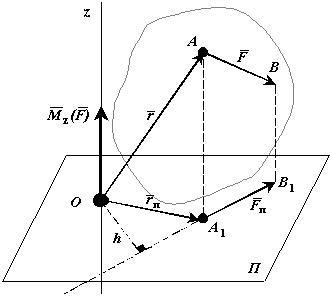

Рис. 1.16. Момент силы относительно оси.

^Mz⁽^F⁾^^M0 ⁽^FП⁾^^rП^^FП

^Mz⁽^F⁾^^FП^^rП^^sin(^rП^,FП⁾^^FП^^h
Свойства момента силы относительно оси:

Момент силы относительно оси равен нулю, если сила параллельна оси. В этом случае равна нулю проекция силы на плоскость, перпендикулярную оси.
Момент силы относительно оси равен нулю, если линия действия силы пересекается с осью. В этом случае равно нулю плечо силы.

СВЯЗЬ МОМЕНТА СИЛЫ ОТНОСИТЕЛЬНО ОСИ С МОМЕНТОМ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ

Проведем через точку O, где задан момент силы относительно

точки декартовы оси координат x,y,z. Момент силы

^M0⁽^F⁾

относительно точки можно представить в виде суммы трех

^{векторов}^M0 ⁽^F⁾^^Mx⁽^F⁾^^My⁽^F⁾^^Mz⁽^F⁾^.^Эти^{вектора}^{являются}моментами силы относительно осей x,y,z соответственно:

^Mx⁽^F⁾^^M0 x⁽^{F )}^ⁱ^My⁽^F⁾^^M0 y⁽^F⁾^^j^Mz⁽^F⁾^^M0 z⁽^F⁾^^k

Момент силы относительно оси равен проекции на эту ось момента силы относительно любой точки на оси.

		^Mz^{( F}⁾^^M0 ^{( F )}^^{cos( Oz,M}0 ⁽^F⁾⁾
Если	сила F	^задана^своими^{проекциями}^Fx^,^Fy^,	^Fz^на^оси
координат	и даны	координаты x, y, zточки приложения	этой силы,

относительно осей координат, то моменты силы относительно осей координат вычисляется следующим образом:

^Mx^{( F )}^^M0 x^{( F )}^^{( y}^^Fz^^z^^Fy⁾^My

⁽^{F )}^^M0 y^{( F )}^⁽^z^^Fx^^x^^Fz⁾

^Mz⁽^{F )}^^M0 z⁽^{F )}^⁽^x^^Fy^^y^^Fx⁾

1 ... 6 7 8 9 10 11 12 13 ... 28

основы технической механики. 1.1 Основы технической механики. 1. 1 Основы технической механики

МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ

СВЯЗЬ МОМЕНТА СИЛЫ ОТНОСИТЕЛЬНО ОСИ С МОМЕНТОМ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ