основы технической механики. 1.1 Основы технической механики. 1. 1 Основы технической механики
 Скачать 1.67 Mb.
|
СОЕДИНЕНИЕ ТЕЛ МЕЖДУ СОБОЙОтдельное тело может быть связано с другими телами разными способами. Опирание наповерхность.Если соприкасаются абсолютно гладкие тела, то силы взаимодействия между ними направлены по  общей нормали к их поверхностям в точке соприкосновения (рис.1.10).Рис. 1.10. Опирание на поверхность  Связь с помощью нитей (нить, цепь, трос). Связь, осуществляемая в виде гибкой нерастяжимой и невесомой нити, не дает удаляться телу от точки подвеса нити вдоль нити. Поэтому реакция натянутой нити также направлена вдоль нити, к точке ее подвеса (рис.1.11).
Рис. 1. 11. Связь с помощью нитей. Освободим гирю от связи разрезав (мысленно) нить в любом месте и добавив силу реакции связи, которую направим вдоль нити вверх (обозначим ее T ). Гиря становится свободным твердым телом на которое действуют две силы и при этом оно находится в покое. Согласно аксиоме о равновесии двух сил, силы P и T равны по величине и противоположны по направлению. ГЕОМЕТРИЧЕСКИЙ МЕТОД СЛОЖЕНИЯ СИЛ, ПРИЛОЖЕННЫХ В ОДНОЙ ТОЧКЕСилы называются сходящимися, если их линии действия пересекаются в одной точке. Различают плоскую систему сходящихся сил, когда линии действия всех данных сил лежат в одной плоскости, и пространственную систему сходящихся сил, когда линии действия сил лежат в разных плоскостях. На основании следствия из третьей аксиомы, силу можно переносить по линии ее действия. Рассмотрим плоскую систему сходящихся сил (рис. 1.12,а). Пользуясь следствием из третьей аксиомы, перенесем все силы в точку K . Такой перенос необходим для графического определения равнодействующей заданной системы сил. Выполнив этот перенос, получим четыре силы P1 , P2 , P3 , P4 приложенные к точке K. Для определения их равнодействующей сложим последовательно все данные силы, используя правило треугольника (рис. 1.12, б). Сложим
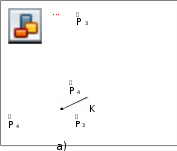 равную сумме сил P1 и P2 ,
 б)Рис. 1. 12. Сложение сил приложенных в одной точке: а)система сил, б)
, откуда
последовательно, в указанном выше порядке одну за другой отложить все заданные силы и начало первой соединить с концом последней. Полученная таким образом фигура OABCD называется силовым многоугольником. Замыкающая сторона этого многоугольника представляет собой равнодействующую R заданной системы сил, равную их геометрической сумме. Необходимо обратить внимание на то, что равнодействующая сила Rвсегда направлена от начала первого слагаемого к концу последнего слагаемого. Сложение данных сил возможно осуществить используя правило параллелограмма, но такой способ более трудоемок и громоздок. Если при построении силового многоугольника конец последней слагаемой силы совместится с началом первой, равнодействующая Rсистемы сходящихся сил окажется равной нулю. В этом случае система сходящихся сил будет находиться в равновесии. Замкнутость силового многоугольника данной системы сходящихся сил является геометрическим условием ее равновесия. Таким образом, для уравновешенной системы сходящихся сил вектор равнодействующей обращается в точку. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||