основы технической механики. 1.1 Основы технической механики. 1. 1 Основы технической механики

• Название: 1. 1 Основы технической механики
• Анкор: основы технической механики
• Дата: 12.10.2021
• Размер: 1.67 Mb.
• Имя файла: 1.1 Основы технической механики.docx
• Тип: Документы; #245957
• страница: 9 из 28

МОМЕНТ СИЛЫ ОТНОМИТЕЛЬНО ТОЧКИ И ОСИ

1. 
   МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ
   

Если под действием приложенной силы твердое тело может совершать вращение вокруг некоторой точки, то для того, чтобы охарактеризовать вращательный эффект силы, необходимо ввести новое понятие – момент силы относительно точки.

Рассмотрим	силу	F,	приложенную к телу в точке A. Из
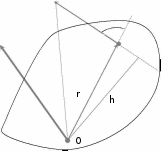некоторой точки	Oопустим перпендикуляр на линию действия силы
F(Рис. 1.15).
			B
			
	M0 (F)		F	
				A

Рис. 1.15. Момент силы относительно точки.




Плечомhсилы Fотносительно точки Oназывается кратчайшее расстояние между этой точкой и линией действия силы.

Через	силу	F		и точку Oможно провести плоскость.				Сила		F
пытается вращать тело вокруг оси, которая проходит через точку O											и
которая перпендикулярна плоскости в которой лежит сила.									Точка		O
называется моментнойточкой.
Моментом						силы	F относительно точки Oназывается вектор
M0 (F) , приложенный в этой точке и равный векторному произведению
радиус-вектора r				, соединяющего эту точку с точкой приложения силы,
на вектор силы		F.
							M 0 (F )  r F
Модульвектора							M0 (F) равен произведению модуля силы F				на
ее плечо h.
							M0 ( F )  F  r sin(  ) F  h
Момент	силы			F относительно точки Oнаправлен перпендикулярно

плоскости, в которой лежат сила и моментная точка (радиус-вектор), в

O

том направлении откуда видно стремление силы вращать тело против движения часовой стрелки.

Момент силы относительно точки не меняется от переноса силы вдоль линии ее действия. Момент силы равен нулю, если линия действия силы проходит через моментную точку.

^{Если сила F задана своими проекциями F}x ^Fy ^Fz ^{на оси}

координат и даны координаты xyzточки приложения этой силы, то момент силы относительно начала координат вычисляется следующим образом:

i j k _{y z}



z x x y

M₀ (F)  r  F

x y z

F

y

F_x F_y F_z

 i 


F F

z z

 j ^F

F

x x

 k

F

y

 ( y F_z z F_y)  i (z F_x x F_z)  j (x F_y y F_x)  k

Проекции момента на оси координат равны:

^M0 x^{(F) (y F}z^{ z F}y<sup>)

M</sup>0 y^{( F )  ( z F}x^{ x  F}z^{) M}0




z^{( F) ( x F}y^{ y  F}x⁾