основы технической механики. 1.1 Основы технической механики. 1. 1 Основы технической механики

• Название: 1. 1 Основы технической механики
• Анкор: основы технической механики
• Дата: 12.10.2021
• Размер: 1.67 Mb.
• Имя файла: 1.1 Основы технической механики.docx
• Тип: Документы; #245957
• страница: 8 из 28

ПРОЕКЦИЯ СИЛ НА ОСИ

1.4.1. ПРОЕКЦИЯ СИЛЫ НА ОСЬ
Часто геометрическое сложение векторов сил требует сложных и громоздких построений. В таких случаях прибегают к другому методу, где геометрическое построение заменено вычислениями скалярных величин. Достигается это проектированием заданных сил на оси прямоугольной системы координат.
Из математики известно, ось это неограниченная прямая линия, которая имеет определенное направление. Проекция вектора на ось является скалярной величиной, которая определяется отрезком оси, отсекаемым перпендикулярами, опущенными из начала и конца вектора на ось. Проекция вектора является положительной (+), если направление от начала проекции к ее концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной (-), если направление от начала проекции к ее концу противоположно положительному направлению оси.
Рассмотрим ряд случаев проектирования сил на ось.



1. 
   Дана сила P (рис.1.13, а) она лежит в одной плоскости с осью х. Вектор силы составляет с положительным направлением оси острый угол  .
   

а	а)	b	x	а	x b
x				x

б)

Рис. 1. 13. Проекция сил: а) с положительным углом, б)с отрицательным

Чтобы найти величину проекции, из начала и конца вектора силы проводим перпендикуляры на ось х; получаем:

P_x ab  P cos
Проекция вектора в данном случай является положительной.



2. 
   Дана сила Q(рис. 1. 13 б), которая лежит в одной плоскости с осью x, но ее вектор составляет с положительным направлением оси
   



тупой угол  . Проекция силы Qна ось x:
^Qx^{ ab Qcos , но cos  cos  .}
Так как  90⁰ , то cos - отрицательная величина. Выразим cos через

cos  , получим:
Q_x Qcos  .

Тогда проекция силы отрицательна.
Проекция силы на координатную ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси.

1.4.2 ПРОЕКЦИЯ СИЛЫ НА ОСИ ПЛОСКОЙ И ПРОСТРАНСТВЕННОЙ СИСТЕМЫ КООРДИНАТ

Силу, расположенную на плоскости xOy, можно спроектировать



на две координатные оси Oxи Oy. На рис. 1.14 изображена сила Pи ее ^{проекции P}x^{и P}y^.

y
b`				В
			
		(P, y)	P
Py	Py
(P, x)
a`
	А			С
		Px
О	a		Px	b	x
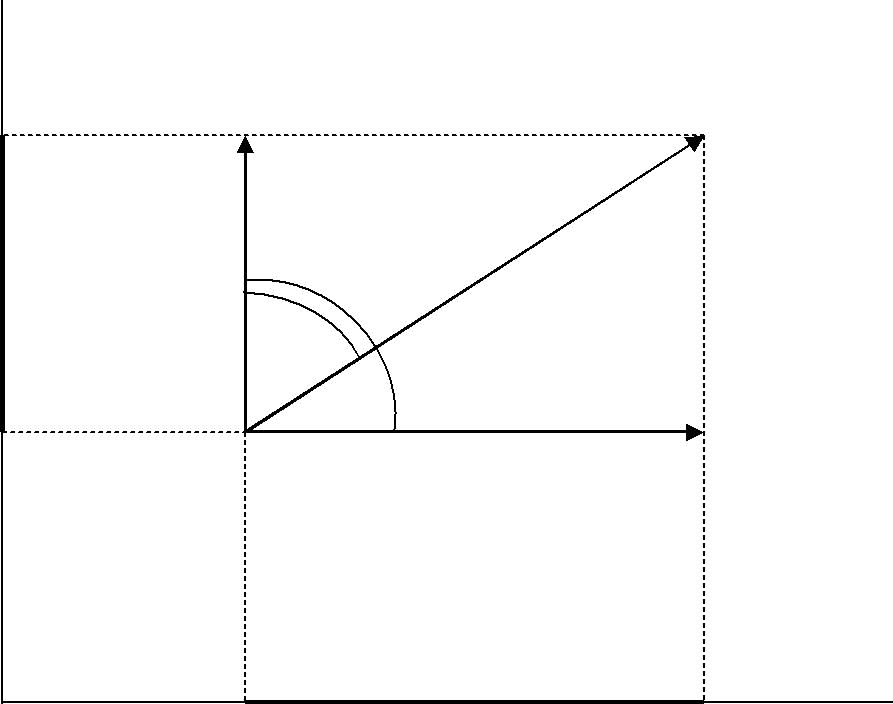Рис.1.14. проекция силы на оси плоской системы координат

Так как проекции образуют между собой прямой угол, из прямоугольного треугольника АВС следует:





^Px^


cos(P, x)  _

P



• 
  P
  


cos(P, y)  ^y

P 
Данными формулами можно пользоваться для определения величины и направления силы, когда известны ее проекции на оси координат. Эти формулы могут применяться для определения величины и направления любого вектора через его проекции.



На плоскости сила P может быть представлена как векторная сумма ^{двух взаимно перпендикулярных сил P}x^{и P}y^{, которые по модулю}

  

равны абсолютным значениям соответствующих проекций P Px Py.
Здесь имеет случай разложения силы на две составляющие по координатным осям. Отличие проекции силы от ее составляющих заключается в том, что проекция силы на ось – величина скалярная, а составляющая – величина векторная.

При рассмотрение силы в пространстве, приходится проектировать ее на три оси координат. Первоначально сила проектируется на координатные плоскости. Проекции сил на координатные плоскости представляют собой векторные величины.



Сила P может быть представлена диаганалью прямоугольного ^{параллелепипеда, построенного на составляющих P}x^{, P}y^{, P}z^{, которые по}

модулю равны соответствующим проекциям. Следовательно модуль и направление силы в пространстве определятся по формулам:

x y z
P P²  P²  P² ;

• 
  
  
  
  P _
  ^Pxcos( , x)
  

P



• 
  P
  


y

^{cos(P, y)} 

P


^Pz^




cos(P, z)  _

^P
Таким образом, в пространстве силу можно разложить на три составляющие по координатным осям:
   

^{P Px Py P}z