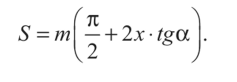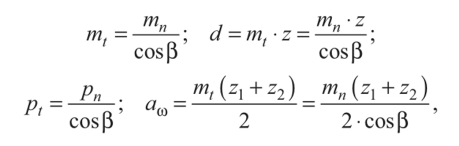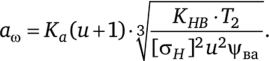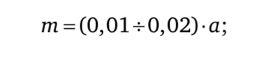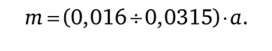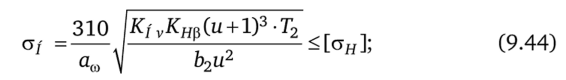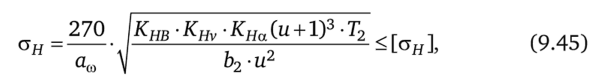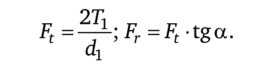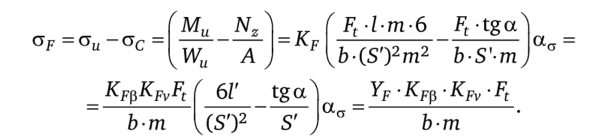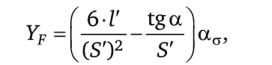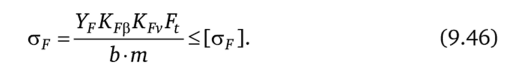|
|
1 деталь узел машина (определение) детали и узлы общего назначения
Основные характеристики передач:
Передаточное отношение u – кинематическая характеристика передачи, отношение входной и выходной скоростей передачи. Она показывает, во сколько раз уменьшается скорость передачи. Для передач, передающих вращательное движение:
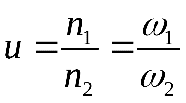 , ,
Где , – входная и выходная частота вращения передачи,
, – входная и выходная угловая скорость передачи;
Передаваемый момент mкр, н∙м, н∙мм – для передач, передающих вращательное движение;
Передаваемая мощность p, квт;
Передаваемые момент mкр и мощность p являются силовыми характеристиками и по ним оценивают нагрузочную способность передачи. В расчетах обычно используют только одну из этих характеристик.
Кпд – отношение полезной работы к затраченной. Разница между затраченной работой (на ведущем валу передачи) и полезной работой (на ведомом валу) характеризует внутренние потери механической энергии передачи (на преодоление трения, сопротивления качения). Величина кпд показывает, какая часть механической энергии передается дальше. Обычно кпд определяют через мощность:
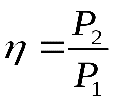 , ,
Где , – мощность соответственно на ведомом и ведущем валу передачи;
+
Быстроходность – скорости движения элементов передачи. В качестве общей характеристики обычно принимают частоту вращения (об/мин) илиугловую скорость 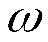 (рад/сек) валов передачи. Однако часто в расчетах для оценки прочности отдельных элементов передачи используют их линейную скоростьv (м/сек), например, линейную скорость движения зуба в зубчатых передачах, скорость движения ремня в ременных передачах или цепи в цепных передачах; (рад/сек) валов передачи. Однако часто в расчетах для оценки прочности отдельных элементов передачи используют их линейную скоростьv (м/сек), например, линейную скорость движения зуба в зубчатых передачах, скорость движения ремня в ременных передачах или цепи в цепных передачах;
Долговечность (ресурс), часов, лет– длительность работы передачи или отдельных ее элементов;
Габаритные размеры и масса.
6 энерго-кинематический расчет привода
Целью энерго-кинематического расчета судовой грузовой электрической лебедки является выбор электродвигателя по каталогу исходя из требуемой мощности и определение исходных данных для проектирования механических передач редуктора.
7 основные параметры зубчатых передач
К геометрическим параметрам зубчатых передач (рис. 3.11) относятся окружность диаметром da, ограничивающая вершины головок зубьев и называемая окружностью вершин зубьев; окружность диаметром d,, ограничивающая глубину впадин со стороны тела колеса и называемая окружностью впадин; окружность диаметром de, эвольвента которой является профилем зуба и называется основной окружностью.
Расстояние между одноименными профилями соседних зубьев по начальной окружности диаметром dw, называют начальным шагом pw. Длина окружности, по которой измерен шаг, pw • z = tzdw. Отсюда диаметр начальной окружности dw = (а,/я) • z = т ? Z. Отношение pw/п = т называется модулем.
Поскольку модуль определяется из прочностного расчета и технологическими условиями, а передаточное отношение - кинематикой привода. Уменьшение габаритов передачи может быть достигнуто уменьшением числа зубьев z шестерни. Нарезание зубьев шестерни (числом зубьев

Z < zmin, углом профиля а и коэффициентом высоты головки ha) без
Смещения зуборезного инструмента (коэффициент смещения х = 0) получаются подрезные зубья, прочность ножки зуба уменьшается, кроме того, уменьшается степень перекрытия зацепления. Для устранения подрезания режущий инструмент отодвигают от центра заготовки.
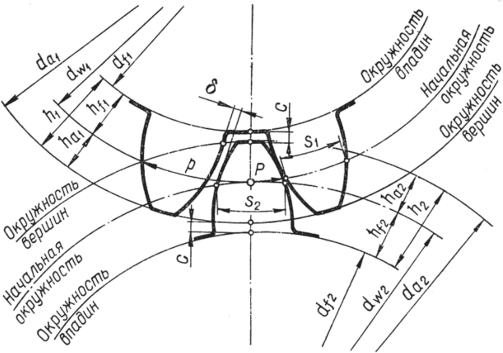
Рис. 3.11. Геометрические параметры зубчатой передачи
Если смещение применено для предотвращения подрезания ножки зуба, то коэффициент х шестерни определяют из условия
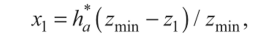
Где zmin =--— - наименьшее число зубьев, при котором нет подреза-
Sin а
Ния.
Кроме того, при выборе коэффициентов смещения х и х2 необходимо избежать интерференции зубьев, когда профили «накладываются» друг на друга и передача заклинивается.
В зависимости от величины коэффициента смещения различают зубчатые колеса и передачи со смещением и без смещения.
Передачи без смещения имеют -^ = х2 = 0. В таких передачах угол зацепления (х^ численно равен углу профиля исходного контура ос (рис. 3.12, а).
Передачи со смещением (рис. 3.12, б) образуются из колес, нарезанных со смещением. Если коэффициенты х и х2 равны по величине, а знаки их противоположны, то передача называется равносмсщснной (х^ = x] + х2 = 0). В такой передаче, как и в передаче без смещения, 0сю = (x. Если xj- ф 0, то в такой передаче со смещением угол зацепления
А№ а.
После определения коэффициентов смещения параметры передачи рассчитываются по следующим формулам:
- коэффициент суммарного смещения х^ = xj + х2;
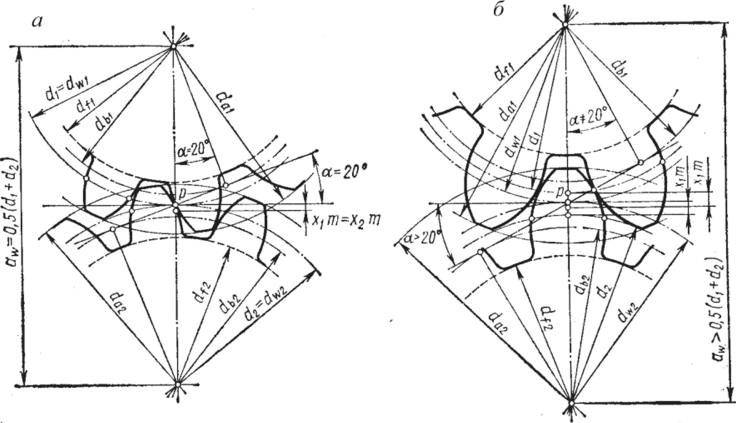
Рис. 3.12. Зубчатые передачи: а - без смещения; 6- со смещением
- угол зацепления аи;: inwdw = inva + 2xs • tga / (z, + z2);
- межоссвос расстояние зубчатой передачи
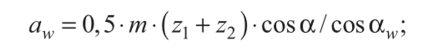
- делительные диаметры d = mz;
- диаметры начальных окружностей:
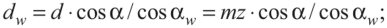
- диаметры окружностей впадин
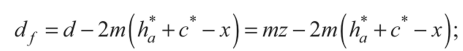
- диаметры окружностей вершин
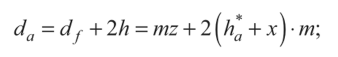
- диаметры основных окружностей 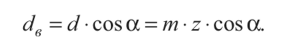 толщина зуба по делительной окружности толщина зуба по делительной окружности
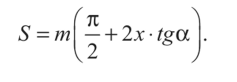
Высота зуба h = 0,5^da—dj-^, высота головки зуба
Ha = 0,5[da —d) и высота ножки зуба hja = 0,5(d-dy^.
В этих формулах па - коэффициент высоты головки зуба (для нор- * * *
Мальных зубьев ha = 1, для укороченных па = 0,8); с - коэффициент радиального зазора (если ha = 1, то для т> с = 0,25; для 0,5 < т < 1 с
= 0,35; для 0,1 < т < 0,5 с = 0,4).
Аналогично определяются геометрические параметры передач с косыми и шевронными зубьями. Картина зацеления косозубых колес в торцевой плоскости такая же, как для прямозубых колес, но параметры косозубого колеса в этой плоскости будут зависеть от угла наклона зубьев (3:
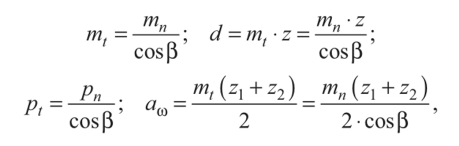
Где mt и pt - соответственно торцовые (окружные) модуль и шаг зубьев; тп и рп- то же в нормальном к оси зуба сечении.
Окружности вершин колес пересекают линию зацепления в точках а и в (рис. 3.13) и образуют отрезок. Вне отрезка ав касания сопряженных профилей не может быть, поэтому отрезок ав называется рабочей частью линии зацепления, или практической линией зацепления.
Дугой зацепления s называется путь, проходящий профилем зуба по начальной окружности за время фактического его зацепления.
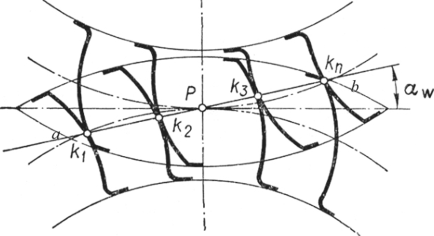
Рис. 3.13. Рабочая часть линии зацепления
Необходимыми условиями непрерывности зацепления являются требования, чтобы дуга зацепления была больше шага зацепления, т.е. S > р. Отношение дуги зацепления к шагу называется коэффициентом перекрытия ? = s / р. Коэффициент перекрытия характеризует собой среднее число пар зубцов, одновременно находящихся в зацеплении. Для цилиндрических прямозубых колес ? = 1,1.. .2,2; косозубых - ? = 3,0... 10,0.
8 принцип действия и классификация зубчатых передач достоинства и недостатки
принцип действия зубчатой передачи основан на зацеплении пары зубчатых колес.
по расположению осей валов различают:
Передачи с параллельными осями, которые выполняют с цилиндрическими колесами внешнего или внутреннего зацепления;
Передачи с пересекающимися осями - конические колеса;
Передачи с пересекающимися осями - цилиндрические винтовые, конические гипоидные, червячные. Кроме того, применяют передачи между зубчатым колесом и рейкой.
Основные достоинства зубчатых передач:
Высокая нагрузочная способность;
Надежность работы в широком диапазоне скоростей и нагрузок;
Большая долговечность;
постоянство передаточного отношения;
Высокий кпд.
Среди недостатков можно отметить:
Повышенные требования к точности изготовления;
Шум при высоких скоростях;
Высокую жесткость, не позволяющую компенсировать динамические нагрузки.
Отмеченные недостатки не снижают существенного преимущества зубчатых передач перед другими видами передач, что предопределяет их широкое применение в технике.
9.степени прочности зубчатых передач.
Стандартами предусмотрены 12 степеней точности зубчатых передач. Степени точности обозначаются в порядке их убывания от 1 до 12. В машиностроении и приборостроении наиболее часто применяют 6…9 степени точности. Быстроходные передачи и прецизионные механизмы иногда изготовляют по степени точности 5.
Для каждой степени точности установлены следующие нормы:
· кинематической точности;
· плавности работы;
· контакта зубьев.
Норма кинематической точности характеризуется наибольшей погрешностью передаточного отношения (u) за один оборот зубчатого колеса. Кинематическая точность связана с накопленной ошибкой шага и биением. Данный показатель важен для следующих типов передач:
· передач отсчетных и делительных цепей;
· передач, соединенных с большими массами;
· быстроходных силовых передач из-за опасности возникновения резонансных и других видов колебаний и шума.
Норма плавности работы характеризуется многократно повторяющимися за оборот зубчатого колеса колебаниями скорости, вызывающими динамические нагрузки, колебания и шум. Плавность работы связана с ошибками шага и профиля зуба. Данный показатель важен для силовых быстроходных передач.
Норма контакта зубьев характеризуется пятном контакта зубьев, показывающего на концентрацию нагрузки по ширине зубчатого венца. Данный показатель существенно влияет на работоспособность силовых передач.
Допускается комбинирование норм кинематической точности, плавности работы и контакта зубьев разных степеней точности.
10. Контактные напряжения и виды разрушений зубьев зубчатых колес под их воздействием.
Контактные напряжения , действующие в месте контакта зубьев
. - формула герца для определения контактных напряжений
Поломка зубьев – появляется из-за повторно-переломных напряжений изгиба. Прямые короткие зубья выламываются полностью, а длинные обламываются по косому сечению. Поломку зубьев предупреждает расчёт на прочность по напряжениям изгиба.
Усталостное выкрашивание рабочих поверхностей зубьев– возникает из-за действия повторно-переменных контактных напряжений. В местах постоянного контакта зубьев развивается наибольшая сила трения, появляются микротрещины, что ведёт к образованию маленьких ямок, переходящих в раковины. Предупреждают усталостное выкрашивание расчётом на прочность по контактным напряжениям.
Износ зубьев. По мере износа утончается зуб, увеличиваются зазоры в зацеплении, что ведёт к поломке зуба, появляется шум при работе передачи. Износ можно уменьшить защитой от
Попадания абразивных частиц, повышением твёрдости и класса чистоты рабочих поверхностей зубьев.
Излом зубьев.различают два вида излома зубьев. Излом от больших перегрузок, а иногда от перекоса валов и неравномерной нагрузки по ширине зубчатого венца и усталостный излом, происходящий от длительного действия переменных напряжений изгиба. Усталостные трещины образуются чаще всего у основания зуба (иногда трещина распространяется к вершине зуба) на той стороне, где от изгиба возникают напряжения растяжения. Для предупреждения усталостного излома применяют: колёса с положительным смещением при нарезании зубьев; термообработку; дробеструйный наклёп; жёсткие валы, увеличивают модуль и др.
Заедание зубьев.происходит привар частиц одного зуба к другому вследствие местного повышения температуры в зоне зацепления, срыва масляной плёнки. После чего происходит задир рабочих поверхностей зубьев. Заедание зубьев предупреждают повышением твёрдости и класса чистоты рабочих поверхностей зубьев, правильным подбором противозадирных масел.
11.силы в зацеплении прямозубой и косозубой цилиндрической передачи.
Цилиндрические косозубые передачи
- окружная сила;
- вспомогательная окружная сила;
- осевая сила;
- радиальная сила;
- сила нормального давления.
В прямозубой передаче в зоне зацепления действует нормальная сила , которая направлена по линии зацепления nn. Эту силу раскладывают на составляющие: окружную силу
И радиальную .при заданном моменте ,
12.расчет прочности зубьев прямозубой цилиндрической передачи по контактным напряжениям и напряжениям изгиба.
Основной причиной выхода из строя большинства зубчатых передач является усталостное выкрашивание рабочих поверхностей зубьев. Чтобы избежать этого, зубья рассчитывают на выносливость рабочих поверхностей по контактным напряжениям.
Контакт двух зубьев цилиндрических зубчатых колес рассматривается как контакт по двум образующим двух цилиндров и, следовательно, является линейным контактом. Наибольшие контактные напряжения (см. Рис. 9.20) возникают при соприкосновении зубьев в полюсе (в зоне однопарного зацепления прямозубых передач).
Расчет выполняют для зацепления в точке полюса, так как выкрашивание начинается у полюсной линии. В качестве исходной принимают формулу герца для определения контактных напряжений, возникающих при сжатии двух цилиндров, соприкасающихся по образующим. Приведем расчетные формулы без выводов.
Проектный расчет:
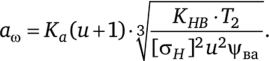
После определения межосевого расстояния а определяют модуль и округляют его значение до стандартного.
При твердости рабочих поверхностей:
• зубьев шестерни и колеса < нв 350 принимают:
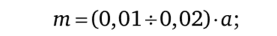
• зубьев шестерни >45 hrc и колеса < нв 350 принимают:
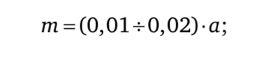
• зубьев шестерни и колеса >45 hrc принимают:
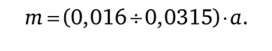
Учитывая возможное осевое смещение зубчатых колес при сборке передачи, ширину венца шестерни принимают на несколько миллиметров большей, чем ширину венца колеса.
Проверочный расчет:
• для прямозубых передач:
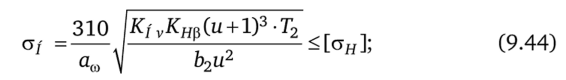
• для косозубых передач:
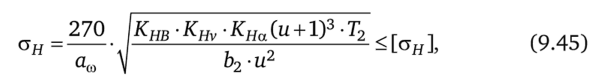
Где для прямозубых передач ка= 49,5, для косозубых передач ка = 43; и = г2/гг — передаточное число редуктора; кн^ — коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца; кна — коэффициент, учитывающий неравномерность распределения нагрузки между зубьями (для прямозубых передач кна = 1); khv — динамический коэффициент; fba — коэффициент ширины зубчатого венца относительно межосевого расстояния, ba = ъ2/ ам; [ан] — допускаемое контактное напряжение.
Расчет зубьев цилиндрических зубчатых передач на изгиб. С точки зрения прочности зубьев на изгиб наиболее опасен момент, когда зуб входит в зацепление или выходит из него, а сила нормального давления приложена к вершине зуба (рис. 9.21). При расчетах на изгиб зуб рассматривается как консольная балка, жестко защемленная одним концом, для которой справедлива гипотеза плоских сечений. Кроме того, полагаем, что вся нагрузка fn воспринимается только одним зубом, и пренебрегаем силами трения.
Прямозубая передача.
Силу fn перенесем по линии ее действия на ось симметрии зуба в точку л и разложим на две взаимно перпендикулярные составляющие:
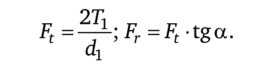
Зуб испытывает сложное сопротивление: сжатие и поперечный изгиб (сила ft изгибает зуб, а сила fr сжимает зуб). Строим эпюры продольных сил, изгибающих моментов и поперечных сил. Опасное сечение зуба — у заделки. Анализируем распределение напряжений по опасному сечению. Опасная точка в этом сечении — точка а (с микротрещины в точке а на рабочей стороне начинается процесс усталостной поломки зуба).
Неравномерность распределения нагрузки по длине контактной линии учтем коэффициентом kfр, динамические нагрузки — коэффициентом kfv.
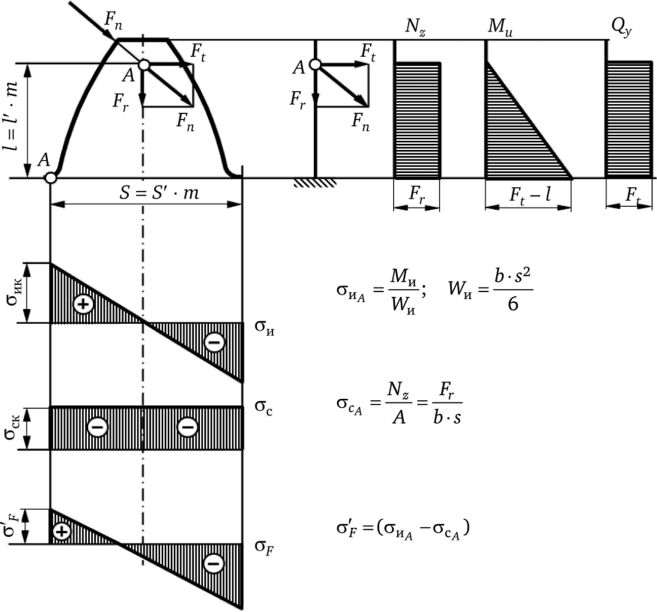
Рис. 9.21. Схема расчета зубьев на изгиб
Напряжение в точке а обозначим через af.
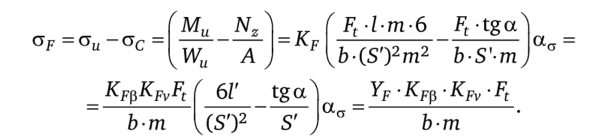
Введем обозначение
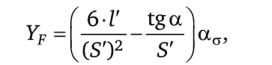
Где kf — коэффициент нагрузки, kf = kfр • kfv; [of] — допускаемое напряжение; yf — коэффициент формы зуба, зависящий только от числа зубьев и выбираемый по стандарту или справочной литературе.
Таким образом:
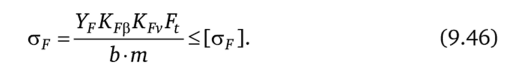
Формулы (9.44)—(9.45) используются для проверки зуба зубчатой передачи на прочность.
13
14
15
16
17
18
19
20
21. Передаточное число и кпд многоступенчатых редукторов и приводов состоящих из нескольких передач.
Как правильно рассчитать передаточное число
Передаточное число многоступенчатого редуктора вычисляется как произведение передаточных чисел каждой ступени. Пример. В редукторе четыре зубчатые пары, передаточные отношения каждой из которых тоже равны 4. Общее передаточное число тогда будет равно 4х4х4х4 = 256.
В общем случае общее передаточное отношение редуктора равно отношению частоты вращения входного (ведущего) вала и частоты вращения ведомого (выходного) вала. Отсюда следует, что если выходной вал вращается медленнее входного, то передаточное отношение будет больше единицы. Такие передачи называют понижающими. Если же скорость выходного вала будет выше скорости входного вала, то передаточное число будет меньше единицы. В этом случае говорят о повышающей передаче или мультипликаторе.
При передаче движения всегда соответственно меняется и крутящий момент: если передача понижающая, то момент увеличивается, если повышающая, то уменьшается. Поэтому передаточное число можно представить как отношение крутящего момента на выходе к крутящему моменту на входе в редуктор.
Расчёт без учета сопротивления
Любой редуктор состоит из зубчатых пар. Чтобы рассчитать передаточное число каждой пары, надо разделить количество зубьев ведущего колеса на количество зубьев ведомого колеса.
Кпд зубчатой передачи
Преимуществами данной передачи считаются:
Большая и неограниченная мощность.
Небольшая масса и габариты.
Большой коэффициент полезного действия (приблизительно 0,95-0,99).
Надёжны, но нуждаются в большой точности изготовления.
Кпд определяется как отношение реально полученной энергии к потребленной. Чем выше кпд механизма, тем больше энергии преобразовывается на полезные цели, тем меньше потери, тем эффективнее механизм.
Постоянное и переменное передаточное отношение редуктора
Передаточное отношение может быть как постоянным, так и переменным. При переменном случае оно может меняться бесступенчато или ступенчато. В промышленности нашли применение обе эти схемы. Если передаточное число меняется плавно, то такое устройство называют вариатором. Эти устройства дороги и требуют точной сборки и квалифицированного обслуживания. Но всё это оправдывается конечным результатом - их полезность уже проверена временем.
Расчет без учета сопротивления
В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.
U12 = ± z2/z1 и u21 = ± z1/z2,
Где u12 – передаточное число шестерни и колеса;
Z2 и z1 – соответственно количество зубьев ведомого колеса и ведущей шестерни.
Знак «+» ставится, если направление вращения не меняется. Это относится к планетарным редукторам и зубчатым передачам с нарезкой зубцов по внутреннему диаметру колеса. При наличии паразиток – промежуточных деталей, располагающихся между ведущей шестерней и зубчатым венцом, направление вращения изменяется, как и при наружном соединении. В этих случаях в формуле ставится «–».
Вычисление передаточного числа редуктора с несколькими зацеплениями – многоступенчатого, определяется как произведение передаточных чисел и вычисляется по формуле:
U16 = u12×u23×u45×u56 = z2/z1×z3/z2×z5/z4×z6/z5 = z3/z1×z6/z4
Передаточное отношение редуктора вычисляется по формуле:
U12 = ±ω1/ω2=±n1/n2
Где u12 – передаточное отношение шестерни относительно колеса;
Ω1 и ω2 – угловые скорости ведущего и ведомого элемента соединения;
N1 и n2 – частота вращения.
22. Критерии работоспособности и расчета ременных передач
Основным критерием работоспособности ременных передач является тяговая способность – надежность сцепления ремня со шкивом и долговечность ремня, которая зависит в основном от сопротивления усталостному разрушению.
Тяговая способность ременной передачи оценивается по кривым скольжения и кпд (рисунок 5.5). Эти кривые устанавливают зависимость коэффициента относительного скольжения ε и к.п.д. Передачи η от полезной нагрузки, которую выражают через коэффициент тяги ψ.
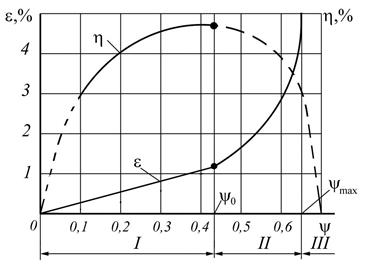
Рисунок 5.5 – кривые скольжения и к.п.д. Ременной передачи.
Коэффициент тяги показывает, какая часть предварительного натяжения ремня полезно используется для передачи нагрузки:
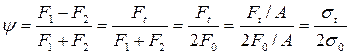 . .
|
(5.25)
|
Кривые скольжения для всех типов ремней получают экспериментальным путем при υ1 = 10 м/с и α = 1800. При постоянном натяжении 2f0 постепенно повышают полезную нагрузку ft и, соответственно, коэффициент тяги ψ. При этом на участке i наблюдается упругое скольжение ремня, на участке ii – частичное буксование, на участке iii – полное буксование. Критический коэффициент тяги ψ0 соответствует пределу рационального использования ремня и наибольшей нагрузке на ремень
Для плоских ремней коэффициент ψ0 = 0,4 ÷ 0,5, а для клиновых – ψ0 = 0,7 ÷ 0,8.
Так же критическому коэффициенту тяги соответствует максимальный к.п.д., который для плоскоременных передач составляет 0,93 ÷ 0,98, а клиноременных – 0,95 ÷ 0,98.
Расчет на долговечность выполняют как проверочный. За основу принято уравнение наклонного участка кривой усталости веллера
Где m и с – постоянные, определяемые экспериментально; σmax – максимальное напряжение цикла; ne – эквивалентное число циклов нагружения за срок службы ремня
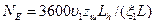 , ,
|
(5.28)
|
Где υ1 – скорость ремня; zш – число шкивов; lh – ресурс ремня; ζ1 – коэффициент; l - длина ремня.
Расчет ремней на долговечность требует накопления экспериментальных данных о параметрах кривой усталости для резино-тканиевого материала. В этой связи он применяется не для всех типов ременных передач.
Чаще на практике определяют число пробегов ремня в единицу времени
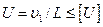 , ,
|
(5.29)
|
Где [u] – допустимое число пробегов.
Для плоскоременных передач [u] = 3 ÷ 5 с-1, для клиноременных – [u] = 10 ÷ 15 с-1. Для большинства ременных передач срок службы составляет 2000 ÷ 3000 часов.
23. Кинематические параметры ременных передач
В ременных передачах наблюдается два вида скольжения ремня по шкивам: упругое скольжение и буксование.
Упругое скольжение происходит при любой нагрузке, а буксование только при перегрузке. Упругое скольжение вызвано разностью натяжений ведущей и ведомой ветвей, создаваемой нагрузкой. Дуги упругого скольжения ас (рис. 15.4) располагаются со стороны сбегающей ветви. Положение точки с определяется из условия равенства окружной силы ( ) и суммарной силы трения, приложенной к ремню на дуге ас.
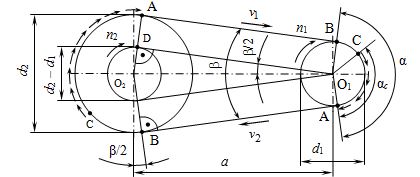
Рис. 15.4. Параметры двушкивной ременной передачи
На дуге вс ремень остается в состоянии покоя. Эту дугу называют дугой покоя. Сумма дуг упругого скольжения и покоя равна дуге обхвата, определяемой углом α.
С увеличением окружной силы дуга упругого скольжения возрастает, а дуга покоя уменьшается. При достижении значения, равного запасу сил трения, дуга покоя станет равной нулю, а дуга упругого скольжения распространится на всю дугу обхвата. В результате равновесие нарушается и происходит буксование.
Окружные скорости на шкивах (см. Рис. 15.4) определяются по формулам:
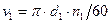 ; ; 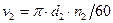 , ,
Где – диаметры, соответственно, ведущего и ведомого шкивов, м; – частоты вращения, соответственно, ведущего и ведомого шкивов, об/мин.
Из-за наличия упругого скольжения ремня по шкивам или
,
Где – коэффициент относительного скольжения.
Коэффициент относительного скольжения определяется как разность относительных удлинений ведущей ( )и ведомой ( ) ветвей ремня:
.
С учетом закона гука ( ) имеем:
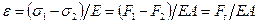 , (15.1) , (15.1)
Где – напряжения от натяжений соответственно ведущей ( ) и ведомой ( ) ветвей ремня; е – модуль продольной упругости материала ремня; еа – жесткость сечения ремня при деформации растяжения; а – площадь поперечного сечения ремня.
Из формулы (15.1) видно, что значение ε зависит от нагрузки , поэтому в ременной передаче передаточное отношение не является строго постоянным:
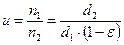 . (15.2) . (15.2)
При нормальных рабочих нагрузках :
· для прорезиненных плоских ремней ;
· для кожаных ремней ;
· для кордтканевых клиновых ремней ;
· для кордошнуровых клиновых ремней .
24. Конструкция и геометрические параметры ременных передач
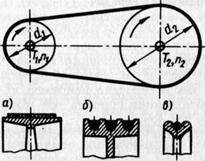
Основными геометрическими параметрами ременной передачи являются (рис. 11.14): углы обхвата на ведущем (ocj) и ведомом (а2) шкивах; межосевое расстояние (я); длина ремня (г); диаметры ведущего (d{) и ведомого (d2) шкивов.
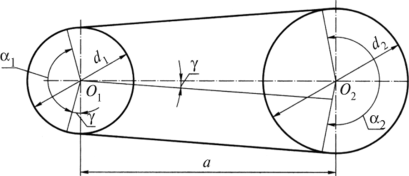
Рис. 11.14. Геометрические параметры ременной передачи
За расчетные диаметры dx и d2 принимают наружные диаметры плоских шкивов или диаметры расположения нейтральной линии ремня у шкивов для клинового и поликлинового ремней.
Диаметр ведущего шкива, мм, для плоскоременной передачи, а также для передач с клиновыми и поликлиновыми ремнями определяется отношением
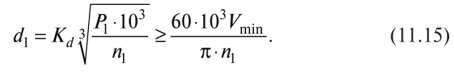
Здесь kd= по... 130 — для плоских ремней; kd= 80...90 — для клиновых ремней нормального сечения; kd = 50 — для узких клиновых ремней; kd = 65 — для поликлиновых ремней; р, — мощность на ведущем шкиве, квт; пх— частота вращения ведущего шкива, мин-1; vmin — минимально допустимая скорость для низкоскоростных передач (для плоских ремней vmin = 5 м/с, а для клиновых и поликлиновых ремней vm[n = 3 м/с).
Диаметр ведомого шкива:

Где и = пх/п2 передаточное число; ? — коэффициент скольжения ремня, ?, = 0,01 ...0,02.
Расчетные диаметры шкивов обычно округляются до ближайших стандартных значений. При этом допустимая погрешность передаточного числа аи < 5%.
Для плоскоременных передач межосевое расстояние выбирается по условию

(коэффициент 1,5 принимается для быстроходных передач).
Для передач с поликлиновыми и клиновыми ремнями межосевое расстояние выбирается с учетом следующих пределов:
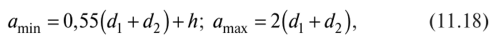
Где h — высота сечения ремня.
Длина ремня с учетом предварительно выбранного межосевого расстояния а' определяется зависимостью
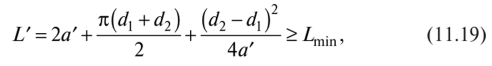
Где lmin — минимально допустимая из условия сравнительной долговечности длина ремня (см. Формулу 11.33).
Если длина ремня не удовлетворяет принятому условию, то ее следует увеличить. Расчетная длина бесконечных ремней округляется до большего стандартного значения.
Для окончательно выбранной длины ремня 1 уточняется межосевое расстояние
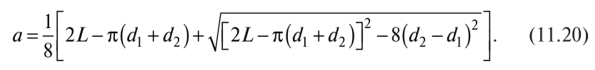
При конструировании передачи для компенсации вытяжки ремня должна предусматриваться возможность изменения межосевого расстояния в сторону его увеличения до следующих значений: а а = (0,03...0,05)1 — для плоских ремней; а а = (0,02)1 — для клиновых и поликлиновых ремней.
Угол обхвата ремнем ведущего шкива (рис. 11.15)
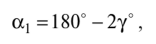
Где 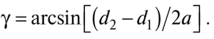
Применив разложение в ряд маклорена, получим 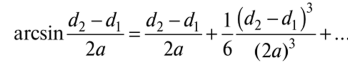
При у (d2 — dx)/2a угол обхвата
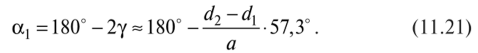
Для плоских прорезиненных ремней оц > 150°, для синтетических ремней oq > 120°, для клиновых и поликлиновых ремней >120°, но допустимы и утлы обхвата до 90°.
25. Силы и силовые зависимости в ременной передаче.
Передача состоит из двух шкивов, закрепленных на валах, и ремня, охватывающего шкивы. Нагрузка передается силами трения, возникающими между шкивами и ремнем вследствие натяжения последнего.
В зависимости от формы поперечного сечения ремня различают: плоскоременную (а), клиноременную (б) и кругло-ременную (в) передачи.
По сравнению с другими типами передач ременная обладает рядом особенностей, которые определяют целесообразность ее применения. Основными недостатками ременной передачи являются: повышенные габариты некоторое непостоянство передаточного отношения, вызванное зависимостью скольжения ремня от нагрузки; повышенная нагрузка на валы и их опоры, связанная с большим предварительным натяжением ремня низкая долговечность ремней. Ременные передачи применяют преимущественно в тех случаях, когда по условиям конструкции валы расположены на значительных расстояниях. В современном машиностроении наибольшее распространение имеют клиновые ремни.
Силы и силовые зависимости
На рис. 7.5 показано нагружение ремня в двух случаях: и т > 0.
По условию равновесия шкива имеем
,
Или
. (7.2)
Геометрическая длина ремня не зависит от нагрузки и остается неизменной как в ненагруженной, так и в нагруженной передаче. Следовательно, дополнительная вытяжка ведущей ветви компенсируется равным сокращением ведомой ветви. В соответствии с этим имеем
; , или , (7.3)
Где – начальное натяжение ремня; – изменение натяжений ведущей и ведомой ветвей ремня.
Из равенств (7.2) и (7.3) следует:
. (7.4)
Уравнения (7.4) устанавливают изменение натяжений ведущей и ведомой ветвей ремня в зависимости от нагрузки , но не вскрывают тяговой способности передачи, связанной со значением силы трения между ремнем и шкивом. Такая связь установлена эйлером:
; ; , (7.5)
Где – угол скольжения (см. Рис. 7.4); – коэффициент трения; – в данном случае рабочее начальное натяжение ремня.
Формулы (7.5) позволяют определить минимально необходимое начальное натяжение ремня , при котором еще возможна передача заданной нагрузки .
Из формул (7.5) следует, что увеличение значений и благоприятно сказывается на работе передачи. Эти выводы приняты за основу при создании конструкций клиноременной передачи и передачи с натяжным роликом.
При круговом движении ремня со скоростью возникает дополнительное натяжение ремня от центробежных сил, н:
,
Где – плотность материала ремня, кг/м3; а – площадь поперечного сечения ремня, м2.
Натяжение ослабляет полезное действие предварительного натяжения : уменьшает силу трения и, соответственно, уменьшает тяговую способность передачи. Влияние центробежных сил на работоспособность передачи существенно при скоростях > 20 м/с.
26. Натяжение ременных передач
Условием нормальной работы ремённых передач является наличие натяжения ремня, которое осуществляют следующими способами.
Предварительным упругим растяжением ремня.
Перемещением одного из шкивов относительно другого.
Натяжным роликом.
Автоматическим устройством, обеспечивающим регулирование натяжения ремня в зависимости от передаваемой нагрузки.
Перешивкой конечного ремня.
Механический (винтовой) способ.
Простые передачи — передачи с большим межосевым расстоянием и с натяжением от собственной массы ремня (рис. 10) и с натяжением за счет упругих деформаций ремня (рис. 11), надеваемого на шкивы с предварительным натягом.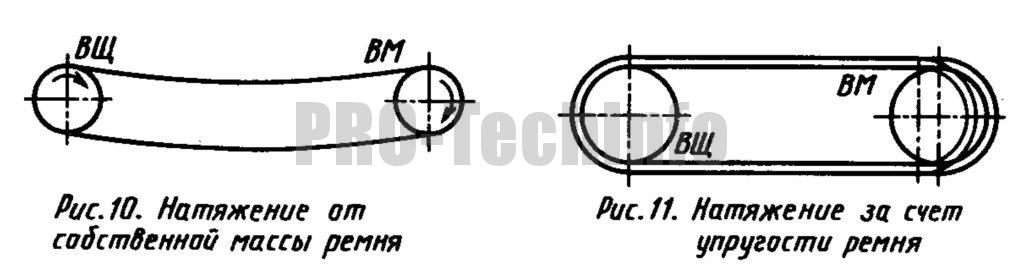
Натяжные передачи — натяжение осуществляется периодически перемещением одного из валов (рис. 12) или переставным роликом (рис. 13).
Самонатяжные передачи. Этот вид передач с автоматическим натяжением в наибольшей степени отвечает современным требованиям. Самонатяжные, как и натяжные передачи, применяют при малых межосевых расстояниях.
Пружинное натяжение.
К самонатяжным относят передачи с постоянным и переменным натяжением. Постоянное натяжение создается грузом (рис. 14) или пружиной (рис. 15)
Натяжение с помощью ролика.
Обособленно в этой группе стоит передача с натяжным роликом (рис. 16), качающимся на рычаге относительно неподвижной оси и прижимаемым к ремню пружинок или грузом. Натяжной ролик устанавливается на ведомой ветви и увеличивает углы охвата шкивов, что способствует улучшению тяговой способности передачи.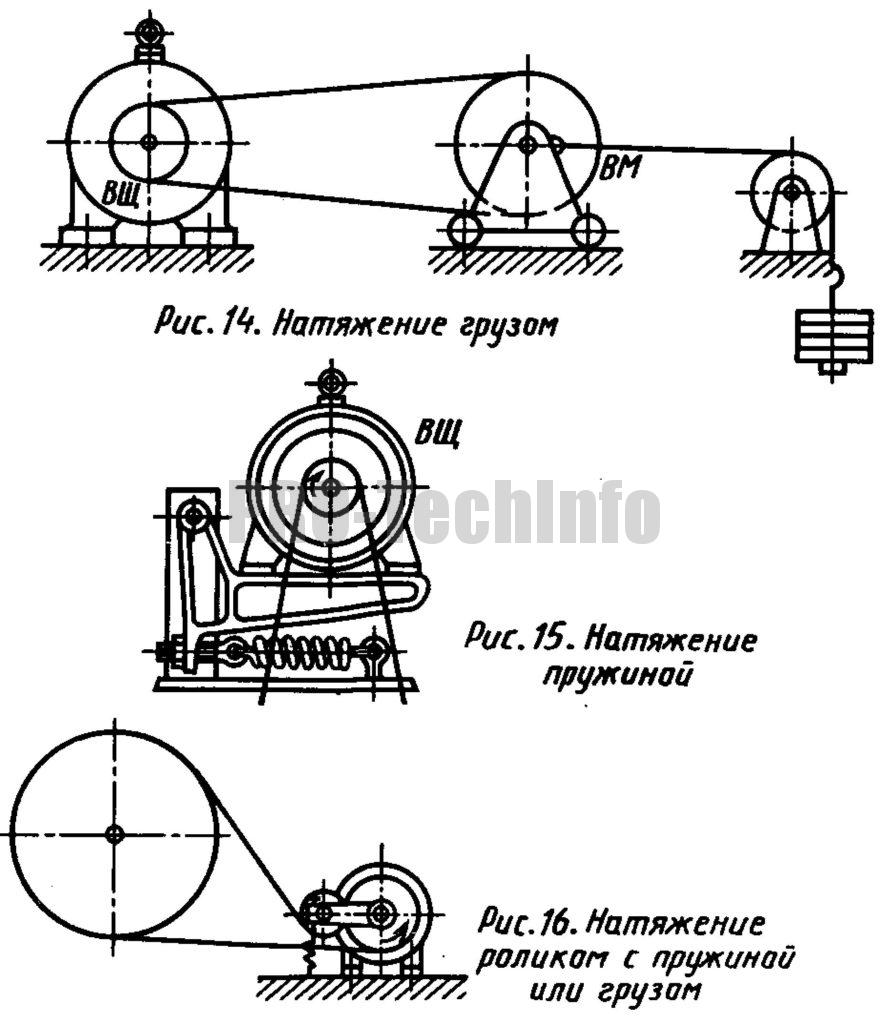
В передачах с переменным натяжением натяжение автоматически регулируется, увеличиваясь с ростом передаваемой мощности, что создает наилучшие условия для работы ремня и увеличивает кпд передачи. В таких передачах долговечность ремней возрастает.
Автоматическое натяжение.
В передаче с автоматическим натяжением ремня (рис. 18) на валу электродвигателя насажены ведущее зубчатое колесо и качающееся звено, на ось которого надеты ведомое зубчатое колесо и ременный шкив. При вращении ротора электродвигателя по часовой стрелке на качающееся звено действует момент от окружного усилия на шестерне, создающий в ременной передаче натяжение, пропорциональное передаваемому моменту. Возможен привод с механизмом автоматического натяжения ременной передачи с аналогичным устройством на ведомом шкиве. Представлена передача с натяжением ремня под действием реактивного момента, возникающего на корпусе качающегося электродвигателя. Сила натяжения зависит от эксцентриситета оси качания двигателя относительно оси шкива.
27. Нагрузка на ремни и опоры в ременной передачи
Повышенная нагрузка на валы и их опоры, связанное с большим предварительным натяжением ремня (в 2-3 раза больше, чем у зубчатых передач); низкая долговечность ремней (1000-5000 часов).
Скольжение ремня.
В ременной передаче возникают два вида скольжения ремня по шкиву: упругое - неизбежное при нормальной работе передачи и буксование - при перегрузке.
нагрузки валов (усилия в зубчатых и червячных зацеплениях, натяжения ветвей ременных и цепных передач, неуравновешенные составляющие окружных усилий, передаваемых муфтами) рассматривают как сосредоточенные силы, приложенные в серединах соответствующих деталей (зубчатых колес, шкивов и т. П.).
нагрузки валов зубчатых и червячных передач определяются усилиями, возникающими в зацеплении в ременных и цепных передачах валы испытывают нагрузки от натяжения ветвей. Нагрузка передается силами трения, возникающими между шкивами и ремнем. В качестве гибкой связи в передачах применяют плоские, клиновые, поликлиновые и круглые ремни.
У ременных передач трением сила r в два-три раза превышает окружное усилие у зубчато-ременных передач требуется незначительное предварительное натяжение ремня, поэтому нагрузка на валы немного больше окружного усилия, что является существенным достоинством этих передач.
28. Расчёт ременных передач (плоскоремённых и клиноременных)
Исходными данными для расчета ременных передач открытого типа (оси валов параллельны, вращение шкивов в одном направлении) являются требуемая (номинальная) мощность двигателя pном. И его частота вращения nдв = nном, тип ременной передачи.
Расчет открытой плоскоременной передачи
диаметр шкива электродвигателя обычно подбирают по заданному диаметру ведомого шкива.
диаметр ведущего шкива d1 определяется по формуле
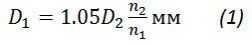
Где 1,05 - коэффициент скольжения ремня; d2 - диаметр ведомого шкива в мм; n1 и n2 - число оборотов соответственно ведущего и ведомого шкивов в минуту.
полученное значение d1 следует сопоставить с каталожными данными соответствующего электродвигателя. Диаметр шкива принимается равным или большим, чем указано в таблице. В отдельных случаях допускается уменьшение диаметра шкива против каталожных данных в пределах не более 10%.
длина ремня определяется по формуле
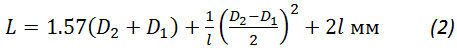
угол обхвата ремня в град. Подсчитывается по формуле
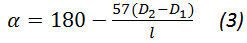
угол обхвата для плоских ремней должен быть не менее 150°. Если этот угол оказывается меньшим, то необходимо увеличить расстояние между центрами шкивов.
Расчет клиноременной передачи
при расчете клиноременной передачи определяют тип ремня, диаметры шкивов, длину и число ремней.
для расчета передачи должны быть известны:
Передаваемая мощность n в квт;
Число оборотов в минуту n1 и n2 соответственно ведущего и ведомого вала;
Ориентировочное межцентровое расстояние l0 в мм.
Применение большего числа ремней меньшего размера гарантирует более надежную работу передачи.
диаметры шкивов определяют из соотношения
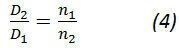
Где d2 и n2- соответственно расчетный диаметр и число оборотов большего шкива;
D1 и n1- соответственно расчетный диаметр и число оборотов меньшего шкива.
наружные и внутренние диаметры шкивов определяют по формулам
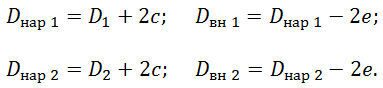 при расчете клиноременных передач определяют требуемое число ремней z в передаче для обеспечения среднего ресурса эксплуатации (2000ч). По гост 1284.3—80: при расчете клиноременных передач определяют требуемое число ремней z в передаче для обеспечения среднего ресурса эксплуатации (2000ч). По гост 1284.3—80:
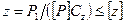 , ,
Где p1 - передаваемая мощность на ведущем валу, квт;
- коэффициент, учитывающий неравномерность распределения нагрузки между ремнями: при ; при ; при .
Для передач с клиновым ремнем рекомендуют из-за неодинаковой длины ремней и неравномерного поэтому их нагружения; для поликлиновых ремней (сечение к) (сечения л и м).
Рекомендуют применять поликлиновые ремни с четным числом клиньев.
Сила предварительного натяжения одного ремня без учета влияния центробежных сил (гост 1284.2—80):
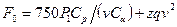 , ,
Где - мощность на ведущем валу передачи, квт; - скорость ремня, м/с; - число клиновых ремней в комплекте или число клиньев поликлинового ремня; - масса 1 м клинового ремня или одного клина поликлинового ремня, кг/м.
Средний ресурс , ч, ремней в эксплуатации при среднем режиме работы для классов ремней i, ii, iii и iv соответственно составляет: 2000, 2500, 2700 и 3700. С учетом режима работы и климатических условий ресурс вычисляют по формуле:
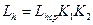 , ,
Где - коэффициент режима работы. Режим работы оценивают возможными кратковременными перегрузками: легкими – до 120% ( ), средний – до 150% ( ), тяжелый – до 200% ( ), очень тяжелый – до 300% ( ).
Коэффициент климатических условий эксплуатации для центральных и южных районов равен 1; для районов с холодным климатом – 0,75.
|
|
|
 Скачать 1.93 Mb.
Скачать 1.93 Mb.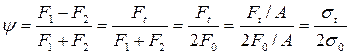 .
.

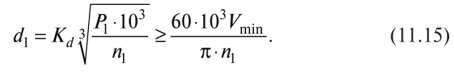
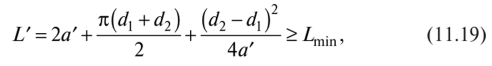
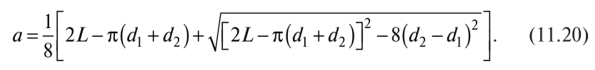
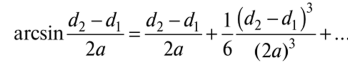
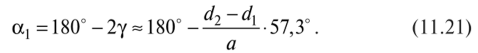




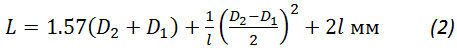
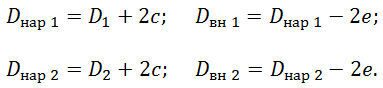 при расчете клиноременных передач определяют требуемое число ремней z в передаче для обеспечения среднего ресурса эксплуатации (2000ч). По гост 1284.3—80:
при расчете клиноременных передач определяют требуемое число ремней z в передаче для обеспечения среднего ресурса эксплуатации (2000ч). По гост 1284.3—80:



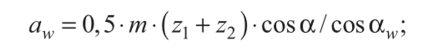
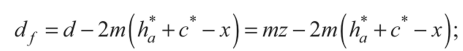
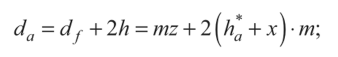
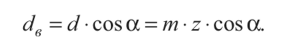 толщина зуба по делительной окружности
толщина зуба по делительной окружности