Шпоры по физхимии. 1 Энергия, теплота, работа. Первый зн термодинамики. Внутренняя энергия и энтальпия фи состояния системы
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
|
К зависит только от свойств чистого р-ля и характерна для данного р-ля. Физ.смысл К: она = понижению Т затвердевания одномоляльного р-ра. К – молек. понижение точки затвер-ния р-ра. Уравнение: 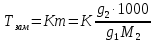 - возм-сть определить молек. вес М2 растворенного в-а по понижению т. затвердевания Т р-ра этого в-ва, содержащего g2 г его в 1000 г р-ля. - возм-сть определить молек. вес М2 растворенного в-а по понижению т. затвердевания Т р-ра этого в-ва, содержащего g2 г его в 1000 г р-ля.4.1. Некоторые т/x закономерности: применение теплот разрыва связей, Q образования и сгорания орг. соединений, Q нейтрализации, образования ионов, растворения и гидратации. Энергия хим. связи или теплота разрыва связи. Синтез к-л соед-я из исходных в-в сопряжен с затратой энергии на разрыв связи исходных в-в и обр-я связей в продукте р-ции: Н2С = СН2 + Н – Н → Н3С – СН3 Н – Н ΔН = 431,8 кДж С = С ΔН = 606,7 кДж С – С ΔН = -336,8 кДж 2(С – Н) ΔН = 821,7 кДж ΔНтеор = - 120 кДж ΔНпр = - 130 кДж Энергией связи м пользоваться для того, чтобы найти тепловой эф-т р-ции, если не известны теплоты обр-я в-в, участвующих в данной р-ции. Теплоты обр-я и сгорания орг. соед-ий. С6Н4(СООСН3)2 диметилфталлат Выписать теплоту обр-я бензола: С6Н6 ΔН = 82,8 кДж/моль Найти теплоту замещения одного Н: СН3 → Н ΔН = -18,8 кДж/моль Замещение в орто- пол-и: СН3 → Н ΔН = -24,4 кДж/моль Замещение водорода карбоксильной группы: 2СООН → 2СН3 ΔН = 2∙(-364) кДж/моль 2СН3 → 2СООН ΔН = 2∙39,7 кДж/моль Для орг-их в-в сущ-ют эмпирические закономерности. В ГОм ряду при добавлении каждой СН2-группы, теплота сгорания возрастает на 657 – 661 кДж. Теплоты нейтрализации. Если взять равное кол-во к-т и осн-ий и провести р-цию нейтрализации, то кол-во выделившейся теплоты независимо от вида сильных к-т и оснований одно и тоже -57,3 кДж. М+ + ОН- + Н+ + А- = М+ + А- + Н2О ΔН2980 = -57,3 кДж ОН- + Н+ = Н2О HCN + NaOH = NaCN + Н2О ΔH = 12,1 кДж остальное кол-во теплоты затрачивается на ионизацию CN- Н2 + ½ О2 → Н2ОЖ ↑ ↑ ОН-(aq), Н+(aq) Q2 = 285,06 – 57,3 = 227,76 кДж Н2 + ½ О2 + aq → ОН-(aq) + Н+(aq) ΔН2980 = -222.1176 кДж Теплота обр-я Н+ = 0 ΔH = -277,1176 кДж 4.2. Гетерогенные хим. равновесия. Вывод ур-ния для расчета константы равновесия. Гетерогенными хим. равновесиями наз. равновесные состояния для р-ий, участники кот. находятся в нескольких фазах. Примеры – равновесия реакций: FeO (т)+ CO = Fe (т) + CO2 (2 твердые и 1 газообразная фаза) Fe (ж)+H2S = FeS (р-р в Fe) + H2 (1 жидкая и 1 газообразная) Условие хим. равновесия ii = 0 сохраняет свое значение и для гетерогенного хим. равновесия. Исходя из него, найдем выражение для ЗДМ. Допустим, что в р-ии участвуют компоненты Аi газовой смеси с парц. Pi (летучестями fi ) и компоненты Bk р-ов (одного или нескольких жидких или твердых) с мольными долями Nk (активностями ak) : 1А1 + 2А2 + … + 1В1 + 2В2 + … = 1А1 + 2А2 + … + 1В1 + 2В2 + … разобьем сумму хим. потенциалов на две суммы – для газообразных участников (индекс i) и для компонентов жидких и твердых р-ов (индекс k): 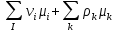 =0; i = Gi(T) + RT ln fi – для газов; =0; i = Gi(T) + RT ln fi – для газов; k = ko (T, P) + RT lnak – для жидких и тв. р-ов 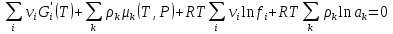 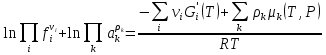 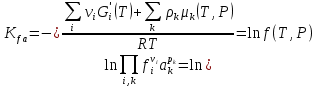 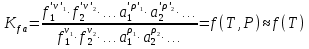 Это уравнение – наиболее общее выражение ЗДМ для хим. р-ий, протекающих м/у в-ми, находящимися в разных фазовых состояниях. Если газовая смесь есть ид. р-р ид. газов, где fi = Pi , а конденсированные фазы представляют собой также ид. р-ры, в кот. ak = Nk , то : 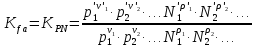 5. 1. Зависимость Q процесса от T (уравнения Кирхгофа, их вывод и анализ). Рассмотренные выше Q хим. р-ий являются Qи изотермических процессов и зависят от Т. QV = U = U2 U1 ; QP = H = H2 H1; Продифференцируем эти равенства по Т при V (P) = const : 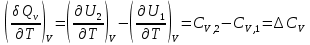 ; CV,2 мольная теплоемкость при V = const всей массы продуктов р-ии,CV,1 всей массы исходных в-в. ; CV,2 мольная теплоемкость при V = const всей массы продуктов р-ии,CV,1 всей массы исходных в-в. 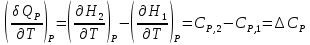 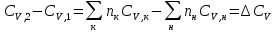 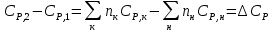 Уравнения Кирхгоффа дают зависимость Q хим. р-ии от Т. Дифференциальная форма записи уравнений : 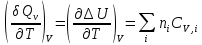 ; ; 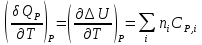 Для расчетов Q р-ий у-ния д. б. проинтегрированы : Для расчетов Q р-ий у-ния д. б. проинтегрированы :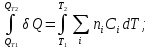 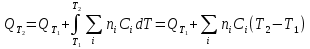 (Если интервал температур небольшой - десятки градусов то С от Т практически не зависит и 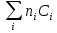 можно считать постоянной величиной). можно считать постоянной величиной).Если Т изменяется в широком интервале, то Сi const и для интегрирования надо знать зависимость С от Т. В широком интервале Т (не слишком низких выше 200 К) зависимости С чистых веществ от Т могут быть выражены эмпирическими степенными рядами : СР=a+bT+cT2+… (для орг. в-в); СР=a+bT+cT-2 (для неорг. в-в) СР=a+bT+cT-1/2 Интегральная форма записи уравнений Кирхгоффа : 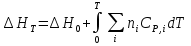 ; ; 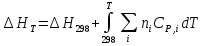 АДИАБАТИЧЕСКИЙ ПРОЦЕСС (Q = 0 , Q = 0) Это процесс, протекающий без теплообмена между системой и окр. средой. pdV + CV dT = 0; 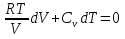 / : T ; / : T ;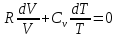 . . R = CP CV 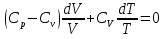 / : CV / : CV 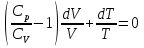 , , 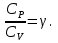 После интегрирования: ln V-1 + ln T = const; ln TV-1 = const => TV-1 = const; 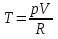 , , 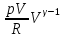 = const => PV = const уравненияадиабаты (уравненияПуассона). = const => PV = const уравненияадиабаты (уравненияПуассона).Работа в адиабатическом процессе: A + CV dT = 0 , A = CV dT , 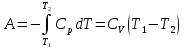 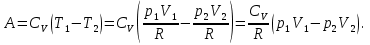 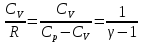 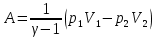 . .A 0 при расширении Т падает при адиабатическом расширении, т.е. работа адиабатического расширения совершается за счет уменьшения внутренней энергии. При адиабатическом сжатии U увеличивается, Т растет. Адиабата круче, чем изотерма. P V изотерма адиабата Термодинамика осмотического давления. Р-ль и р-р, разделенные полупроницаемой перегородкой и нах. в равновесии, представляют 2 фазы, один из компонентов, кот., свободно прох. из одной фазы в другую, должен иметь в обеих фазах равные хим. потенциалы. В чистом р-ле его хим. потенциал компонента 1о = const при Т, р1 = const (р1 – внешнее давление). В р-ре же его значение 1 изменяется с изменением N1 и р2 (р2 = р1 + – сумма первоначального P и дополнительного гидростатического P в р-ре, равного ). Это изменение можно найти, дифференцируя равенство 1 = 1о по N1 и р2 , учитывая, что d1o = 0. 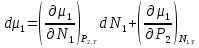 ; dP2 = d1o = 0; ; dP2 = d1o = 0;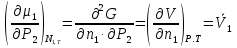 ; ( Т.к. ; ( Т.к. 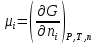 и и 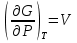 ); );  – обозначение частной производной по ni; 1 = 1o + RT ln a1 – обозначение частной производной по ni; 1 = 1o + RT ln a1 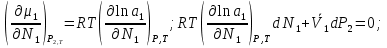 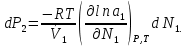 Интегрируем, считая Интегрируем, считая  const: const: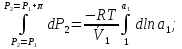 (пределы интегрирования: нижний – чистый р-ль, верхний – р-р) (пределы интегрирования: нижний – чистый р-ль, верхний – р-р)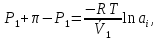 a1 = P1 / P1o ; P1 и P1o – давление насыщенного пара р-ля над р-ом и над чистым р-лем. a1 = P1 / P1o ; P1 и P1o – давление насыщенного пара р-ля над р-ом и над чистым р-лем. 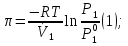 Для идеальных р-ов N1 = P1 / P1o (уравнение Рауля) и 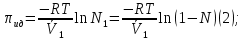 Для разбавленных р-ов (N 1): 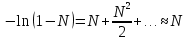 ; ; 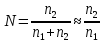 ; ; 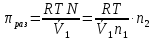 . .Если n2 n1 , то 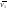 n1 = V (объему р-ра); n2 /V = c2 – моляльность. Получаем для разб. р-ов уравнение Вант-Гоффа: n1 = V (объему р-ра); n2 /V = c2 – моляльность. Получаем для разб. р-ов уравнение Вант-Гоффа: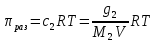 Т.о., это уравнение справедливо только для разбавленных р-ов, подчиняющихся з-ну Рауля. При повышении концентрации, даже если р-р подчиняется з-ну Рауля, т.е. идеален, уравнение Вант-Гоффа неприменимо и заменяется уравнением (2); в общем же случае неидеальных р-ов справедливо лишь уравнение (1). Энтальпия Н это сумма (U) и внешней (pV): H =U + pV . Q, передаваемое системе при p = const, расходуется на приращение энтальпии. H = U + pV. Изменение энтальпии в изобарном процессе включает в себя изменение U и PV, причем изменение U равно A изобарного расширения (сжатия). Н ф-ия состояния, т.к. ее изменение не зависит от пути процесса. Если процесс идет при P = const QP = dU + pdV = dU + d (pV) = d (U + pV) = dH Тепло, передаваемое системе при р=const, расходуется на приращение энтальпии. QP = dH , QP = H Если процесс изобарно-изотермический, то U = 0 и H = PV.  , dH = CP dT , H = CP T , dH = CP dT , H = CP TИзменение Н может быть во многих случаях легко измерено, вследствие чего эта ф-ия широко применяется при т/д исследованиях, особенно изобарных процессов. Абсолютное значение энтальпии не может быть вычислено. Изучение Т затвердевания р-ров называют криоскопией, а метод определения молекулярных весов – криоскопическим. Определение молекулярных весов криоскопическим методом является более точным, чем определение эбуллиоскопическим методом. Правильные результаты получаются при отсутствии диссоциации или ассоциации молекул растворенного в-ва в разбавленном р-ре. В случае ид. р-ов уравнение  можно использовать для определения Т затвер-ния р-ов любого состава. Это уравнение неприменимо для неид. р-ов. Применяя уравнение можно использовать для определения Т затвер-ния р-ов любого состава. Это уравнение неприменимо для неид. р-ов. Применяя уравнение  к р-лю и интегрируя его, можно из криоскопических данных вычислить активность р-ля в реальном р-ре. Один из точных методов вычисления активности. ЭБУЛЛИОСКОПИЯ (Повышение Т кипения растворов нелетучих веществ). Жидкость начинает кипеть, когда P ее насыщенного пара становится = внешнему P. Т.к. пар р-ра нелетучего в-ва содержит лишь чистый р-ль, то, в соответствии с з-ом Рауля, P насыщенного пара такого р-ра всегда меньше P насыщенного пара чистого р-ля при той же Т. АВ – зависимость P насыщенного пара чистого р-ля от Т; АВ, АВ – зависимость P насыщенного пара р-ов разной конц. от Т, N N. Видно : чем больше N (мольная доля растворенного в-ва в р-ре), тем больше Т = Т – То. Пусть р-р предельно разбавлен, так что он подчиняется з-ну Рауля. Найдем количественную зависимость Т от конц. р-а при P насыщенного пара, равном постоянному внешнему P: Р1 = Р1оN1 = Po = const.  Логарифмируем и дифференцируем это уравнение:  =0 (если Ро=1 атм.). В соотв. с уравнением Клапейрона-Клаузиуса: =0 (если Ро=1 атм.). В соотв. с уравнением Клапейрона-Клаузиуса: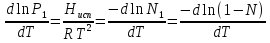 ; ;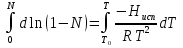 .Нисп=const в небольшом интервалеT. .Нисп=const в небольшом интервалеT.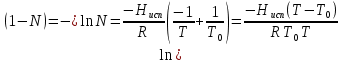 . Т.к. величина N достаточно мала, можно разложить lnв ряд и ограничиться первым членом разложения: . Т.к. величина N достаточно мала, можно разложить lnв ряд и ограничиться первым членом разложения: Т.к.Т мала, то То Т1 То2.Тогда Т.к.Т мала, то То Т1 То2.Тогда 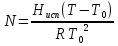 ; ;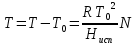 . .В разбавленных растворах  ; (М1 и М2 – молекул. веса компонентов, g1 и g2 – их весовые кол-ва в р-ре). Положим g1 = 1000 г, тогда g2/М2 = m – моляльность р-ра. ; (М1 и М2 – молекул. веса компонентов, g1 и g2 – их весовые кол-ва в р-ре). Положим g1 = 1000 г, тогда g2/М2 = m – моляльность р-ра. 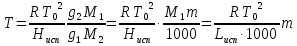 ; Lисп. = Нисп /М1 – уд. Q испарения р-ля. ; Lисп. = Нисп /М1 – уд. Q испарения р-ля.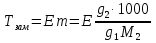 -Е – const, характерная для данного р-ля; не зависит от природы растворенного в-ва; наз. эбуллиоскопической постоянной. Физ. смысл Е : равна повышению Ткип одномоляльного р-ра; иначе Е наз. молекулярным повышением Т кипения. В действительности при m 1 уравнение перестает быть правильным из-за введенных математических упрощений и отклонений от з-на Рауля. -Е – const, характерная для данного р-ля; не зависит от природы растворенного в-ва; наз. эбуллиоскопической постоянной. Физ. смысл Е : равна повышению Ткип одномоляльного р-ра; иначе Е наз. молекулярным повышением Т кипения. В действительности при m 1 уравнение перестает быть правильным из-за введенных математических упрощений и отклонений от з-на Рауля.Приведенное уравнение дает возможность вычислять молекулярный вес растворенного в-ва М2, если известно Ткип р-ра определенной весовой конц. Метод определения М2 по уравнению наз. эбуллиоскопией (эбуллиометрией). Стандартная теплота сгорания (Hoc, 298) тепловой эффект р-ии взаимодействия 1 моля в-ва с кислородом с образованием при этом продуктов полного окисления при станд. условиях Тепловой эффект р-ии можно рассчитать по теплотам сгорания исх. и конечных в-в. Второе следствие из закона Гесса: Стандартная теплота хим. реакции равна разности стандартных теплот сгорания реагентов и продуктов реакции. |
