Шпоры по физхимии. 1 Энергия, теплота, работа. Первый зн термодинамики. Внутренняя энергия и энтальпия фи состояния системы
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
|
(Но298)x = n (Нoc, 298)нач.в-в n (Нoc, 298)конеч.в-в Теплоты сгорания часто используются для нахождения теплот р-ий органических соединений, кот. почти никогда не протекают однозначно и до конца. Это объясняется двумя причинами: 1) горение в кислороде является р-ей, общей для всех орг. в-в и идущей при соблюдении некоторых условий до конца, т.е. полностью и однозначно; 2) техника сожжения орг. в-в при V = const достигла высокого совершенства и позволяет определить теплоту сгорания с точностью до 0,02%. Комбинируя теплоты сгорания, можно вычислить Q любой хим. р-ии м/у орг. в-ми. Недостаток расчета теплот реакции по теплотам сгорания: уменьшение относительной точности получаемых результатов по сравнению с точностью исходных данных. Третье следствие из закона Гесса: энтальпия хим. реакции равна разности энергий разрываемых и образующихся хим. связей. Вследствие наличия логарифмической зависимости между Gо и КР все действия сложения и вычитания для Gо при комбинировании р-ий преобразуются в действия умножения и деления для величин КР. Пример: известны Gо (Т = 1396 К) для реакций:
(III) = (II) (I) ; GоIII = GоII 2GоI = 75550 4580 = 80130 кал КР(III) = 3,51012 Расчеты G и констант равновесия различных р-ий легко выполняются путем комбинирования G р-ий образования соединений из простых в-в. Стандартный изобарный потенциал любой хим. Р-ии равен алгебраической сумме Gо для р-ий образования всех участников р-ии. Стандартные изобарные потенциалы образования хим. соединений при Р = 1 атм и Т=298К(Gо298) сведены в таблицу. Для простых в-в в их обычных состояниях Gо298 = 0. Очень часто тв., а иногда и жидкие фазы, участвующие в р-ии, являются практически чистыми индивид. соед-ми, активность и хим. потенциал кот. зависят только от Т. При Т = const ak = const, Nk = 1 и эти величины м. б. включены в константу равновесия. Если так обстоит дело для всех конденсированных фаз, участвующих в р-ии, то уравнения ЗДМ включают только летучести (Pi) газообразных участников р-ии. Так, для реакции FeO (т) + H2 = Fe (т) + H2O (г) при высоких Т: 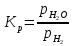 Гетерогенная реакция получения генераторного газа С + СО2=2СО имеет важнейшее техническое значение. Равновесие этой реакции определяет состав газов в процессах горения при недостатке О2. 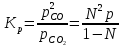 Теплоты растворения и гидратации. При раст-и тв крист в-ва тратится энергия на разрушение крист рещ, и одновременно выделяется энергия при вз-и образовавшихся ионов с р-лем. Соотношение затраченной и выделенной энергии опр-ет тепловой эф-т раст-я. Кол-во выд-ой или поглощ-ой теплоты зависит от конц-и полученного р-ра. Интегральная Q раст-я – изменение энтальпии в процессе раст-я 1 моль в-ва в n моль р-ля. Дифференциальная теплота - теплота раст-я 1 моль в-ва в очень большом кол-ве р-ра нек-ой постоянной конц-и. Теплота рас-я 1 моль р-ля наз теплотой разбавления. HClг + 5Н2ОЖ = НСl ΔH = -64 кДж ΔH = -75,1 кДж предельная величина Это дает возможность рассчитать теплоту разбавления 195 моль Н2О в НСl в 5 Н2О HClг + 200Н2ОЖ = НСl в 200 Н2О HCl + 5Н2О + 195Н2О = Используя з-н Гесса, м рассчитать теплоту гидратации 5. 2. Диаграммы состояния двухкомпонентных систем с ограниченной растворимостью компонентов в тв. состоянии (2 случая). Тв. р-ы (смешанные кристаллы) однородные системы переменного состава (как и жидкие р-ы), т.е. тв. фаза не представляет собой кристаллов чистого компонента или хим. соединения, а состоит из 2x или более компонентов, одновременно участвующих в образовании кристаллов и равномерно распределяющихся в нем. Области на диаграмме см. подписи на рис. -твердый р-р В в А -твердый р-р А в В Рассмотрим равновесные состояния, через кторые проходят при охлаждении 2 различных расплава. 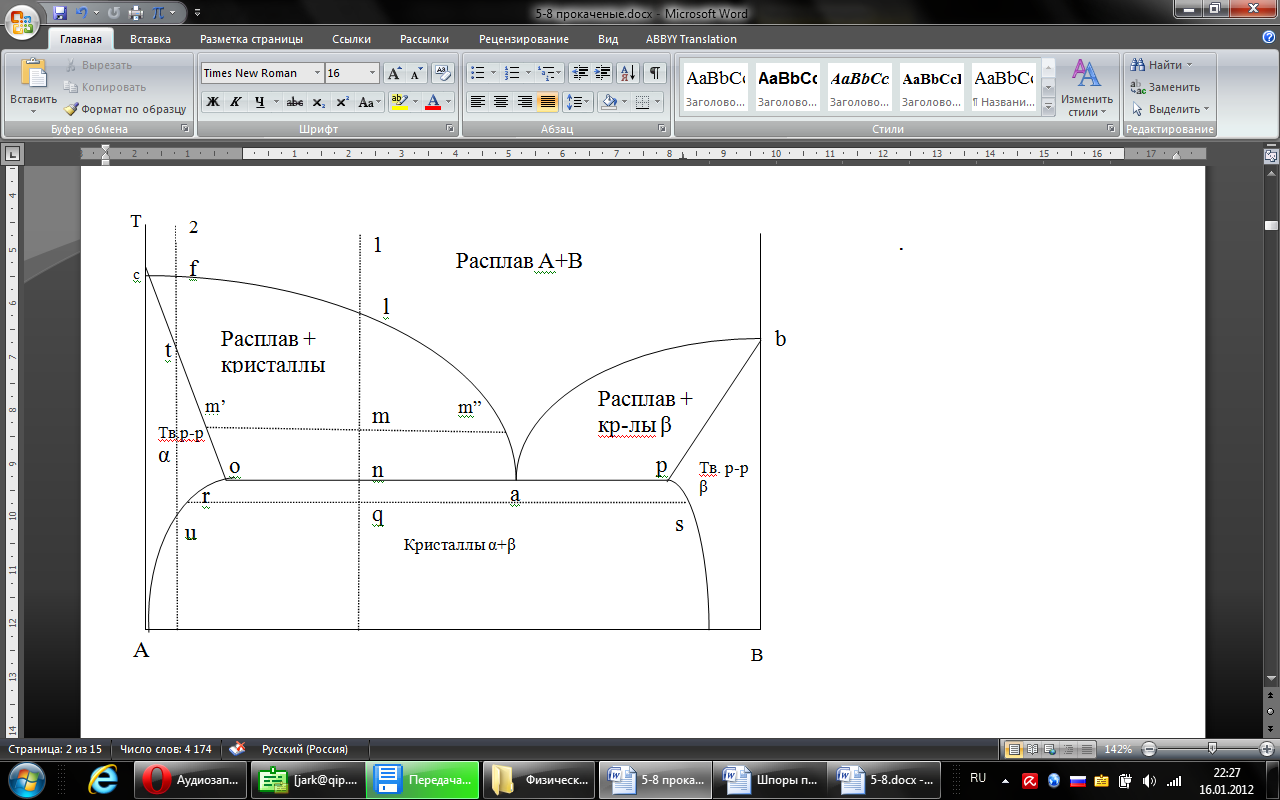 6. 1. Обратимые и необратимые, самопроизвольные и не самопроизвольные процессы. Обратимый цикл Карно. Формулировки 2-го закона термодинамики. Равновесный процесс проходит в прямом и обратном направлении через одни и те же состояния, бесконечно близкие к равновесию. A равновесного процесса имеет макс. величину по сравнению с неравновесными процессами и наз-ся максимальной работой. Если равновесный процесс протекает в прямом, а затем в обратном направлении так, что не только система, но и окр. среда возвращается в исх. состояние и в результате процесса не остается никаких изменений во всех участвовавших в процессе телах, то процесс наз-ся обратимым. Пример равновесных процессов ид. механические процессы, протекающие без трения. Примеры крайних случаев неравновесных процессов : переход Q от тела с большей Т к телу с меньшей Т; переход механической A в Qпри трении; расширение газов в пустоту. Все неравновесные процессы протекают в направлении достижения равновесия и протекают «сами собой», т.е. без воздействия внешней силы. Процессы, протекающие сами собой и приближающие сис-му к равновесию, являются самопроизвольными (+). Процессы, не могущие протекать сами собой, без воздействия извне, удаляющие систему от равновесия несамопроизвольные (-). В изолированной системе, где исключены внешние воздействия, могут протекать только самопр-ные процессы. В машинах, производящих A (тепловых машинах), определенное кол-во к-л в-ва, называемое рабочим телом, совершает цикл-ую последовательность процессов, периодически возвращаясь в исх. состояние. Таким путем достигается превращение Q в A. Важнейший – цикл Карно. 1)Изотермическое расширение при Т = Т1 : газ находится в контакте с нагревателем с Т1 , получает Q1, совершает А1: 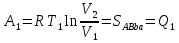 2)Адиабатическое расширение : Т1 падает до Т2: A2=CV(T1T2)=SBCcb 2)Адиабатическое расширение : Т1 падает до Т2: A2=CV(T1T2)=SBCcb3)Изотермическое сжатие при Т = Т2 : газ находится в контакте с холодильником с Т2 , которому отдает Q2: 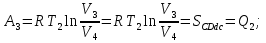 4)Адиабатическое сжатие : А4=CV(Т2Т1)=CV(Т1Т2)=SDAad 4)Адиабатическое сжатие : А4=CV(Т2Т1)=CV(Т1Т2)=SDAad 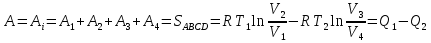 ;A0Q1Q20Q1Q2 ;A0Q1Q20Q1Q2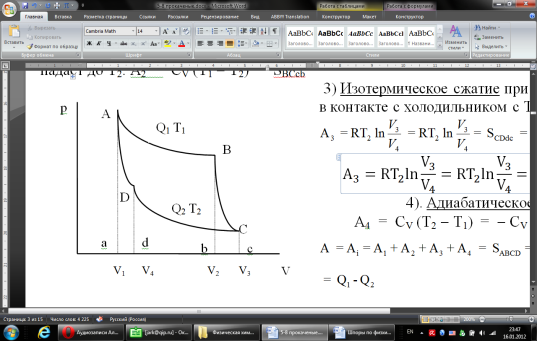 U ид.газа не изменилась. A, произведенная газом, совершена за счет Q1 ,поглощенной системой от некоторого источника тепла с постоянной Т1 (нагреватель). Однако только часть Q превращается в A другая часть Q2 передана газом внешней среде некоторому телу с постоянной Т2 (холодильник). 6.2. Диа-мы равновесия жидкость-пар. 1 и 2 з-ны Коновалова. Фрак-ная перегонка. 1. Т = const, Диаграмма равновесия бинарный раствор – пар. 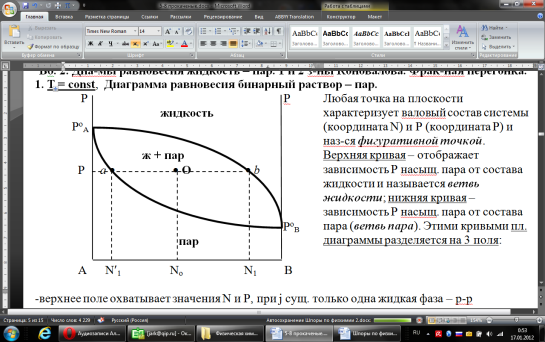 Любая точка на плоскости характеризует валовый состав системы (координата N) и P (координата Р) и наз-ся фигуративной точкой. Верхняя кривая – отображает зависимость P насыщ. пара от состава жидкости и называется ветвь жидкости; Нижняя кривая – зависимость P насыщ. пара от состава пара (ветвь пара). Этими кривыми пл. диаграммы разделяется на 3 поля: 1)Верхнее поле охватывает значения N и P, при j сущ. только одна жидкая фаза – р-р переменного состава. 2)Нижнее – газовая смесь переменного состава. В этих полях любая точка изображает состояние однофазной системы. 3)Среднее поле соответствует двухфазной системе р-р + насыщ.пар. Рассмотрим точку О. Точка, а характеризует состав насыщ. пара; точка b характеризует состав р-а. 2. Р = const, Диаграмма Т кипения – состав раствора. Эта диаграмма имеет зеркально-подобный вид по отношению к диаграмме P – N, но подобие – качественное. Верхняя кривая – ветвь пара, нижняя – ветвь жидкости. Проследим ход перегонки р-ра 2x жидкостей. Nо – смесь исх. состава; нагреваем при постоянном вн. P до кипения (кипение начнется при Т = t1 ; точка а1). Первые порции пара (им отвечает точка b1) имеют состав N1. В процессе испарения (Т повысилась до t2) изменится состав жидкости (точка а2) и состав пара (точка b2); конденсация этого пара даст жидкую фракцию состава N2. При дальнейшем испарении составы жидкости и пара снова изменятся и т.д. Составы жидкости будут изменяться по ветви жидкости до т. а3, составы пара – по ветви пара до т. b3, где состав пара станет равенNо. Кипение закончится при Т = t3; последняя капля жидкости будет иметь состав N3. 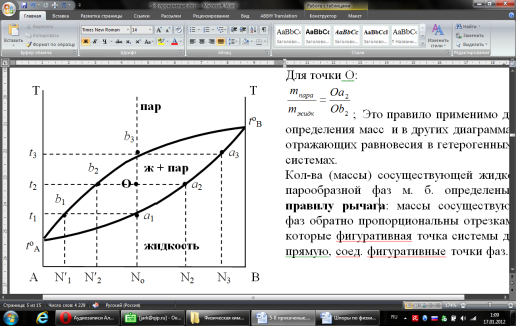 Для точки О: 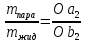 ; Это правило применимо для определения масс и в других диаграммах, отражающих равновесия в гетерогенных системах. ; Это правило применимо для определения масс и в других диаграммах, отражающих равновесия в гетерогенных системах.Кол-ва (массы) сосуществующей жидкой и парообразной фаз м. б. определены по правилу рычага: массы сосуществующих фаз обратно пропорциональны отрезкам, на которые фигуративная точка системы делит прямую, соед. фигуративные точки фаз. 7. 1. Энтропия в случае равновесных и неравновесных процессов. Изменение S изолированной системы и направление процесса. У-ия равновесия в изолиров. системе. Если интеграл по замкнутому контуру = 0, то имеется такая ф-ия от переменных интегрирования, полный дифференциал которой равен подынтегральному выражению, т.е. имеется ф-ия S, для которой: 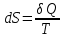 Эта функция энтропия S. Интеграл по замкнутому контуру можно разбить на два интеграла : Эта функция энтропия S. Интеграл по замкнутому контуру можно разбить на два интеграла :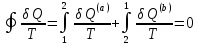 ; ; 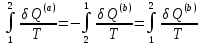 Т.о., сумма приведенных Q (интеграл элементарных приведенных Q) при переходе системы равновесным путем из состояния 1 в состояние 2 не зависит от пути процесса, а только от начального (1) и конечного (2) состояний. => интеграл элементарных приведенных Q в равновесном процессе = приросту некоторой ф-ии состояния системы : 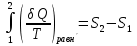 , , 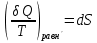 Энтропия есть ф-ия сост. системы: ее изменение равно сумме приведенных Q, поглощ-ных сист. в равновес. процессе. Энтропия есть ф-ия сост. системы: ее изменение равно сумме приведенных Q, поглощ-ных сист. в равновес. процессе.Она - однозначной, непрер. и конечной ф-ей состояния. S (как и теплоемкость) : Дж/(Кмоль) или Дж/(Кг) (кал/(Кмоль) или кал/(Кг)) 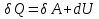 / : T и все это равно dS. / : T и все это равно dS.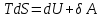 ; ; 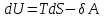 ; ; 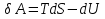 Эти равенства охватывают уравнения I и II ЗТ ; они справедливы лишь для равновесных процессов. Эти равенства охватывают уравнения I и II ЗТ ; они справедливы лишь для равновесных процессов.Энтропия в случае неравновесных процессов. 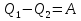 ; А в необратимом цикле меньше, чем в обратимом ; А в необратимом цикле меньше, чем в обратимом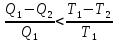 ; ; 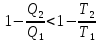 ; ; 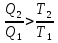 ; ; 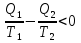 . Для б/м цикла Карно 1-го вида: . Для б/м цикла Карно 1-го вида: 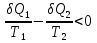 ; ; 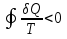 неравенство Клаузиуса. неравенство Клаузиуса. Пусть в цикле переход (а) (1 2) равновесен, переход (b) (21)не равновесен (круговой процесс в целом - не равновесен): 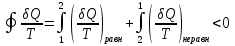 ; ; 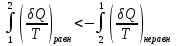 ; ;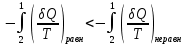 (поскольку переход (а) равновесен, пределы интегрирования можно поменять местами) (поскольку переход (а) равновесен, пределы интегрирования можно поменять местами)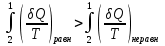 ; ; 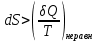 В общем случае: В общем случае: 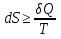 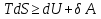 ; ; 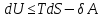 ; ; 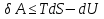 охватывают уравнения I и II ЗТ ; они справедливы и для равновесных, и для неравновесных процессов. охватывают уравнения I и II ЗТ ; они справедливы и для равновесных, и для неравновесных процессов.Если система изолированная ( 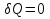 ), то ), то 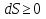 : :
7.2. Примеры хим. равновесий в некоторых идеальных газовых смесях. Р-ции, протекающие в газовой фазе без изменения числа м-л Р-ции, в результате к-ых число м-л не меняется, принадлежат к простейшему стехиометрическому типу р-ций. К этому типу относятся: получения водяного газа CO + H2O CO2 + H2 синтеза окиси азота N2 +O 2 2NO Одной из первых р-ий такого типа, равновесие которых было изучено, является р-ия синтеза HJ (Боденштейн): 1/2H2 + 1/2J2 HJ 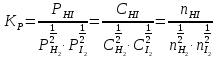 ( рi = (ni/V) RT = ci RT ; множители RT/V или RT сокращаются, т.к. число молекул или объем смеси в результате реакции не изменяются); КР = КС = КN . Обозначим: а нач. число молей Н2, b нач. число молей J2, х число молей образовавшегося HJ. Тогда числа молей в равновесной смеси будут равны : ( рi = (ni/V) RT = ci RT ; множители RT/V или RT сокращаются, т.к. число молекул или объем смеси в результате реакции не изменяются); КР = КС = КN . Обозначим: а нач. число молей Н2, b нач. число молей J2, х число молей образовавшегося HJ. Тогда числа молей в равновесной смеси будут равны :nHJ = x, nH2 = a 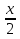 , nI2= b , nI2= b 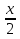 Подставим эти значения в уравнение: Подставим эти значения в уравнение: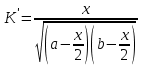 Решение этого урав: Решение этого урав: 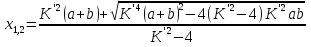 Зная К, а, b , можно вычислить х и сравнить с опытными величинами. Рассмотрим теперь реакцию термической диссоциации HJ, обратную разобранной: HJ 1/2H2+1/2J2 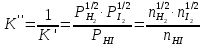 Как и для всякой р-ии диссоциации, константа равновесия может быть выражена через степень диссоциации , являющуюся долей продиссоциировавших молекул от общего числа молекул no . При равновесии : 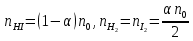 , , 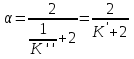 Если в исходной смеси, кроме HJ, находится один из продуктов реакции, то принимает иное, меньшее значение. От общего давления степень диссоциации HJ не зависит, и при сжатии равновесной смеси ее состав не изменится. и К (константа диссоциации) явл. количественными характеристиками прочности соед-ия и у разных в-в они, естественно, различны (при одинаковых условиях). Реакции, протекающие в газовой фазе с изменением числа молекул Наиболее простыми из таких реакций являются реакции диссоциации одной молекулы на две одинаковые или разные молекулы (или атомы). К ним относятся : диссоциация молекулярного J2 (Br2, Cl2, N2, O2 ...) : J2J +J N2O4 2NO2 PCl5 PCl3+Cl2 и т.д. Рассмотрим р-ию диссоциации N2O4 (при Т, близких к комнатной): 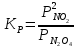 Выразим КР через степень диссоциации N2O4. Обозначим : no исходное число молей N2O4. При равновесии : 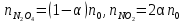 Общее число молей в смеси n = no no + 2 no = no + no = (1 + ) no Тогда парциальные давления будут равны (Р общее давление) : 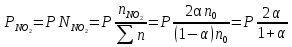 , , 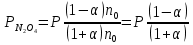 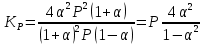 |

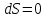 , S=const энтропия изолированной системы постоянна, если в ней протекают равновесные процессы.
, S=const энтропия изолированной системы постоянна, если в ней протекают равновесные процессы.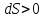 ,
, 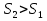 , S растет.
, S растет.