Шпоры по физхимии. 1 Энергия, теплота, работа. Первый зн термодинамики. Внутренняя энергия и энтальпия фи состояния системы
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
|
13.2. Гетерог. равновесия. Составл. в-ва системы, комп-ты, фазы, степ. свободы. Правило фаз. Равновесие гетерог. систем означает рав-во каждого компонента во всех фазах, а также min значение одного из термодинам. пот-лов или max значение S всей системы при соотв. условиях. Фаза – совокуп. всех гомоген. частей системы, одинаковых во всех точках по составу и всем хим. и физ. св-вам и отгранич. от др. частей видимой пов-тью раздела. Пов-ти раздела фаз образ. некоторым кол-вом молекул; молекулы, образ. поверхн. слой, находятся в особ. условиях, поэтому поверх. слой облад. св-вами, не присущими в-ву, находящемуся в глубине фазы (н-р, избыточной U). Образования, составленные из небол. числа молекул, не м.б. разделены на поверхностный слой и внутр. массу в-ва. Поэтому к образованиям с очень малым V понятие «фаза» не подходит. Мелкие образования, в кот-х можно выделить поверхн. слой, явл. системами с очень развитой поверх-тью, и св-ва таких систем зависят от св-в и р-ров поверхностей раздела. Составляющее в-во системы - каждое в-во, которое м.б. выделено из системы и существовать вне ее. Н-р: в водн. р-ре NaCl составл. в-ва Н2О и NaCl; Na+ и Cl- не явл. составл. в-вами. Кол-во каждого из составл. в-в, вх. в систему, в кот-й отсут. хим. реакции, не зависит от кол-ва других в-в. Состав фаз равновес. системы в этом случае определяется конц-ми всех составл. в-в. Если протекают хим. реакции, то кол-ва составл. в-в, вх. в равновес. систему, зав. друг от друга, и состав фаз можно определить, зная конц. лишь части составляющих в-в. Компоненты системы (независимые составляющие в-ва) – составл. в-ва, конц. кот-х определяют состав фаз данной равновесной системы. Св-ва системы определяются не тем, какие в-ва выбраны в качестве компонентов, а числом компонентов. Правило фаз Гиббса : Число компонентов=числу составл. в-в системы - число уравнений, связывающих конц. этих в-в в равновес. системе (т.е число компонентов – это наим. число составл. в-в, достаточное для определения состава любой фазы системы.
14.1.Фаз. переходы I рода для индив. в-в. Урав. Клапейрона-Клаузиуса. Фаз. переходы II рода. Фаз. переходы (т.е. превращения агрегатных состояний) возможны в системе, сост. из неск. фаз чистого в-ва, наход. в равновесии. Рассм. равновесный переход 1 моля в-ва из фазы 1 в фазу 2 при Р,Т = const (жидкость – газ).U2–U1=Q–A=T(S2–S1)–P(V2–V1) (только А расширения) U2–TS2+PV2=U1–TS1+PV1; G2=G1. Изобар. пот-лы единицы m чистого в-ва в 2х фазах, нах-ся в равновесии, равны м/у собой. Для полных дифф-лов: dG1=V1dP–S1dT , dG2=V2dP–S2dT; dG2– G1=(V2–V1)dP–(S2–S1)dT=0 (= 0, т.к. сохран. фазовое равновесие и dG1 = dG2). 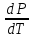 = = 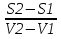 Т.к. процес равновесн. и изотерм., то можно записать: S2–S1=Q/T=Н/T ;Q–Q, поглощ. при переходе 1 моля в-ва из одной фазы в др; Н – теплота фазового превращения; Т – Т фазового превращения; V2 – V1 – р-ть мольных объемов 2х фаз. Т.к. процес равновесн. и изотерм., то можно записать: S2–S1=Q/T=Н/T ;Q–Q, поглощ. при переходе 1 моля в-ва из одной фазы в др; Н – теплота фазового превращения; Т – Т фазового превращения; V2 – V1 – р-ть мольных объемов 2х фаз. 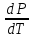 = =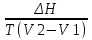 , ,Н = Т 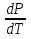 (V2 – V1) - урав. Клапейрона-Клаузиуса –общее термодинам. уравн, подходит ко всем превращениям агрегатных состояний чистых в-в. (V2 – V1) - урав. Клапейрона-Клаузиуса –общее термодинам. уравн, подходит ко всем превращениям агрегатных состояний чистых в-в. Фаз. Переходы I рода – фаз. переходы, характериз-ся равенством изобарн. потенциалов 2х сосуществующих в равновесии фаз и скачкообразным изменением S и V при переходе в-ва из одной фазы в др. (плавление, испарение, возгонка, переход из одной кристалл. модификации в др.). Плавление. 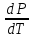 = = 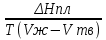 ; Нпл всегда 0; Vж Vтв для большинства в-в, т.е. плотность тв. фазы > плотн. жидкой. След-но, ; Нпл всегда 0; Vж Vтв для большинства в-в, т.е. плотность тв. фазы > плотн. жидкой. След-но, 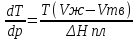 = 0 и с ростом Р температура плавл. повыш-ся. = 0 и с ростом Р температура плавл. повыш-ся. Испарение (возгонка). 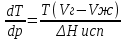 = 0 ; (Нисп всегда 0; Vг Vж для всех в-в, и поэтому Ткип всегда ↑ с ростом Т). Если Т далека от крит., Vг Vж, то Vж можно пренебречь. = 0 ; (Нисп всегда 0; Vг Vж для всех в-в, и поэтому Ткип всегда ↑ с ростом Т). Если Т далека от крит., Vг Vж, то Vж можно пренебречь.Нисп = Т 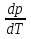 Vг. Если нас. пар можно считать ид. газом, то Нисп = Т Vг. Если нас. пар можно считать ид. газом, то Нисп = Т 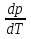 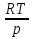 , , 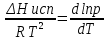 U = QV и H = QP справедливы, если в 1-м случае А = 0, а во 2-м соверш. только А расширения (А = 0). Поэтому в (1) и (3) 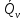 и и 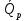 относ. не к процессам, которым соответствуют А или А, а к процессам, протекающим м/у теми же нач. и кон. состояниями, но без совер. работы (для QV) или с совер. только А расширения (для QP), т.е. в неравновесных условиях. Теплоты же равновесного процесса, равные ТS, выраж. послед. членами уравнений (1) и (3). Уравнения можно записать так: относ. не к процессам, которым соответствуют А или А, а к процессам, протекающим м/у теми же нач. и кон. состояниями, но без совер. работы (для QV) или с совер. только А расширения (для QP), т.е. в неравновесных условиях. Теплоты же равновесного процесса, равные ТS, выраж. послед. членами уравнений (1) и (3). Уравнения можно записать так:– F = Amax = – QV, неравн + QV, равн ; – G = Amax = – QP, неравн + QP, равн Обе модификации плавятся в точках Х и Y; Р пара модификации I во всей области существования кристаллов выше Р пара модификации II, =>, самопроизвольные превращения возможны лишь в направлении I II, н-р, после того как из жидкой фазы, переохлажденной до Т1, выделится модификация I. p O Y X I A B II T T1 Точка пересечения О не м. б. получена экспериментально. Она находится графически путем продолжения опытных кривых АХ и ВY. Взаимные превращения кристаллических фаз, j могут протекать самопроизвольно лишь в одном направлении, называются монотропными. Другой пример диаграммы, описывающей реальную монотропную систему, диаграмма состояния фосфора. 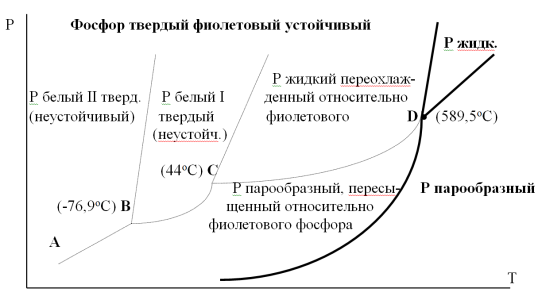 Пунктиром обозначены кривые давления паров неустойчивых фаз. Т. D соответствует устойчивому сосуществованию жидкого фосфора, твердого фиолетового фосфора и парообразного фосфора. Точки В и С соответствуют неустойчивому сосуществованию трех фаз : т. В двух модификаций белого фосфора и пара, т. С белого фосфора I, переохлажденного жидкого фосфора и пара. Диаграмма состояния фосфора пример системы, в которой могут происходить как монотропные превращения (фосфора белого I в фосфор фиолетовый), так и энантиотропные превращения (фосфора белого I в фосфор белый II, хотя оба они и являются неустойчивыми модификациями по сравнению с фиолетовым фосфором). U = U (S,V) ; dU = 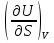 dS + dS + 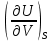 dV ; dV ; 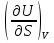 = T , = T , 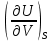 = – P. = – P.Т – мера приращения U с ростом S при V = const; Р – мера убыли U с ростом V при S = const. При S,V = const: (U)S,V 0 При всех неравн-ных изохорно-изэнтропных процессах U убывает; когда U достигает мин., система приходит в равн-ие. (U)S,V 0 – критерий напр. протекания процесса при S,V = const; (U)S,V = 0 , ( 2U)S,V 0 – условие равновесия. U – изохорно-изэнтропный термодинамический потенциал. H= U + PV;dH = dU + PdV + VdP , dU TdS – PdV; dH TdS + VdP , H = H (S,P); dH = 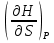 dS + dS + 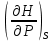 dP; dP; 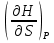 = T , = T , 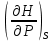 = V;Т – мера приращения Н с ростом S при P = const; V – мера приращения H с р-м P при S = const. = V;Т – мера приращения Н с ростом S при P = const; V – мера приращения H с р-м P при S = const.При S,P = const: (H)S,P 0; (H)S,P 0 – критерий направления процесса в условиях S,P = const;(H)S,P = 0 , ( 2H)S,P 0 – критерий достижения равновесия. Н – изобарно-изэнтропный потенциал. U, Н – эти ф-ии могут служить критерием равновесия при S = const. S непосредственно измерить нельзя, и контроль ее постоянства при неравновесных процессах затруднителен. Поэтому функции U и Н не находят широкого применения в качестве критериев направления процесса и равновесия. dU = TdS – PdV; dH = TdS + VdP; dF = – SdT – PdV; dG = – SdT + VdP выражения образуют замкнутую группу, в которой 2 пары переменных – Т и S (параметры, связанные с Q) и Р и V (параметры, связанные с A) дают все возможные сочетания. В зависимости от характера изучаемого процесса может быть использована та или иная из этих функций. Важное свойство этих ф-ий: через каждую из этих ф-ий и ее производные можно выразить в явной форме любое т/д свойство сист.. Каждая ф-я дает, т.о., полную т/д харак-ку сист.. Поэтому эти ф-ии наз. характеристическими ф-ми. Каждая ф-ия обладает свойствами характ-кой ф-ии только при соответствующем, характерном для нее наборе независимых переменных. (незвисимые переменные – естественные переменные) Энтропию также можно отнести к этим функциям Q=dU+ATdS , TdSdU+PdV , S=S(U,V) (S)U,V0–критерий самопроизвольного протекания проц. в условиях U,V=const; (S)U,V = 0 , ( 2S)U,V 0 – критерий равновесия. Т.о., условия равновесия системы можно сформулировать следующим образом: в состоянии равновесия системы ее термодинамические потенциалы имеют минимальное значение при постоянстве своих естественных переменных, а энтропия имеет максимальное значение. Другое общее свойство термодинамических потенциалов – то, что убыль их в равновесном процессе при постоянстве естественных переменных равна максимальной полезной А. Термодинамика осмотического давления. Р-ль и р-р, разделенные полупроницаемой перегородкой и нах. в равновесии, представляют 2 фазы, один из компонентов, кот., свободно прох. из одной фазы в другую, должен иметь в обеих фазах равные хим. потенциалы. В чистом р-ле его хим. потенциал компонента 1о = const при Т, р1 = const (р1 – внешнее давление). В р-ре же его значение 1 изменяется с изменением N1 и р2 (р2 = р1 + – сумма первоначального P и дополнительного гидростатического P в р-ре, равного ). Это изменение можно найти, дифференцируя равенство 1 = 1о по N1 и р2 , учитывая, что d1o = 0. 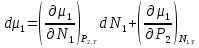 ; dP2 = d1o = 0; ; dP2 = d1o = 0;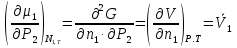 ; ( Т.к. ; ( Т.к. 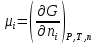 и и 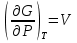 ); );  – обозначение частной производной по ni; 1 = 1o + RT ln a1 – обозначение частной производной по ni; 1 = 1o + RT ln a1 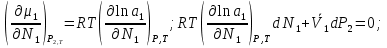 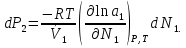 Интегрируем, считая Интегрируем, считая  const: const: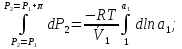 (пределы интегрирования: нижний – чистый р-ль, верхний – р-р) (пределы интегрирования: нижний – чистый р-ль, верхний – р-р)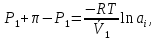 a1 = P1 / P1o ; P1 и P1o – давление насыщенного пара р-ля над р-ом и над чистым р-лем. a1 = P1 / P1o ; P1 и P1o – давление насыщенного пара р-ля над р-ом и над чистым р-лем. 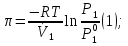 Для идеальных р-ов N1 = P1 / P1o (уравнение Рауля) и 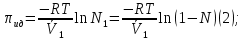 Для разбавленных р-ов (N 1): 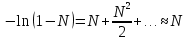 ; ; 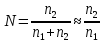 ; ; 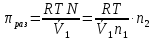 . .Если n2 n1 , то 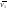 n1 = V (объему р-ра); n2 /V = c2 – моляльность. Получаем для разб. р-ов уравнение Вант-Гоффа: n1 = V (объему р-ра); n2 /V = c2 – моляльность. Получаем для разб. р-ов уравнение Вант-Гоффа: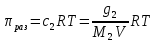 Т.о., это уравнение справедливо только для разбавленных р-ов, подчиняющихся з-ну Рауля. При повышении концентрации, даже если р-р подчиняется з-ну Рауля, т.е. идеален, уравнение Вант-Гоффа неприменимо и заменяется уравнением (2); в общем же случае неидеальных р-ов справедливо лишь уравнение (1). Если равновес. система с вероятностью W и энтропией S состоит из 2х частей с вероятн. W1 и W2 и энтропиями S1 и S2 , то можно записать: S1=f(W1) , S2=f(W2); S=f(W)=f(W1W2) , S1+S2=f(W1)+f(W2); f(W)=f(W1W2)=f(W1)+f(W2). Для системы из многих частей: f(W)=f(W1W2…Wk)= =f(W1)+f(W2)+…+f(Wk). Решением явл. урав-е Больцмана: S = k ln W, k–пост. Больцмана; k=R/NA.  Рассм. –ц- изотерм. расшир. 1 кмоля ид. газа. Рассм. –ц- изотерм. расшир. 1 кмоля ид. газа.S= 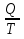 = =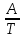 =Rln =Rln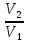 =kNln =kNln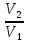 ; ;W1= 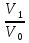 –вероятн. нахождения 1 молекулы в V1; W1= –вероятн. нахождения 1 молекулы в V1; W1=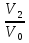 –вероятн. нахождения 1 молекулы в V2; –вероятн. нахождения 1 молекулы в V2;Для N молекул: WN = 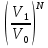 , WN = , WN = 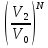 ; ;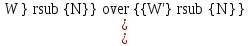 = = 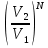 , ln , ln 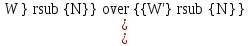 = N ln = N ln 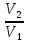 , S = k ln , S = k ln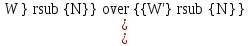 S2–S1=klnWN–klnWN , S=klnW+const, сonst = 0 – постулат Больцмана S = k ln W . Это соотношение вскрывает статист. хар-р II з. термод.. Условие возрастания S в изолир. системе не обязательно, а вероятно. Возможны самопроизвольные отриц. процессы, сопровождающиеся уменьш. S в изолир. системе, н-р, флуктуации плотности. Знач. отклонения от сред. величин в больших системах имеют исчезающе малую вероятность, но они также возможны. Установление статист. хар-ра II з. термод. явл. заслугой Больцмана, объяснившего т.о. противоречие м/у обратимостью механич. движения и необратимостью и направленностью реал. физ. и хим. процессов. Эта направленность явл. следствием молекуляр. строения материального мира. В работах Больцмана показан статист. хар-р II з. термод. и кол-венно изучены отклонения закона, показана несостоятельность идеи тепл. смерти вселенной (Клаузиус). 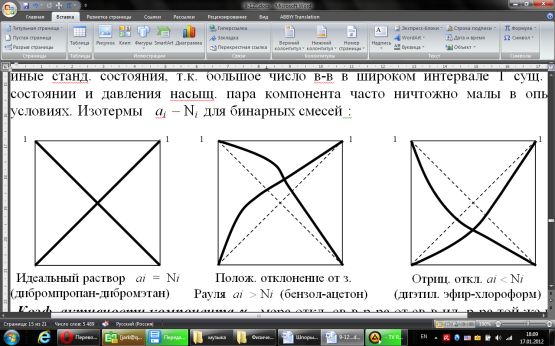 Коэф. активности компонента i - мера откл. св-в р-ра от св-в ид. р-ра той же конц. i = 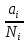 = = 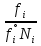 = = 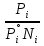 Для ид. р-ров i = 1 ; в случ. полож. отклонений РiPioNi и i1 ; в случ. отриц. отклонений Рi PioNi и i 1. В предельно разбав. р-рах коэфф-ты активности р-ля и раств. в-в равны 1, если прав. выбраны станд. состояния. Возможно сопоставление акт-ей компонентов с конц., выраж. не только в Ni: | ||||||
