Шпоры по физхимии. 1 Энергия, теплота, работа. Первый зн термодинамики. Внутренняя энергия и энтальпия фи состояния системы
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
|
16.2. Влияние Т на хим. равновесие. Уравн. изохоры и изобары –ц-, их вывод, анализ, интегр-е. В соответствии с принципом подвижного равновесия можно установить кач-венное правило смещения хим. равновесия с изм. Т. При ↑ температуры Т смещение равновесия должно сопровождаться увелич. S; т.к. (Т)Р (S)Т 0, то хим. равновесие при ↑ Т должно сместиться в сторону эндотерм. реакции, а при ↓ Т – в том направлении, в кот-м протекает экзотерм. реакция. Выражение для кол-венной зав-ти хим. равновесия от Т можно получить из 2х ур.: 1) Урав. изотермы реакции Вант-Гоффа для изобар. потенциала хим. реакции: G= –RTlnKP+RTilnPi(1) (Pi–исход. парц. Р; постоянны) 2) Уравн. max работы Гиббса-Гельмгольца : G=H+T 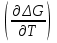 p (2) p (2)Подставим (1) в 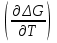 p : p : 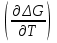 p= –RlnKP–RT p= –RlnKP–RT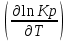 p+RilnPi p+RilnPiG=H–RTlnKP–RT2 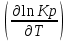 p+RTilnPi сокращаем ,= (1) p+RTilnPi сокращаем ,= (1)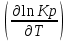 p = p = 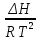 P = const : 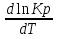 = =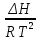 =– =–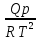 – урав. изобары хим. реакции Вант-Гоффа – урав. изобары хим. реакции Вант-ГоффаАналогично из F=–RTlnKC+RTilnCi и F=U+T 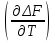 v получаем урав. изохоры хим. реакции Вант-Гоффа : v получаем урав. изохоры хим. реакции Вант-Гоффа :V = const : 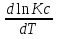 = = 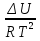 = – = – 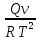 Эти уравнения в дифф. форме показыв. зав-ть К равн. в смеси ид. газов от Т. Если реакция протекает в смеси реал. газов, то КР заменяется на Кf ; КС – на Ка , если реакция протекает в неид. р-ре. Эти уравн. позвол. предвидеть зав-сть Кр от Т : если Н 0, то 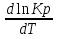 0, т.е. КР растет с ростом Т. 0, т.е. КР растет с ростом Т.17.1 Отклонения от законов идеальных растворов, причины отклонений. З. Рауля не выполн. для реал. р-ров. Парц. давления (или летучести) этих р-ров > или < давлений (или летучестей) паров ид. р-ров. Отклонения от з. Рауля в 1м случае - положительные (общее Р пара > аддитивной величины), а во 2м случае – отрицательные (общее Р пара < аддитивной величины). P2 P2 P1 P1 А Б А Б «+» откл.: Н2О – СН3ОН «-» откл.: Н2О – HNO3 , CCl4 – C6H6 , CCl4 – CH3C6H5 CHCl3 – CH3COCH3 Бывают настолько сильные отклонения от з.Рауля, что появляются точки экстремумов. Причины отклонения - если разнородные молекулы в р-ре взаимно притягиваются с меньшей силой, чем однородные, то это облегчает переход молекул из жидкой фазы в газовую (по сравнению с чистыми жидкостями) и будут наблюдаться «+» отклонения. - Усиление взаимного притяжения разнородных молекул в р-ре (сольватация, образование водородной связи, образование хим. соединения) затрудняет переход молекулы в газовую фазу и поэтому будут наблюдаться «-» отклонения. Процессы взаимного удаления однородных молекул при образовании р-ра сопровождаются поглощением теплоты, поэтому в 1м случае теплота смешения чистых компонентов будет положительной. Во 2м случае, при более сильных взаимодействиях разнородных молекул, теплота смешения компонентов будет отрицательной. Т.о., знак отклонения от закона Рауля и знак теплоты смешения совпадают. 17.2 Диаграммы состояния 2х компонентных систем с хим. соед., плавящимися конгруэнтно и инконгруэнтно. Диаграмма системы, где соединение плавится конгруэнтно (без разложения). Диаграмма представляет собой сочетание 2х диагрм отдельных диаграмм 2х компон. систем: - 1 отвечает системе в-во А хим. соед. AmBn, - 2 отвечает системе хим. соединение в-во В. Каждая диаграмма имеет свою эвтект. точку. К каждой из этих диаграмм приложимо все, что приложимо для диаграммы системы с простой эвтектикой. В точке с : С = 1 2 + 1 = 0 ; компонент 1 хим. соединение. При одной и той же Т кристал. хим. соединение м.б. в равновесии с 2мя разл. расплавами (на-р, с d и е). По хар-ру максимума, отвечающего Т плав. хим. соединения (точка с), можно судить об его прочности. Чем прочнее соединение, тем острее max. Част. разложение соединения при плавл. понижает Тпл и сглаживает max. Расплав а С Расплав + кристаллы А d e расплав + крис. AmBn b крис. AmBn крис. В+ Кристаллы А + AmBn + расплав расплав Кристаллы В + AmBn А Э1 AmBn Э2 В Если 2 в-ва образ. несколько устойчивых хим. соединений, то диаграмма состояния распадается на ряд диаграмм 2х компон. систем. Примеры диаграмм с химическими соединениями: CuCl - FeCl3 (одно соединение); K - Sb (два соединения острый максимум и сглаженный). 18.1 Огр. взаим. р-ть жидкостей. Р-ть газов в жидкостях. З. Генри, Дальтона, Сеченова. Влияние t0. 3 случая смешивания жидкостей: 1)Жидкости в любых соотношениях с образованием однородного раствора (вода – глицерин, вода – этанол). 2)Смешиваются частично (вода – анилин, вода - фенол) 3)Практически не смешиваются (вода – бензол, вода - ртуть). Если смешать примерно равные кол-а воды и анилина, система будет состоять из 2х слоев жидкости; верхний слой – р-р анилина в воде, нижний – р-р воды в анилине. Для каждой t оба раствора имеют строго определенный равновесный состав, не зависящий от кол-а каждого из ком-в. Область под кривой – это область расслаивания жидкостей. Повышение t приводит к увеличению взаимной раст-и), и при некоторой критической температуре расслоения (Ткр ) взаимная растворимость воды и анилина становится неограниченной. В некоторых случаях наблюдаются нижние критические Т раст-я (система вода – триэтиламин). 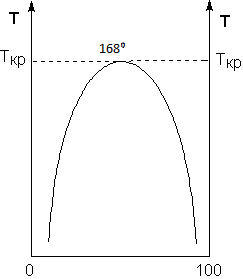 2100 600 Овал это диаграмма для вода-никотин. Полная смешиваемость достигается при повышении и при понижении t0. Растворимость газов в жидкостях. В любой жидкости газ растворим предельно. При некоторой конц. газа образуется равновесие р-р -газ – насыщенный р-р. Раство-ть зависит от T, Р (наружнее), а также от природы 2х, при повышени давления она увеличивается. Закон Генри – раст-ть газа пропорционально давлению над раствором. 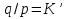 . Если выразить через Менделеева-Клапейрона где g (масса газа) . Если выразить через Менделеева-Клапейрона где g (масса газа) 18.2 Трехкомпонентные системы. Способы изобр. состава. Диаграмма с тройной эвтектикой. Жидкие 3компонентные системы могут состоять из жидких в-в, как дающих р-ры любого состава, так и взаимно ограниченно растворимых. Для построения полной диаграммы состояния 3компон. системы нужна система координат из 5 взаимно ┴ осей. Ее построить невозможно. Часто принимают Т, Р = const; строится 2мерная диаграмма, где отражают различные состояния системы и фаз.переходы. Состав 3компон. системы удобно изображать при помощи ∆ Гиббса. Вершины равносторон. ∆ отвечают содержанию в системе 100% каждого из компонентов А, В и С. Стороны ∆ позволяют описать составы 2компон. систем А + В, В + С, С + А. Точки внутри ∆ описывают составы 3компонентных систем. Метод определения состава основан на том, что сумма перпендикуляров, опущенных из любой точки внутри равносторон ∆ на каждую из сторон, равна высоте ∆. Если принять, что длина всей высоты ∆ отвечает 100 мольным (или весовым) %, то состав тройной системы можно выразить с помощью длин этих ┴ - ов. Из вершины опускаем перпендикуляр, его длина будет отвечать содержанию компонента. Другой способ Розебума. Состав тройной системы, представленой любой точкой внутри ∆ концентраций определяют по трем отрезкам на одной из сторон. Для этого через точку проводят прямые параллельные 2м сторонам ∆. При этом третья сторона разбивается на три отрезка, по длине которых судят о составе. 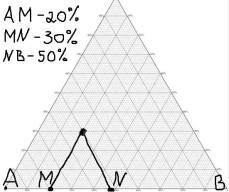 ЗДМ. Связь м/у равновесными концентрациями (или парц. давлениями) в-в, участвующих в хим. реакции, выражается ЗДМ, кол-венная формулировка и вывод были даны Гульдбергом и Вааге (1867). 1А1+2А21А1+2А2 ; v1=k1 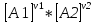 скорость прямой реакции ; скорость прямой реакции ; v2=k2 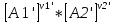 скорость обратной реакции ; v1=v2 в сост. равновесия скорость обратной реакции ; v1=v2 в сост. равновесияk1 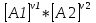 = k2 = k2 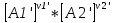 КС = k1 / k2 = 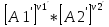 / /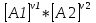 (КСконстанта равновесия, выраженная через концентрации) ЗДМ можно вывести из урав. ii = 0 , если химические потенциалы выразить как функции концентраций, парциальных давлений и т.д. компонентов, участвующих в реакции : [i = Gi (T) + RT ln Ci ], [i = Gi(T) + RT ln Pi ], [i = Gi(T,P) + RT ln Ni] если компоненты идеальные газы [i = i (T) + RT ln fi ] если компоненты идеальные растворы [i = io (T) + RT ln Ni ] если компоненты реальные газы [i = io (T) + RT ln ai ] если компоненты реальные растворы Выведем ЗДМ для газовой реакции, если компоненты идеальные газы. Исходное уравнение i = Gi(T) + RT ln Pi подставим в уравнение ii = 0. i Gi(T)+RTi ln рi, равн=0; ilnрi, равн= 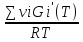 =f(T) =f(T)Опустим индекс (равн); заменим сумму логарифмов логарифмом произведения рi ; а f (T) логарифмом некоторой функции КР (Т) : ln 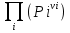 = =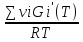 =lnKP(T); =lnKP(T); 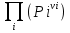 = =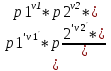 = KP (T) = KP (T)Величина КР, выраженная ч/з равновесные парц. давления в ид. газовой смеси, есть функция только Т и не зав. от суммарного Р и парц. давлений компонентов в исх. смеси. При T = const KP = const. КР константа хим. равновесия , а уравнение - закон действия масс. Если газ реал., то таким же путем получим : Kf = 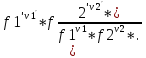 ; Kf KP при Р0 ; Kf KP при Р0В применении к конкр. хим. реакции: N2 + 3H2 2NH3 KP = 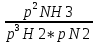 ; Kf = ; Kf = 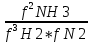 Вид выражения для КР и ее числ. значение зав. от того, в каком направлении и для каких кол-в записано стехиометрическое уравнение реакции : 1/2N2+3/2H2NH3; 2NH3N2+3H2 ; КР= 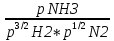 = =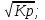 КР= КР=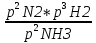 = =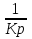 Необх. различать Кр, выраженные разн. способами, т.к. их числ. значения разные. KP= 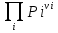 ; KC= ; KC=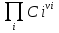 ; KN= ; KN=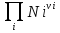 Связь м/у ними можно установить, используя уравнения для ид. газовой смеси : Pi=CiRTKP=KC (RT) ; Pi=NiPKP=KN P ; =1+2+3+...123... Т.к. КР не зависит от Р (для ид. газов), то и КС от него не зависит. KN же зависит от Р и не зав. от исх. кол-в компонентов. Если = 0, т.е. реакция протекает без изменения числа молекул, то КР = КС = КN . dG = VdP – SdT + idni ; i= 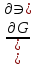 p,T,n p,T,n i– хим. потенциалы – частные производные потенциалов по массе i-го компонента при постоянстве V, T, 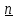 (P, T, (P, T, 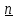 ). ). Хим. потенциал = приросту F (G) при внесении в систему 1 моля данного компонента, если мы рассм. такую систему как бесконечно большое кол-во р-ра определенного состава; при этом V, T (P, T) = const (б/б кол-во р-ра – только в этом случае добавление в р-р 1 моля компонента не изменит состав р-ра, т.е. конц. компонентов). Кроме того : i = 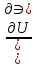 V,S,n = V,S,n = 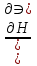 p,S,n= p,S,n= 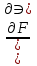 V,T,n = V,T,n = 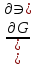 p,T,n p,T,nт.е. химический потенциал компонента раствора данного состава имеет определенное числовое значение; абсолютное его значение определить не умеем. Уравнения Гиббса-Дюгема. dG = VdP – SdT + idni При P, T = const dG=idni Функция G = G(n1, n2, … ) облад. след. св-вом : если массы всех компонентов системы возрастают в одно и то же число раз, то и G возрастает в то же число раз (величина G = U – TS + PV возрастает пропорционально массе, т.к. U, S, V возрастают пропорционально массе). Т.о., интегрируя вышеприведенное уравнение при постоянном составе р-ра, получим : G = ini При указанных условиях величины i остаются пост. в –ц- нарастания m, т.е. (при Р, Т = const) они зав. только от состава р-ра и явл. факторами интенсивности. Можно определить хим. потенциал как изобар. потенциал системы, приходящийся на 1 моль компонента. dG = n1d1 + n2d2 + … + nidi + 1dn1 + 2dn2 + … + idni = nidi + idni При Р, Т = const nidi = 0 (1) Для бинарного раствора : n1d1 + n2d2 = 0 d2 = – 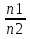 d1 = – d1 = – 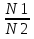 d1 (2) d1 (2)(N1, N2 – мольные доли компонентов). Урав. (1) – (2) – уравнения Гиббса-Дюгема. ни одна из 3 фаз не стремится перейти в др., но при длительной выдержке или при внесении кристаллов моноклин. S все 3 фазы переходят в S моноклинную, кот-я явл. единственной устойчивой фазой при условиях т. О. Точно так же метастабильными явл. двойные равновесия ОА, ОВ, ОС. T Если Sромб быстро нагревать, то она не успевает перейти в Sмонокл ; вместе с тем кристал. решетка Sромб не может выдерживать неограниченного перегрева. При Т кривой ОВ кристаллы распадаются с образованием жидкой фазы, кот-я в данных усл. тоже неустойчива отн-но Sмонокл . ОА и ОС представляют собой соотв-но кривую возгонки перегретой Sромб и кривую кипения переохлажденной жидкой S. Хим. потенциалы Sр и Sм м.б. выражены через хим. потенциалы равновесных с ними паров: Sp=o+RTlnPSp; Sм=o+RTln PSм . o одинаково в обеих формулах, т.к. Т модификаций одинакова. будет > у той модификации, давл. насыщенных паров которой выше. T Кривая давления пара Sр (ЕАО) и кривая давления пара Sм (DАС) пересек. в т. А, лежащей ниже кривой давления пара жидкости КСО.
Такие взаимные превращения 2х кристал. модификаций, кот-е могут протекать самопроизв. и в прямом, и в обратн. направлении в зав-ти от усл, наз-ся энантиотропными. Если исходить из жид. S, переохлажденной до t1 или t2, то в первую очередь обычно выкристаллизовывается менее устойчивая модификация, кот-я уже после достаточной выдержки при той же Т переходит в более устойчивую модификацию. p t2 t1 151oC,1288 атм O Sгаз Sромб Sжидк A 95,5°C E D K B Sмонокл По правилу Оствальда, в случае возможности ряда фазовых переходов от менее устойчивого состояния ко все более устойчивым обычно образуется ближайшая более устойчивая модификация, а не самая устойчивая. Иногда кривые давления паров 2х кристал. модификаций (н-р, бензофенона) должны пересечься выше кривой давления пара над жидкой фазой. Обе модификации плавятся в точках Х и Y; Р пара модификации I во всей области существования кристаллов выше Р пара модификации II, а следовательно, самопроизвольные превращения возможны лишь в направлении I II, н-р, после того, как из жидкой фазы, переохлажденной до Т1, выделится модификация I. Точка пересечения О не может быть получена экспериментально. Она находится графически путем продолжения опытных кривых АХ и ВY. p |
