Шпоры по физхимии. 1 Энергия, теплота, работа. Первый зн термодинамики. Внутренняя энергия и энтальпия фи состояния системы
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
U –TS + PV =G – энергия Гиббса, ф-ия состояния системы.G = U – TS + PV = F + PV = H – TS ; G = H – TSИзобарный потенциал – функция Р и Т :G = F + PV,dG =dF + PdV+VdP;dF=– PdV– SdT;dG = – PdV – SdT + PdV + VdP dG = VdP – SdT , G = G(P,T) dG = 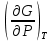 dP + dP +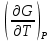 dT ; dT ;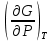 = V , = V ,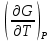 = – S;V –мера прироста G с ростом Р при T = const = – S;V –мера прироста G с ростом Р при T = constS – мера убыли G с ростом Т при P = const.С учетом неравновесных процессов:dG VdP – SdT.Если P,T = const (G)P,T 0 Изобарный потенциал системы при P,T = const уменьшается при неравновесных процессах и постоянен при равновесных процессах; равновесное состояние системы соответствует минимуму G. (G)P,T0– критерий самопроизвольного протекания процесса в сист., находящейся при P,T=const; (G)P,T = 0 , ( 2G)P,T 0– критерий равновесия в системе. Если есть другие виды работы, кроме работы расширения, то: (G)P,T – A ,т.е. условие равновесия должно быть усложнено: введено дополнительное условие постоянства некоторых других параметров, кроме Р и Т. ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ. F и G принадлежат к классу ф-ий состояния системы, наз. термодинамическими потенциалами: 1.размерность (Дж/кмоль); 2. Служат критериями самоп-ного протекания процессов (процессы протекают в сторону их уменьшения); 3. Их мин. значения отвечают (при тех же условиях) равновесию системы и являются условиями равновесия. U и H – тоже термодинамические потенциалы. Q = dU + A TdS; dU TdS–PdV 10. 2.Полиморфизм: монотропия и энантиотропия. Диаграмма состояния серы. p t2 t1 151oC,1288 атм O Sгаз Sромб Sжидк A 95,5°C E D K B Sмонокл Кристаллическая сера в2х модификациях ромбической и моноклинической. S образует 4 фазы: 2 кристаллические, жидкую и пар; Линии на диаграмме отвечают условиям, при которых возможно равновесное сосуществование двух фаз; 3 тройные точки : А, В, С. Кроме того, существует еще 1 тройная точка О, в которой могут сосуществовать перегретая ромбическая S, переохлажденная жидкая S и пересыщенный пар. 3 т/д неравновесные фазы могут образовать метастабильную систему(относительной устойчивости) Метастабильность заключается в том, что ни одна из 3х фаз не стремится перейти в другую,но при длительной выдержке или при внесении кристаллов моноклинической S все 3 фазы переходят в S моноклинную, которая является единственной т/д устойчивой фазой при условиях точки О.Метастабильными явл-ся двойные равновесия ОА, ОВ, ОС. Если Sромб нагревать быстро, то она не успевает перейти в Sмонокл ; вместе с тем кристалл. решетка Sромб не может выдерживать неограниченного перегрева. При Т кривой ОВ кристаллы распадаются с образованием жидкой фазы, которая в данных условиях тоже неустойчива относительно Sмонокл . Кривые ОА и ОС представляют собой соответственно кривую возгонки перегретой Sромб и кривую кипения переохлажденной жидкой S. Хим. потенциалы Sр и Sм м. б. выражены ч/з хим.пот-лы равновесных с ними паров:Sp=o + RT ln PSp Sм = o + RTln PSм o одинаково в обеих формулах, т.к. Т сопоставляемых модификаций одинакова. будет больше у той модификации, Р насыщенных паров которой выше. Кривая давления пара Sр (ЕАО) и кривая давления пара Sм (DАС) пересекаются в т. А, лежащей ниже кривой давления пара жидкости КСО. при t 95,5оС P пара Sм P пара Sр и при этих t (н-р, при t1) возможен самопроизвольный переход Sм Sр . при t 95,5о (н-р, t2) P пара выше у Sр и должно идти превращение Sр Sм. Такого типа взаимные превращения двух кристалл. модификаций, которые могут протекать самопроизвольно и в прямом, и в обратном направлении в зав-ти от условий, называются энантиотропными превращениями. Если исходить из жидкой S, переохлажденной до t1 или t2, то в первую очередь выкристаллизовывается менее устойчивая модификация, которая уже после достаточной выдержки при той же Т переход. в более уст. модификацию. Согласно правилу Оствальда, в случае возможности ряда фазовых переходов от менее устойчивого состояния ко все более уст. обычно обр-ся ближайшая более уст. модификация, а не самая уст.. Бывают случаи, когда кривые P паров 2x кристалл.модификаций (н-р, бензофенона) должны пересечься выше кривой давления пара над жидкой фазой. 11.1.Уравнения max работы Гиббса-Гельмгольца, их вывод и анализ. Св-ва функций F и G дают возм-ть установить связь м/у max работой равновесн. процесса и теплотой того же процесса, но протек. неравновесно. 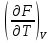 = – S, F = U – TS, F = U + T = – S, F = U – TS, F = U + T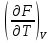 Запишем это урав. для 2х состояний системы: F1 = U1 + T 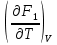 , F2 = U2 + T , F2 = U2 + T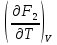 , ,F1 – F2 = U1 – U2 + T 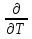 (F1 – F2)V = – F (F1 – F2)V = – FAmax = 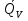 + T + T 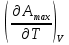 (1) (1)Зная Amax (или F) и зависимость ее от Т, можно вычисл. теплоту процесса (т.е. U). Если же известна Q процесса, то для расчета Amax необх. интегрировать (1), причем появл. const интегрирования, для опред. которой необходимы доп. сведения. Урав. (1) – урав. Amax (уравнение Гиббса-Гельмгольца) – может быть записано и в форме: F = U + T 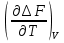 (2) (2) Др. варианты записи уравн. Гиббса-Гельмгольца: 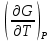 = – S , G = H – TS , G = H + T = – S , G = H – TS , G = H + T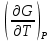 ; ;G1 = H1 + T 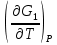 , G2 = H2 + T , G2 = H2 + T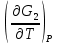 ; ;G1 – G2 = H1 – H2 + T 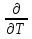 (G1 – G2)P ; (G1 – G2)P ;Amax = 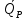 + T + T 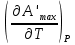 (3) (3) G = H + T 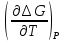 (4) (4)11.2 Активности компонентов раствора. 3 шкалы активности. Урав. для хим. потенц. компонентов реал. р-ра :(1) i = iо (T) + RT ln (Pi / Pio) пар – ид. газ; (2)i = iо (T) + RT ln (fi /fio) пар – реал. газ. Урав. для хим. потенц. компонента в ид. р-ре : (3)i=iо(T)+RTlnNi. Отношение Pi/Pio(или fi /fio) играет такую же роль в ур. для реал. р-ра, что и мол. доля Ni в урав. для ид. р-ра. Это отношение наз-ся термодинам. активностью компонента р-ра (или активностью компонента) : ai=Pi/Pio; ai = fi /fio (4)i=iо (T) + RT lnai – выраж. для хим. потенц. любого неид. раствора. Используя его, можно для любого реал. р-ра получить термодинам. уравнения, которые будут иметь тот же вид, что и урав. для ид. р-ра, но вместо Ni – ai. При наличии разных значений компонента в разл. частях изотерм. системы компонент переходит из части системы с большим знач. в часть с меньшим значением. В ид. р-рах компонент самопроизв. переходит от части р-ра с большей конц. этого компонента в часть с меньшей конц.; в реал. р-рах компонент переходит в направлении меньших величин ai. При равновесии эти величины равны во всех частях р-ра в одном р-ле, м/у которыми возможно своб. перемещение компонента. Термодинам. хар-кой компонента р-ра м.б. его Pi или fi в насыщ. паре над р-ром. Однако эти величины для мало летучих компонентов практически неопределимы, тогда как ai м.б. определена не только из уравнений,но и др. методами. Метод активности – формальный прием, он закл. во введении новой функции состояния, промежуточной м/у хим. потенц. и конц.. Он ничего не дает для понимания причин отклонения от закона ид. р-ров. Но он упрощает матем. разработку термодинамики р-ров. аi– отн. летучесть ( или отн. давление пара), т.е. отношение летучести при дан. условиях к летучести в известном станд. состоянии. Для станд. состояния летучесть равна fio и ai = 1. Станд. состояние – чистый жидкий компонент при той же Т. Но часто приходится выбирать иные станд. состояния, т.к. большое число в-в в широком интервале Т сущ. в тв. состоянии и давления насыщ. пара компонента часто ничтожно малы в опытных условиях. Изотермы ai – Ni для бинарных смесей : 12.1.Статистический хар-р 2 закона термодинамики. Ур. Больцмана, его вывод и анализ. Термодинам. метод неприменим к системам, сост. из малого числа молекул. Это связ. с тем, что в таких системах исчезает различие м/у Q и А. Также исчезает однозначность направления процесса, устанавливаемая 2 зак. термод.. Утверждение о невозможности одного из направлений процесса заменяется оценкой отн. вероятности обоих направлений. Для очень малого числа молекул оба направления процесса стан. равноценными. Механическое движение отд. молекул обратимо и преимущ-го направления не имеет. В отличие от I закона термодинамики, который является абсолютным, II з. термод. имеет статист. хар-р, он справедлив лишь для систем с большим кол-вом частиц. Ограничения перевода Q в А, который устан-ся 2 з., в противоположность неогранич. переводу А в Q, связаны со стремлением системы, сод. большое число частиц, к молекул. беспорядку, мерой которой явл S. А характер-ся упорядоч. коллективным движ. частиц в одном направлении; Q связана с хаотич. молекул. движением. Поэтому выясняется самопроизв. хар-р перехода А в Q как перехода молекул. системы к более вероятному состоянию (с большей степенью молек. беспорядка). Причина стремления к равновесию - переход молекуляр. системы от менее вероят. состояния к более вероятному, при этом S ↑. Связь м/у S и вероятностью состояния системы можно устан. т.о.: любое термодинам. макросостояние системы может быть осуществлено различ. микросостояниями. Термодинам. вероятность W - число микросостояний, с помощью которого можно осущ. данное макросостояние системы W = 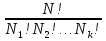 N – общ. число молекул, распредел. либо по kотделениям, либо поk уровням, либо по скоростям и т.д.; N1 – число молекул в 1-м отделении и т.д. Рассм., как меняется W по мере протекания процесса. Самопроизв. процесс сопровожд. ↑ S; при этом резко ↑ W. След., S и W д.б. связаны друг с другом:S = S (W). Надо учесть аддитивность S: S=S1+S2; Для W: W=W1 W2 (вероятность события = произведению вероятностей отд. независ. событий). 12 2. Осмос. Вывод уравнения осмотического давления. Равновесие осущ-ся при равенстве Т и p во всех частях всех фаз, составляющих систему, и при постоянстве состава во всех участках одной фазы. При наличии разностей хим. потенциалов компонентов м/у участками одной фазы или между разными фазами эти компоненты диффундируют в направлении падения своего хим. потенциала до тех пор, пока не будет достигнут одинаковый состав во всех участках внутри каждой фазы и равновесное распределение компонентов м/у фазами. Необходимым условием достижения такого равновесия является возможность свободного перехода всех компонентов из одного участка каждой фазы в другой участок и из одной фазы в другую. Иная ситуация наблюдается, когда отдельные части системы разделены перегородками, кот. непроницаемы для одних компонентов (пр.: растворенное в-во) и проницаемы для других (пр.: растворитель). Расм. рисунок. Сосуд 1 содержит водный раствор какого-либо вещества; закрыт внизу полупроницаемой перегородкой. Сосуд 1 помещен в сосуд 2 с водой. Вода будет проходить из сосуда 2 в сосуд 1. Такой самопроизвольный переход воды (или р-ля) через полупроницаемую перегородку в раствор наз. осмосом. Сила (на единицу площади), заставляющая р-тель переходить через полупроницаемую перегородку в раствор (находящийся при том же внешнем р, что и р-ль), наз. осмотическим давлением. Уровень р-ра в сосуде 1 повышается, создавая допол-ное давление, которое препятствует осмосу. При высоте h столба жидкости в сосуде 1 допол-ное Р достигает такой величины, при j осмос прекращается, т. е. устанавливается равновесие м/у р-ом данной концентрации и чистым р-ем, разделёнными полупроницаемой перегородкой. Впервые осмотическое давление () измерил Пфефер (1877) Для р-ов с с 0,3 моль/л V = 22,6 латм/моль (для идеальных газов рV = 22,4; V – объем, заключающий 1 2 1 моль растворенного вещества); при более высоких к-циях V растет. Зависимость от Т: Т. Рассмотренные закономерности осмотического P разбавленных р-ов охватываются уравнением Вант-Гоффа : = cRT, (с – молярная концентрация;  ) )Т.о., разбавленных растворов численно равно тому P, J производило бы то же число молекул растворенного вещества, если бы оно в виде ид. газа занимало при данной Т объем, равный объему р-ра. 13.1.Термодин. потенциалы идеальных и реал. газов. Летучесть реал. газа и ее расчет. 1. U 1 моля ид. газа, зависящая только от Т: dU=CV dT , U=Uo+ 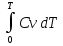 2. H: H=U+PV=Uo+ 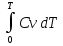 +RT=Uo+ +RT=Uo+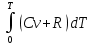 =Uo+ =Uo+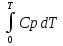 3.S: S=CVlnT+RlnV+So , S=CPlnTRlnP+So 4. dF= –PdV–SdT , dG=VdP–SdT Пусть T=const: dF= –PdV= – 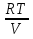 dV, dG=VdP= dV, dG=VdP=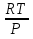 dP; F= –RTlnV+F(T) , G=RTlnP+G(T) dP; F= –RTlnV+F(T) , G=RTlnP+G(T) Для реал. газов Льюис предложил формальный прием, кот-й позвол. связать найденные опыт. путем св-ва реал. газа с его термодин. пар-рами и изучать т.о. термодинам.закономерности в реал. газ. системах. Вводится новая функция f – термодинам. летучесть (летучесть, фугитивность. f подставл. в урав. вместо Р. G=RTlnf+G(T) (1). При этом вводится условие: lim f/P= 1 при Р 0 (2). f - функция, промежуточная м/у пар-рами состояния газа Р и Т, с одной стороны, и G – с другой стороны. G = G2 – G1 = RT lnf2 / f1 при T=const. Чтобы вычисл. G для процсов с реал. газом, нужно знать зав-ть f от Р и Т. Продифференцируем ур.(1) по Р при Т =const  ( 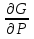 )T=RT( )T=RT(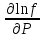 )T; Т.к. ( )T; Т.к. (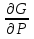 )T=V, то V=RT( )T=V, то V=RT(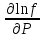 )T; )T; 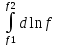 = =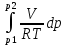 , ln , ln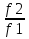 = =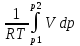 Надо знать зав-ть V от Р. Наиб. точный способ закл. в граф. нахождении интеграла. По эксперим. значениям V строят кривую зависимости V от Р. Интеграл = площади под кривой. Зная V=V(P), вычисл. объемную поправку реального газа : V= 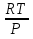 –, 0 при не слишком высоких Р –, 0 при не слишком высоких Рln 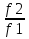 = = 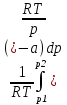 =ln =ln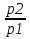 – – 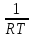 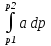 , надо знать , надо знать =(Р); ln f2–ln f1=lnP2–lnP1– 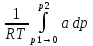 Пусть нижний предел интегрирования Р1 очень мал, так чтобы f1 = P1 : ln f =lnP – 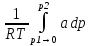 ; ln ; ln 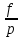 = – = –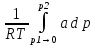 , , 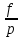 =exp (– =exp (– 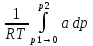 ) ) = 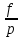 - коэф. активности или коэф. летучести газа. - коэф. активности или коэф. летучести газа.Изобразим зав-ть = 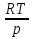 – V от Р, характерную для многих реал. газов при обычной Т: – V от Р, характерную для многих реал. газов при обычной Т: |
