Шпоры по физхимии. 1 Энергия, теплота, работа. Первый зн термодинамики. Внутренняя энергия и энтальпия фи состояния системы
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
|
O Y X I A B II T T1 Взаимные превращения кристаллических фаз, которые могут протекать самопроизвольно лишь в одном направлении, называются монотропными. Факторы, вызывающие полож. и отриц. отклонения, могут действовать в р-ре одновременно (особенно наглядно видно при изменении знака с изменением концентрации). Отсутствие отклонения от закона Рауля или равенство нулю теплоты смешения при образовании р-ра одного какого-либо состава не являются признаками того, что данные компоненты образуют идеальные растворы. Если интервал Т небольшой, то H = const. d ln KP = 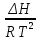 dT ; ln (Kp2/Kp1) = dT ; ln (Kp2/Kp1) = 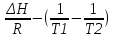 = = 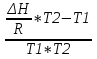 lg(Kp2/Kp1) = 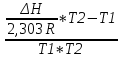 Если знаем Н и КР1 (КР2), то можно рассч. КР2 (КР1) Если знаем Н и КР1 (КР2), то можно рассч. КР2 (КР1) ln KP=– 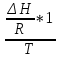 +const(1) ; tg=– +const(1) ; tg=–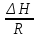 ; HT=Ho+ ; HT=Ho+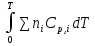 (Ho – пост. интегрирования уравненияя Кирхгоффа и не имеет физ. значения теплоты реакции при Т = 0) или HT2=HТ1+ 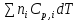 СР=a+bT+ 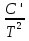 или СР=a+bT+cT2+dT3; HT=Ho+aT+bT2+cT3+… или СР=a+bT+cT2+dT3; HT=Ho+aT+bT2+cT3+…dlnKP = 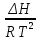 dT = dT = 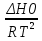 dT+ dT+ 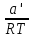 dT+ dT+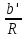 dT+ dT+ 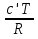 dT+… dT+…lnKP= – 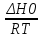 + +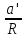 lnT+ lnT+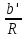 T+ T+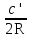 T2+…+const T2+…+constЧтобы найти const, нужно знать экспериментально определить КР для одной Т. Gо = RTlnKP (Gостанд. изобар. потенц. реакции – если Рi=1 – парц. Р всех участников реакции в исх. смеси) G = H – TS , GTo=HTo–TSTo (о означает, что величины станд.; Т – любая) RTlnKP=HTo–TSTo при Т=const; lnKP= – 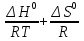 (2) (2)Сравнение ур. (1) и (2) для lnKP показывает, что Н=Но в урав. изобары хим. реакции; tg= –Ho/R ; const=So/R . 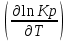 p= p= 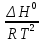 – уравнение изобары – уравнение изобарыПри N=1, f2=k=f o2 ; f2=f o2 N. В неид. р-рах kf o2 Для многокомп. ид. р-ра: fi= f oi Ni (4) При невысоких Т, когда парциальные давления компонентов невелики и летучести компонентов близки к их парциальным давлениям, возвращаемся к закону Рауля в форме уравнения (1), а уравнение (3) приобретает вид:Р2 = kN – з. Генри: парц. Р пара раствор. в-ва пропорционально его N. k – коэф. Генри. В ид. р-ре при малых Р нас. пара, когда f2 = P2, k=Po2 и P2=P o2 N (6) В общем виде для многокомпонентного ид. р-ра при невысоких Р: Pi = P oi Ni (7)
Полное Р пара ид. бинарного р-ра: Р = Р1 + Р2 = Ро1 – (Ро1 – Ро2 )N ; Р – линейная функция N. Примеры ид. р-ров : дибромпропан–дибромэтан, бензол–толуол, гексан–октан. В общ. случае составы ид. р-ра и его насыщ. пара не совпадают: N = 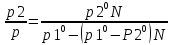 N – конц. 2-го компонента в паре; N = N при всех конц. только в том случае, если Ро1 = Ро2. Для хим. потенциала компонента р-ра: 2=о2(T) + RTln (P2/P20) ; 2=о2(T) + RTln ( f2 / f20 ) Учитывая (из ур. (7) и (4)), что Pi / Poi = Ni , fi/ f oi = Ni , получаем урав. для хим. потенциала компонента ид. жидк. р-ра, совпадающее по форме с урав. для i ид. газ. смеси: i = оi(T) + RTln Ni Часто Р пара р-ля при малых конц. остальных компонентов следуют з. Рауля и в р-рах, не явл. ид., т.е. в сильно разбавл. р-рах. Для них Р1=Po1 (1 – N) и одновременно P2 = kN , где k Р o2. Такие р-ры - предельно разбавленные. При образовании ид. р-ров из чистых жидких компонентов Q не погл. и не выдел., а V р-ра = сумме объемов жидких компонентов. Если смешать два компонента А и Б, то образуется два жидких слоя. Состав этих слоев изображен точками п и р на ∆ Розебума. Добавляемый компонент С распределяется между двумя слоями, при этом можно получить ряд тройных сопряженных растворов. Соединяя линией точки составов сопряженных растворов получим бинодальную кривую (akb). Любая смесь А,Б и С распадается на два сопряженных тройных раствора (их состав – точки а и b). Смесь трех компонентов это фигуративная точка x внутри гетерогенной области. При добавлении компонента С два сопряженных тройных раствора становятся все менее различимы, в результате достигается точка k – критическая. В ней составы одинаковы. В итоге состав сопряженных фаз (это точка x) можно определить приближенно по правилу Тарасенкова: продолжения всех каннод пересекаются в точке D. Проведя из т. D касательную к кривой расслаивания, найдем т. k, отвечающую составу x. Точка k обычно расположена ассиметрично. k a b х А п р В D растворена в V1 (объем ж-ти): 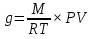 , , 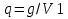 => =>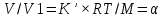 . – коэффициент растворимости газа – не зависит от Р (для ид. и предельно разбавл р-ов ид. газов). показывает, сколько объемов газа растворяется в 1 объеме раствора при данной Т. Растворимость газа может быть также выражена в объемах газа, приведенных к 0 0С: . – коэффициент растворимости газа – не зависит от Р (для ид. и предельно разбавл р-ов ид. газов). показывает, сколько объемов газа растворяется в 1 объеме раствора при данной Т. Растворимость газа может быть также выражена в объемах газа, приведенных к 0 0С: 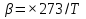 – коэффициент поглощения газа. При постоянной t0 раст-ть в данной жидкости каждого из компонентов газовой смеси, находящейся над жидкостью, пропорциональна их парциальному давлению. 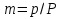 p (малое) парциальное. В этом закон Дальтона. Присутствие в растворе 3го компонента влияет на р-ть газов. В солевых растворах растворимость газов, как правило, меньше, чем в чистой воде. Это высаливание. Зависимость растворимости газа в водном растворе соли от концентрации соли (с) выражается формулой Сеченова : 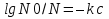 , где N и No – мольная доля газа в солевом р-ре с конц. с и мольная доля в р-ре в чистой воде, соответственно. k – const, характерная для данной соли. , где N и No – мольная доля газа в солевом р-ре с конц. с и мольная доля в р-ре в чистой воде, соответственно. k – const, характерная для данной соли.Высаливающее влияние объясняется, в основном, тем, что ионы притягивают молекулы воды (гидратация ионов) и не притягивают неполярные и малополярные молекулы газов. Происходит связывание части воды, которая не будет являться растворителем, поглощающим газ. Растворение газов в жидкостях сопровождается выделением теплоты. Поэтому растворимость газов при данном Р уменьшается с ↑ Т (по принципу Ле-Шателье) Газ + раст-ль < = > раствор + Qp . Равновесии смещается ВЛЕВО. Диаграмма состояния системы, в которой соединение, плавится инконгруентно (с разложением). Притаком плавлении составы исходной тв. фазы и получаемой жидкой не совпадают. Н-р: система СaSiO3 + BaSiO3. Соединение полностью разлагается ниже своей Т пл. Расплав А + В 3 2 1 g а Расплав + крис. А d Расплав + i f r c крис. В Расплав + крис Кристаллы А АmBn l + крис. АmBn Кристаллы B + крис. АmBn А АnBm Y B abl(кристаллы В), cdg(кристаллы А),bcfk(кристаллы химического соединения AmBn). 3 возможных случая фазовых превращений для линии cfd. 1 – в исходном составе много А, 2- много Б, 3- много AmBn. При охлаждении каждого из 3х вначале плавится крис. А, затем плавится соед-е состоящее из А и Y. Точка с, отвечающая температуре и составу р-ра, который может находиться в равновесии с двумя кристал. фазами, называется перитектической. Она отличается от эвтектической тем, что оба вида кристаллов, равновесных с расплавом, обогащены одним и тем же компонентом по сравнению с этим расплавом. Также для этой точки еще характерно то, что она является нижней точкой кривой начала кристаллизации одной фазы (А) и верхней точкой кривой начала кристаллизации второй фазы (хим. соединение), тогда как эвтектическая точка является нижней точкой обеих кривых. Особенность инконгруентного плавления - в равновесии с крис. соед-ем (т.f) находится жидкость другого состава (т.c). 19.1 Растворимость тв. в-в в жидкостях. Уравнен. р-ти в ид. и пред. разб. р-рах. Откл. от ид. р-ти Тв. в-во не может беспредельно растворяться в жидкостях: при достижении некоторой конц., определенной при данных Р и Т, тв. в-во перестает растворяться; устанавливается равновесие м/у р-ом и тв. в-вом.Насыщенный р-р – р-р, находящийся в равновесии с тв. в-вом, а его конц. – растворимость тв. в-ва. Хим. потенциалы растворен. в-ва в насыщ. р-ре (нас) и в твердой фазе (т) имеют одно и то же значение. нас = т ; 2, нас = 2о + RT lna2, нас; – RT lna2, нас = 2о – т = G; G = H + T (G/T) (p=const) . ур-е Гиббса-Гельмгольца. Растворимость любова в-ва можно представит ькак несколько фаз: 1)Плавление тв. в-ва 2)Смешение 2х жидкостей. В случае ид. р-ов теплота 2-го процесса = 0. В случае ид. р-ров теплота 2-го процесса = 0. Теплота 1-го процесса – теплотаплавления тв. в-ва Н2, пл . –RT lna2,нас= Н2,пл+ Т –R lna2,нас–RT (ln a2 / T)P,нас ] (ln a2 / T)P,нас = Н2,пл / RT2 Для ид. р-ров : а2 = N2 = N (d ln N / dT)P,нас = Н2,пл / RT2 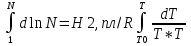 ; To – Т плавления 2-го компонента (N = 1); Т То . ; To – Т плавления 2-го компонента (N = 1); Т То . ln N = –Н2,пл / R (1/T – 1/T0) = –A / T + B. (линейная зависимость lnN от 1/Т). В это уравнение не входят величины, характеризующие растворитель идеальная растворимость вещества не зависит от природы растворителя. 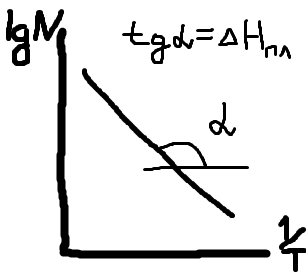 tg a = Н2,пл 19.2 Диаграмма состояния 2х компонентной системы с неогр. взаимной р-тью компонентов. Тв. р-ры (смешанные кристаллы) однородные системы переменного состава (как и жидкие р-ры), т.е. тв. фаза не представляет собой кристаллов чистого компонента. Состоит из 2х или более компонентов, одновременно участвующих в образовании кристаллов и равномерно распределяющихся в нем. Твердые растворы бывают двух типов : 1. Тв. р-ры внедрения атомы (молекулы) растворяемого компонента размещаются в пустых местах решетки растворителя между ее узлами. При условии, что размеры частиц 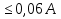 . По мере накопления внедряемого в-ва устойчивость решетки растворителя уменьшается, т.о., имеет место ограниченная р-ть. Пример р-р С в Fe. . По мере накопления внедряемого в-ва устойчивость решетки растворителя уменьшается, т.о., имеет место ограниченная р-ть. Пример р-р С в Fe.2. Тв. р-ры замещения атомы (ионы) растворяемого в-ва располагаются в узлах кристал. решетки вместо атомов растворителя. Важно, чтобы кристал. структуры замещающего и замещаемого компонента были достаточно близки и чтобы радиусы атомов(ионов) совмещались. При этих усл. устойчивыми могут оказаться тв. р-ры любого состава и имеет место неограниченная р-ть компонентов бинарной смеси; можно получить непрерывный ряд тв. р-ров от 0 до 100% каждого компонента. Пример: системы AgCl - NaCl, Au-Ag, Au-Pd, Cu-Ni. Тв. р-ры, компоненты которых взаимно неогран. растворимы Их диаграмма состояния аналогична диаграмме жидкость-пар для полностью смешивающихся жидкостей (их частицы близки по объемам и характеру связи). acf линия ликвидуса ; bdg линия солидуса. Когда фигуративная точка системы лежит на линиях ликвидуса или солидуса, система состоит из одной фазы. Между линией ликвидуса и линией солидуса лежит область значений состава и температур, при которых каждой фигуративной точке всей системы (например, точке е), отвечают две точки (с и d), описывающие составы двух равновесных фаз, на которые распадается система.
Т 1 Когда фигуративная точка Расплав а b системы лежит на линиях t 1 ликвидуса или солидуса, сис- Расплав + тема состоит из одной фазы. t 2 C e d Между линией ликвидуса и Твердый ра-р линией солидуса лежит об- f ласть значений состава и тем- t 3 g ператур, при которых каждой Твердый раствор фигуративной точке всей сис- 2 темы (например, точке е), отвечают две точки (с и d), описывающие составы двух равновесных фаз, на которые распадается система. Соотношение между количествами этих фаз находится по правилу рычага. При охлаждении системы, отвечающей фигур. т.1, состав расплава не меняется до t1. Дальнейшее понижение Т обусловливает выделение тв. р-ра, более богатого В, чем исх. расплав; жидкая фаза при этом обогащается в-вом А (более легкоплавким); Т ее отвердевания понижается. Состав расплава в процессе кристаллизации изменяется по кривой acf , а состав кристаллической фазы по кривой bdg. По мере понижения Т (начиная с t1) охлаждение замедляется, %-ное содержание кристал. фазы растет. Так при t2 в системе ( се / сd * 100%) тв. р-ра. При t3 исчезают следы расплава (состава f) с образ-ем кристалла состава g ; система становится однофазной. После этого происходит охлаждение тв. р-ра. Т.о., при выделении тв. р-ов из жидкой фазы составы жидкости и кристаллов не совпадают (также, как не совпадают составы жидкого раствора и равновесного с ним пара); кристаллизация (и обратный процесс плавление) происходят в некотором интервале Т. Система устойчива в течении всей кристаллизации, если медленно охлаждать. При этом образовавшиеся кристаллы успевают сохранять равновесии с раплавом. При высокой Т это возможно. При низкой Т, диффузия в тв. фазе замедленна и не возможно достичь выравнивания состава крис. фазы. Подобная термодинам.система не устойчива. В тв. р-рах также возможны переходы от огран. р-ти к неогран. при соответствующх крит.Т. Отклонения от ид. р-ти. Р-ть в реал. р-рах сильно отлич. от идеальной. В-ва сходной хим. природы часто имеют совершенно различные р-ти в том или ином р-ле. Точно предсказывать величины р-ти какого-либо в-ва на основании данных для др. в-в пока невозможно. Общие закономерности ограничиваются качествен. обобщениями, охватывающими лишь отд. классы р-ров. Например, неполярные в-ва лучше взаимно растворимы (так же, как и полярные), чем неполярное в-во в полярном растворителе и наоборот. Лишь для неполярных веществ (в основном органических), р-ры которых обнаруживают небольш. полож. отклонения от з. Рауля, удается построить полуколичественную статистическую теорию растворимости. Сложное взаимодействие факторов, определяющих р-ть, приводит к тому, что в некот. случаях р-ть уменьшается с ↑ Т, тогда как кол-венные теории предсказывают ↑ раств-ти с Т. Зависимость раст-ти тв. в-в от Р. Представление о малом влиянии Р на р-ть тв. тел в жидкостях справедливо лишь при небольших Р. В наст. время доступный для исследования диапазон Р расширился до десятков тысяч атмосфер и влияние Р на р-ть оказалось значительным.: (d ln N / dP )T,нас = –V2 / RT – ур-е Планка – Ван-Лаара V2 = V2 – V02,T – прирост объема при растворении 1 моля тв. в-ва в его насыщ. р-ре. Уравнение применимо к ид. и предельно разбавл. р-рам. |
