Шпоры по физхимии. 1 Энергия, теплота, работа. Первый зн термодинамики. Внутренняя энергия и энтальпия фи состояния системы
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
|
1)Мольные доли (N): aN = N; – рациональный коэф. активности ; aN N при N 0 ; aN = N ( указ. на пред. разбавл. р-р) 2)Мольно-объемная концентрация (молярность с) : aC = fc; f – мольный коэф. акт-ти; aC cпри с 0 ; аС = с 3)Моляльность (m): am = m; – практический (моляльный) коэф. акт-ти; am m при m 0; am = m. широко использ. в применении к электролитам; f используется реже. В конц. р-рах все коэф. акт-ти разл. по величине. В разб. р-рах коэф. , f, равны. Давление нас. пара жидкости можно измерить в шир. интервале Т; значит. труднее измерить Нисп. Интервал Т д.б. небольшим, т.к. Нисп изменяется с ростом Т. Более точно Нисп вычисляют по значению dP/dT, кот-е находят, определив наклон касательной к кривой Р = f (Т) при заданной Т.  Зав-ть Нисп от Т: убывает с ростом Т, не сильно изменяясь при средних Т и очень сильно – вблизи Ткр, при которой Нисп становится =0. Зав-ть Нисп от Т: убывает с ростом Т, не сильно изменяясь при средних Т и очень сильно – вблизи Ткр, при которой Нисп становится =0. Нисп различных жидкостей связаны с их НТК: 1. Правило Трутона: Sисп = 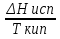 20 – 22 кал/(к*моль) – 20 – 22 кал/(к*моль) – мольные энтропии испарения разл. жидкостей в НТК одинаковы. 2. Урав. Кистяковского (более точное): Sисп = 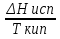 = 8,75 + 4,57 ln Ткип (кал/(к*моль) ) = 8,75 + 4,57 ln Ткип (кал/(к*моль) ) 3. Прав. Гильдебранда – Sисп жидкостей равны м/у собой при Т, для кот-х мольные объемы нас. пара одинаковы, при этом Sисп = 20 – 22 кал/(к*моль) при Vг = 49,5 л/моль. Эти правила не выполн. для ассоциированных жидк. (вода,спирты), и приблиз. выпол. для углеводородов и их произв.,эфиров и др. неполярных в-в. Для Фаз. переходов II рода. хар-но не только рав-во изобар. пот-лов, но и рав-во S и V сосуществующих в равновесии фаз, т.е. отсут. тепл. эффекта процеса и изменения V при Т превращения: G = S = V = 0; Но меняются скачкообразно др. параметры, н-р, СР. Примеры ФП II рода: 1. Скачкообр. изменение СР при превращении 2х модификаций жидкого He при 2,2 К. В некот. интервале Т в-во поглощает значительно большее кол-во Q, чем то, которое соответствовало бы кривой при отсутствии пика. Эта доп. теплота связана с превращением 2-го рода, но она поглощается в некотором интервале Т и вызывает аномальное увеличение СР в этом интервале; при Т максимума кривой теплота не поглощается. 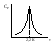 2. Превращения ферромагнитных тел при Т, назыв. точкой Кюри, выше кот-й тела теряют ферромагнитные. св-ва. 2. Превращения ферромагнитных тел при Т, назыв. точкой Кюри, выше кот-й тела теряют ферромагнитные. св-ва. 3.Превращения обычных металлов в сверхпроводники при низких Т. 4.процес распада и образования интерметаллидов в тв. метал. р-рах. Каждая строка позволяет составить (Ф 1) независ. уравнений; общее число независ. уравнений (для i) = К(Ф 1). Независ. переменные - Т, Р и конц. компонентов. В каждой фазе есть К компонентов, но, задав произвольн. значения Р и Т, мы уже не можем выбирать произвольно концентрации всех компонентов; конц. одного из компонентов должна принимать определ. значение. Т.о., число незав. концентраций в каждой фазе = (К 1), а общее число независ. концентраций во всех фазах = Ф(К 1); Р и Т еще 2 независ. переменные. Общее число независ. переменных Ф(К 1) + 2. Если число независ. переменных = числу связывающих их уравнений : Ф(К 1) + 2 = К(Ф 1) , то каждая независ. переменная принимает определ. значение и вся система может существовать только при этом сочетании значений Р, Т и конц. компонентов. Если число урав. < числа независ. переменных, то разность С = Ф(К 1) + 2 К(Ф 1) представ. собой число переменных, которым можно придавать произв. значения при имеющемся числе уравнений и при данном числе фаз. «С» - число термодинам. степ. свободы системы. Системы с С = 1 - моновариантные (одно-), С = 2 бивариантные (двух-), С = 0 нонвариантные. Урав. Гиббса: С = К Ф + 2 (число ст. свободы равновесной термод. системы, на которую из внеш. факторов влияют только Р и Т, = числу компонентов системы - число фаз + два. Если, кроме Р и Т, условия существования системы определяется еще каким-то перемен. фактором (н-р, φ), то число независ. переменных возрастает на 1: С = К Ф + 3. Если некоторые из параметров состояния системы поддерживаются постоянными, то число независ. переменных уменьшается: С = К Ф + 1 при Р (или Т) = const. C = 0 или целому полож. числу, поэтому Ф равнов. системы можно выразить одной из формул : Ф К, Ф К +1, Ф К + 2. Урав. Гиббса выведено при условии, что каждое из составляющих в-в может беспрепятственно перех. из одной фазы в др. Поэтому оно неприложимо к системам, разделенным полупроницаемыми перегородками.  1. При высоких Т мало изм. с ростом Р в широком интервале Р 2. Площадь под кривой от Р = 0 соответствует величине интеграла 3. При повышении Р для многих газов меняет знак. Поэтому летучесть многих реал. газов сначала < Р, потом = Р, а затем > Р (при бол. Р).Если Т – высокие, Р – невысокие, = const, тогда: lnf = ln P – 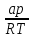 , = f/p = exp (– , = f/p = exp (– 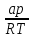 ) ) При мал. и Р функция м.б. разложена в ряд Маклорена (2 члена)  f/p = 1 – f/p = 1 – 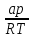 = = 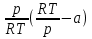 = =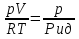 ; ( ; (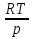 – объем ид. газа; V – объем реал. газа). Здесь Рид – давл., кот-й имел бы ид. газ, если бы он занимал тот же V, кот-й занимает реал. газ . f/p=p/p ид , f = – объем ид. газа; V – объем реал. газа). Здесь Рид – давл., кот-й имел бы ид. газ, если бы он занимал тот же V, кот-й занимает реал. газ . f/p=p/p ид , f = 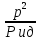 . Это дает возм-ть приближенно вычисл. f при малых Р. Для прибл. вычисления летучестей реал. газов можно воспользоваться методом расчета, основ. на принципе соответственных состояний (ряд одинак. св-в, в том числе и коэфф. акт-ти разл. реал. газов, оказываются равными при одинак. приведенных температурах () и приведенных давлениях (): = Т/Ткр , = Р/Ркр . Это дает возм-ть приближенно вычисл. f при малых Р. Для прибл. вычисления летучестей реал. газов можно воспользоваться методом расчета, основ. на принципе соответственных состояний (ряд одинак. св-в, в том числе и коэфф. акт-ти разл. реал. газов, оказываются равными при одинак. приведенных температурах () и приведенных давлениях (): = Т/Ткр , = Р/Ркр есть универсальная функция и : =f/p=(, ). Эта закономерность – приближенная. На рис.: 2 1 14.2. Диаграммы состояния воды, серы, бензофенона. В однокомп. системах отд. фазы - одно и то же в-во в различных агрегатных состояниях, а если в-во может давать разл. кристал. модификации, то каждая модификация явл. фазой. С = 1 Ф + 2 = 3 Ф, т.е. Ф м.б. = 1, 2, 3. Т.о., ни одно индивидуальное в-во не может образ. равновесн. систему, состоящую более чем из 3 фаз. Диаграмма состояния воды. В уравнение состояния вх. 3 переменные : Т, Р, с (конц.) или Т, Р, V (мольный объем). Любые 2 из них можно рассм. как независ. переменные, а 3ю как их функцию. В больш. случаев Т и Р принимают в кач-ве независ. переменных. Фигуративная - каждая точка на плоскости, кот-я представляет сочетание Т и Р, при кот-я нах-ся система. Линии ОА, ОВ, ОС принадлежат обеим соприкасающимся областям, и каждая т. на этих линиях может отвечать как совместному существованию обеих фаз, так и наличию только одной из фаз. Если переход еще не начинался или уже завершен, то система предст. собой только одну фазу. ОА - кривая возгонки, ОВ кривая плавления, ОС кривая кипения или испарения; заканчивается критич. точкой. OD показывает, как меняется давл. пара над переохлажденной водой. Переход охлаждаемой жидкости в кристал. состояние не всегда начинается точно при Т замерзания. Если жидкость не сод. хотя бы мельчайших тв. частиц, кот-е могут служить центр. кристаллизации, то происх. переохлаждение. –Ц- кристаллизации сопровожд. выдел. Q, поэтому Т системы вновь ↑ и достигает равновесной Т замерзания, при кот-й и протекает весь остальной –ц- кристаллизации. Р пара над переохлажд. жидкостью > Р пара над кристаллами (OD выше ОА). переохлажд. жидкость термодинамически неустойчива по отн. к кристал. фазе, находящейся при той же Т. О тройная точка ; в ней возможно равновесное сосуществование как одновременно всех 3 фаз, так и сосуществование любых 2 фаз и наличие только 1 из фаз.Число степ. свободы в разл. точках : Т. 1 : С1 = 1 1 + 2 = 2. Система бивариантна. При наличии одной фазы можно произвольно (в известных пределах, не переходя границ соответствующей области) менять Р и Т, не изменяя числа фаз. Фигур. т. 1 можно смещать на некоторое расстояние в люб. направлении. Т. 2 : С2 = 1 2 + 2 = 1. Система моновариантна если мы захотим изменить условия существования системы, сохраняя равновесие между двумя фазами (льдом и жидкой водой), то мы можем произвольно изменить лишь один параметр состояния, например, Т. Давление же при этом следует изменить на вполне определ. величину так, чтобы фигур. точка системы (т.2) смещалась строго по кривой ОВ. Т. О : тройная точка (система нонвариантна) : СО = 1 3 + 2 = 0. Равновесное сосуществование трех фаз возможно лишь при единственном сочетании значений Р и Т. Наклон ОА, ОВ, ОС определ. знаком и величиной dP/dT в урав. Клапейрона-Клаузиуса. Знак определ. знаком разности мольных объемов фаз (V2 V1). Кривые возгонки и кипения всегда наклонены вправо; обычно –ц- плавления тоже сопровожд. увеличением мольного V, и ОВ почти у всех в-в наклонена также вправо. В случае воды (а также висмута, чугуна и галлия) мольный V жид. фазы < мольного V тв. фазы, и кривая плавления наклонена влево (только при низких Р). Вблизи тройной точки кривая возгонки всегда обладает более крутым подъемом, чем кривая кипения, т.к. теплота возгонки больше теплоты кипения. Плоская диаграмма состояния однокомп. системы не отражает V системы и изменения V при переходе от одной фазы к другой. Диаграмма состояния серы Кристал. S может сущ. в 2х модификациях ромбич. и моноклинической S образ. 4 фазы: 2 кристал., жидкую и пар; т.о. на диаграмме 4 области. Три тройные точки : А, В, С. Но сущ. еще 1 тройная точка О, в кот-й могут сосуществовать перегретая ромб. S, переохлажденная жидкая S и пересыщенный пар. 3 неравновесные фазы могут образ. метастабильную систему (т.е. в состоянии относит. устойчивости): 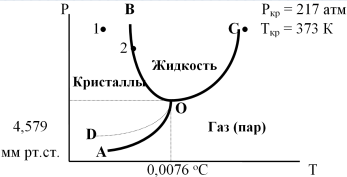 15.1. Уравн. для характер. функций многокомпон. систем, . Урав. Гиббса-Дюгема. Р-р образ-ся из комп-тов самопроив-но. Поэтому его образ-е при Р, Т = const связ. с ↓ G системы. GAGGB показ. зав-ть изобар. потенциала 1 моля р-ра от состава р-ра для 2х жидких компонентов А и В, смешивающихся во всех отношениях. Любая т.G на этой кривой лежит ниже т.G , отвечающей изобар. потенциалу системы, состоящей из компонентов А и В, взятых в тех же кол-вах, что и в р-ре, но не смешанных друг с другом. Если компонент В находится в тв. состоянии, то он будет растворяться в жидкости А до тех пор, пока не образуется насыщ. р-р, в j мольная доля компонента В равна N. GAGGN показ. изменение G р-ра с изменением его состава; т.GN отвечает насыщ. р-ру. 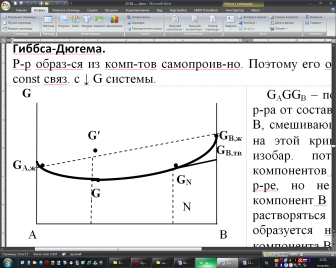 При добавлении тв. компонента В к насыщ. р-ру дальнейшего его растворения не происходит, и система состоит из двух фаз насыщ. р-ра и кристаллов компонента В. Зависимость G этой системы от состава изображается прямой GNGB,тв , где GB,тв G чистого тв. компонента В. Т.о., величина G р-ра - функция не только Р и Т, но и функция m каждого компонента р-ра; это относится ко всем термод. потенциалам и др. экстенсив. св-вам (т.е. св-вам, пропорциональным m). Выражение I закона термодинамики следует расширить: dU=QA+1dn1+2dn2+… ni число молей компонентов раствора, i– коэффициенты пропорциональности между dU и dni Для равновесного процесса при наличии только А расширения : dU = TdS – PdV + idni ; dF = – PdV – SdT + idni Это выражение есть полный дифференциал функции F=F(V,T,ni) i= 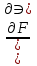 V,T,n (индекс V,T,n (индекс 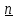 показывает постоянство масс остальных компонентов) показывает постоянство масс остальных компонентов)15.2. Условия хим. равновесия. ЗДМ (вывод, анализ). Разл. формы выражения К равн. Хим. реакции обратимы : наряду с хим. взаимодействием м/у исх. в-вами (прямая реакция) протекает хим. взаимодействие м/у продуктами реакции (обратная реакция), в рез. которого снова образ. исх. в-ва. По мере протекания -ц- скорость прямой реакции (кол-во молекул, прореагировавших за секунду) уменьшается, а скорость обратной реакции увел.. Когда обе скорости сравняются, наступает состояние хим. равновесия число молекул в-в, составляющих хим. систему, перестает меняться и остается постоян. во времени при неизменных внеш. усл.. Хим. равновесие явл. динамичным и подвижным с изменен. внешн. условий равновесие сдвигается в одну или в др. сторону; б/м изменение внешн. условий влечет за собой б/м изменение состояния равновесия. Т.о., хим. реакции могут протекать как равновесные –ц-, т.е. к ним можно применять общие условия термодинамич. равновесия. Изменение G сист., в кот-й протек. хим. р-ция: dG=SdT+VdP+1dn1+2dn2+... Однако в этом случае изменения масс компонентов dn1, dn2 ... не являются независимыми, а связаны стехиометрическими соотношениями :1А1+2А2+...=1А1+2А2+... Изменения масс компонентов, выраженные в молях, пропорциональны стехиомет. коэф. уравнения реакции, взятым с соответств. знаком («» для исчезающих в-в, «+» для образ.) : 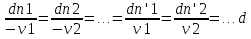 изменения масс исх. в-в изменения масс продуктов реакции изменения масс исх. в-в изменения масс продуктов реакцииОтношение dni/i одинаково для всех участников хим. реакции и м.б. записано в форме дифференциала некоторой величины . хим. переменная : показывает m каждого компонента, вступившую к данному моменту в реакцию и измеренную в эквивалентных единицах, отвечающих уравнению реакции. характеризует только одну определ. хим. реакцию. Если в системе протекает несколько реакций, то для каждой из них имеется своя переменная (1 , 2 ...). dG=VdPSdT11d22d...+11d+22d+...=VdPSdT+(ii)d Здесь G=G (P,T,) , 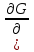 ) p,T = ii ) p,T = iiЧаст. произв. G по =алгеб. произведений ii . При P,T=const: (G)P,T=(ii)d Для реакций, протекающих самопроизв. при P,T=const , dG 0(ii)0 , т.к. d 0. Когда реакция находится в состоянии равновесия, функция G = f () имеет min значение : 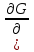 )p,T = ii = 0условие хим. равновесия (в общей форме). )p,T = ii = 0условие хим. равновесия (в общей форме).Аналогично: 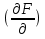 v,T = ii = 0 в состоянии равновесия. v,T = ii = 0 в состоянии равновесия.16.1.Давление нас. пара бинарных р-ров. Закон Рауля. Ид. растворы. Предельно разбавл. р-ры. Насыщ. пар содержит, в общ. случае, все компоненты р-ра, и Р насыщ. пара = парц. Р компонентов. Но часто отд. компоненты нелетучи при данной Т и отсут. в газ. фазе. Полное Р нас. пара и парц. Р явл. функциями Т и состава р-ра. При Т = const состояние бин. р-ра определ-ся лишь конц.1 из компонентов. Диаграмма Р – состав для р-ра 2х жидкостей, смешивающихся во всех отношениях. РоА и РоВ – Р пара чистых жидкостей. Состав насыщ. пара определяется мольной долей 2-го компонента: N2 = Р2 / Р (Р2 – парц. давление 2-го компонента, Р – полное давление пара). Если насыщ. парид. газ, то для компонентов пара:i=Gi(T)+RTlnpi; 2=G2(T)+RTlnp2 Т.к. хим. потенциалы компонента в равновесных фазах равны, то это уравнение имеет силу и для жидкого раствора.  Для чистого жидкого 2-го компонента при той же Т: о2=Gо2(T)+RTlnРо2 ; Получаем: 2=о2(T)+RTln(p2/p20) При высоких Т и Р нас. пар р-ра не явл. ид. газом: 2 = о2(T) + RTln (f2 / f20); f2 – парциальная летучесть 2-го компонента в р-ре; f o2 – летучесть 2го компон. в виде чистой жидкости при той же Т. ЗАКОН РАУЛЯ. В простейшем случае зав-ть парц. Р пара р-ля от состава бинарного р-ра: Р1 = Ро1 N1 = Po1 (1 – N2 ) = Po1 (1 – N) Т.е. изображается на диаграмме P – N прямой линией. З. Рауля : относительное понижение парц. Р пара р-ля = N раствор. в-ва N = ( P10 – P1) / P10 (1) Закон применим к р-рам, нас. пар кот-о ведет себя как ид. газ. Немногие р-ры подчиняются этому закону. Пока Р нас. пара невелико, отклонения от з. Рауля малы. При высоких Т, когда Р нас. пара велико, термодинам. св-ва газов нужно связывать с летучестями и з. Рауля выражать в след. форме: f1=f о1 N1=f o1(1–N) ; N= 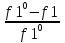 (2) (2)Р-ры, следующие з. Рауля в форме урав. (2) при всех конц. и всех Т, наз-ся идеальными (совершенными) р-рами; это предельный, простейший тип жидких р-ров. Для пара раствор. в-ва должно соблюд. урав., аналогичное вышеприведенному. Из уравнений (2) получаем: df1 = f o1 d (1 – N ) = – f o1 dN и подставляем в уравнение Дюгема-Маргулеса: d ln f2 = – 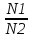 d ln f1 = – d ln f1 = – 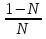 d ln f1 = – d ln f1 = – 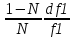 = = 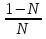 ; ; 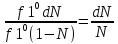 d ln f2 = 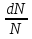 ; ln f2 = ln N + ln k ; f2 = kN (3) ; ln f2 = ln N + ln k ; f2 = kN (3) Если р-р ид., то (3) справедливо для всех конц. |
