Шпоры по физхимии. 1 Энергия, теплота, работа. Первый зн термодинамики. Внутренняя энергия и энтальпия фи состояния системы
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
|
8.1. Вычисление энтропии. Постулат Планка. Уравнения, определяющие энтропию, являются единст. исходными уравнениями для т/д расчета изменений системы: 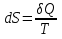 ; ; 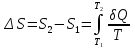 1. Изменение энтропии при поглощении Q при пост. Т и Р( или V): 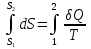 ; ; 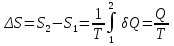 => => 2. Изменение энтропии при нагревании(охлаждении) в-ва от Т1 до Т2 при постоянном P и V: 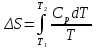 ; Надо знать зависимость СР от Т. Допустим: ; Надо знать зависимость СР от Т. Допустим: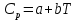 : : 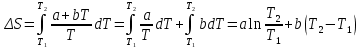 3. Изменение энтропии для разл. процессов с ид. газом: 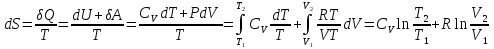 Если Cv = const, то 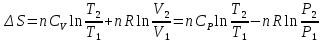 В изотермическом, учитывая, что Т1=Т2= const, 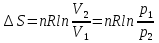 В изохорном 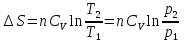 В изобарном 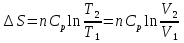 4. Изменение энтропии при взаимной диффузии 2х ид. Газов (р и Т одинаковы) 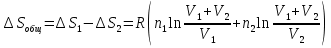 Учитывая, что 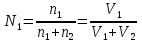 и и 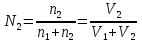 Где Ni- молярная доля газа в полученной газовой смеси, получим выражение для расчета изменения энтропии при взаимной диффузии двух идеальных газов: 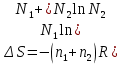 8.2. Применение 3-го закона для расчета хим. равновесий. Приближение Улиха. Метод Темкина – Шварцмана. Прямой и простой расчет G р-ий и КР возможен, если известны абс.энтропии всех участников р-ии. Для р-ий, протекающих при Т = const: GTo =HTo–TSTo (HTo – теплота реакции при Р = const , STo изменение S при превращении чистых исх. в-в, взятых в станд. состоянии при Р = 1 атм, в конечные в-а в том же состоянии: So =iSio Если для данной Т известны Q реакции Но и энтропии Sio всех участников р-ии, то расчет Go – элемент. арифм. операция. Если известны CP = f(T), можно вычислить Но при данной Т по уравнению Кирхгоффа и S каждого участника по уравнению : 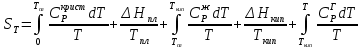 а затем найти Go. Т.о., изложенный метод расчета хим. равновесий базируется на постулате Планка. Однако для обоснования метода расчета достаточно утверждение, что изменение энтропии для всех процессов (в том числе и хим. р-ий), происходящих при Т = 0 с участием только кристалл. чистых в-в, =нулю. Действительно: 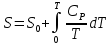 . Изменение S при хим. р-ии составляет: . Изменение S при хим. р-ии составляет: 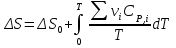 . Приняв So = 0, получим: . Приняв So = 0, получим: 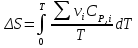 , т.е. возможность вычислить S, используя те же табличны величины стандартных энтропий. , т.е. возможность вычислить S, используя те же табличны величины стандартных энтропий.Уравнение So = 0 является выражением теплового закона Нернста, который был исторически первой формой 3 з-на т/д. Изложенный метод расчета хим. равновесий наз-ся методом абсолютных энтропий и является общим для р-ий в любых системах. Он позволяет использовать эмпирические уравнения. 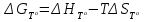 ; ; 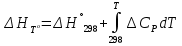 ; ; 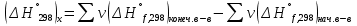 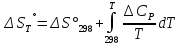 ; ; 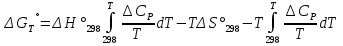 – уравнение для точного расчета G реакции; надо знать : So298 и СР(Т). – уравнение для точного расчета G реакции; надо знать : So298 и СР(Т).9.1. Энергия Гельмгольца F и энергия Гиббса G. Энтропиякритерий оценки направления процесса (самопроизвольного протекания процесса) и достижения равновесия в изолир. системах. Для разбора изотерм. процессов нужно применять другие критерии. Изохорно-изотермический потенциал (Изохорный потенциал, свободная энергия, энергия Гельмгольца) Q=dU+ATdS; ATdSdU; пусть T=const; AT(S2S1)(U2U1), A(U1TS1)(U2TS2); UTS=F, F=U-TS; Fсвоб. энергия системы; Fф-я состояния системы, т.к. U, T, S тоже ф-ии. AF1F2 ; AF. В равновесных процессах A=F (равна убыли F) А равновесного процесса (макс. А) не зависит от пути, а определяется лишь нач. и конеч. состояниями системы. U=F+TS U состоит из 2х частей свободной энергии F и связанной энергии TS : лишь часть U (F, система отдает вовне при T = const) может превратиться в A. Другая часть U связанная энергия при изменении системы при T = const не дает A, а переходит только в Q :TS = K ;dK= TdS + SdT ; SdT = 0; dK= TdS ; K = TS = Q Для процессов, прот-щих с изменением Т деление «U» на свободную и связанную не м. б. проведено. Изохорный потенциал есть функция V и Т :
dF=–PdV–SdT , F= F(V,T)– это полный дифференциал ф-ии от V,T. dF = 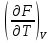 dV + dV + 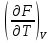 dT ; dT ;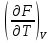 = – P , = = – P , =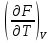 – S; – S; P – мера убыли F с ростом V при T= const S – мера убыли F с ростом Т при V = const
dUTdS–A , dFTdS–PdV–TdS–SdT; dF–PdV–SdT Если V = const и T = const и отсутствуют др. виды А : (F)V,T0 т.е. F системы, наход-ся при V,T = const, не изменяется при равновесных процессах и убывает при неравнов. процессах T T B b(1) с(1) A X0 X1 Крист. А + Крист. В w(1) p(2) h(2) r(1) g(1) a(1) k(2,3,2) l(1,3,2) b(1,2,1) tA tB v n u tЭ Расплав +крист. А Расплав +крист. В →вес.%В 9.2 Диаграмма сост. двухкомпонентной системы с простой эвтектикой (бинарные сплавы, растворы солей). В уравнениях сост-я двухкомпонентных систем число переменных =4: Т, Р., С1, С2. Т.о., для построения полной диаг-мы сост-я необходимо располагать сис-мой координат четырех измерений. Подобное построение невозможно, и это вынуждает прибегать к некот. упрощениям. С этой целью переходим к переменным Т, Р., мольному объему и мольной доле 1-го компонента N1 (N2 = 1 N1); вместо мольных долей можно выражать содержание компонентов в весовых %.Выбираем в качестве независимых переменных Т, Р., N1 и строим трехмерную диаграмму в этих координатах. Все прост-во объемной диаграммы разделено поверхностями раздела на обл-ти существования определенных фаз. В практ. работе пользуются упрощенными диаграммами сечениями объемной диаг-мы плоскостями, отвечающими P = const или T = const. (Неизоморфная смесь, компоненты которой не образуют хим. соединения и совершенно нерастворимы в тв. состоянии) При кристаллизации двухком-ого расплава выделяются только чистые кристаллы каждого из компонентов (пример система Cd-Bi).Проследим за процессом крист. этой системы при Р = const на примере расплавов различного состава. p=const Точка а: одна фаза жидкий компонент А. Число фаз не меняется, пока не будет достигнута темп-ра кристалл. tA (d). В момент достижения этой темп-ры налицо одна жидкая фаза; при дальнейшем отнятии Q появится 2ая фаза кристаллы А. Весь процесс кристалл. чистого в-ва протекает при tA = const, фигурат. точка системы не смещается. Пока идет превращение, С = 1 2 + 1 = 0. По окончании кристаллизации фигурат. точке снова отвечает твердая фаза. Т.о., число фаз в d меняется так : 1 2 1 Дальнейшее отнятие Q вызывает понижение темп-ры кристаллов, и фигурат. точка опускается. При охлаждении бинарного расплава, отвечающего фигурат. точке b, кристалл. протекает иначе. При охлаждении расплава фигурат. точка доходит до которой расплав оказ-ся предельно насыщ. относительно А и представляет собой только одну фазу. При дальнейшем отнятии Q начинается кристалл. в-ва А. Но выделение кристаллов А изменяет состав остающегося расплава в сторону обогащения его в-вом В, и кристаллы А оказ-ся в равновесии с жидкой фазой уже иного состава, чем в точке g. По мере выделения в-ва А его содержание в расплаве постепенно уменьшается, => темп-ра, необходимая для дальнейшей кристалл., непрерывно понижается. В продолжение всей кристалл. фигурат. точке всей системы отвечают 2 фигурат. точки тв. и жидкой фаз(точке hотвечают точки vи w). Фигурат. точка тв. фазы опускается по вертикали, начиная отn, и доходит до u. Фигурат. точка расплава перемещается по кривой gl. Выделение кристаллов А продолжается до тех пор, пока фигурат точка жидкой фазы не совпадет с l. Расплав этого состава находится в равновесии как с кристаллами А, так и с кристаллами В, а потому при отнятии Q из жидкой фазы одновременно выделяются кристаллы обоих компонентов; состав расплава остается при этом постоянным. 1.Насыщ. пар по сравнению с равновесным р-ом отн-но богаче тем компонентом, добавление кот. к сист-ме повышает полное P пара (т.е. тем, кот-ый более летуч). 2. Повышение относительного содержания данного компонента в жидкой фазе всегда вызывает увеличение его относительного содержания и в парах. Первый закон Коновалова справедлив для всех устойчивых р-ов. Значительные «+» и «-»отклонения растворов от з-на Рауля приводят к появлению макс. или мин. на кривой полного P пара (изобарные диаграммы Ткип – состав имеют обратный вид: макс.общего P соответствует мин.Ткип и наоборот). Второй з-н Коновалова: Экстремумы на кривых полного P пара (или Т кипения) отвечают такому равновесию р-ра и насыщ. пара, при которых составы обеих фаз одинаковы. По 2 з-ну Коновалова, на диаграммах Рпара (или Ткип), имеющих экстремумы, обе кривые – кривая пара и кривая жидкости – должны касаться в точке экстремума. С р-ом, состав кот. отвечает экстремуму, находится в равновесии пар такого же состава. Cостав таких р-ов при перегонке не меняется и они кипят при Т = const. Такие р-ры наз-ся азеотропными (нераздельно-кипящими). Фракционная (дробная) перегонка. Разделение азеотропных растворов. Разделение р-ра на компоненты перегонкой возможно благодаря различию в составах равновесных жидкости и пара. См. рис. диаграммы Ткип – состав: по мере выкипания в жидкой смеси все больше относительное содержание высококипящих компонентов; отгоняемая фракция относительно богаче более летучим компонентом. Повторяя фракционирование, соединяя близкие по составу фракции последовательных перегонок, постепенно увеличиваем массы крайних фракций конденсата и уменьшаем массы средних фракций и в конце концов приходим к чистым компонентам А и В. Разделение раствора на компоненты А и В путем перегонки невозможно, если они образуют азеотропный раствор (при определенном соотношении компонентов). Пусть диаграмма Ткип – состав имеет минимум. Она состоит как бы из двух частей, каждая из которых аналогична диаграмме Ткип – состав без экстремума. Перегонка раствора любого состава приведет к концентрированию в остатке одного из компонентов (А или В); в конденсате – азеотроп. В случае азеотропа с максимумом Ткип ректификация раствора приведет к обратным результатам: азеотроп останется в колбе, а в приемнике соберется чистый компонент. 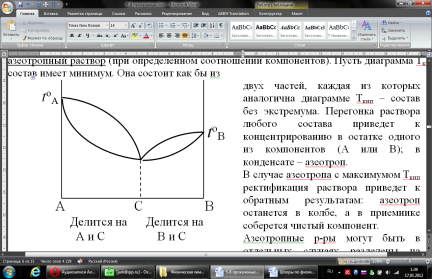 Азеотропные р-ры могут быть в отдельных случаях разделены на чистые ком. Для адиабаты ВС:Т1V2-1=T2V3-1 Для адиабаты AD:T1V1-1=T2V4-1 Разделим эти равенства друг на друга и извлечем корень степени -1 : 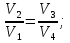 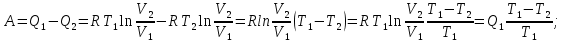 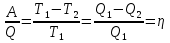 Отношение A/Q1 показывает, какая часть Q, поглощенной газом, превращается в A; оно наз-ся КПД цикла. В данном случае это КПД цикла Карно с ид. газом, рассматриваемого как тепловая машина. Величина КПД () зависит от разности температур, м/у j работает цикл Карно:1. Т1 = Т2 : = 0, А = 0 получение А при Т = const невозможно; Т нагревателя и холодильника д. б. различны; 2. Т2 = 0 : = 1, А = Q1 теоретически полное превращение Q1 в А возможно при холодильнике с Т = 0 К. Теорема Карно-Клаузиуса : КПД тепловой машины, работающей по циклу Карно, не зависит от природы рабочего тела машины, а лишь от T нагревателя и холодильника. Цикл Карно равновесен, т.к. все составляющие его процессы равновесны. *Из I ЗТ и вытекающих из него закономерностей нельзя сделать вывода о том, возможен ли вообще данный процесс и в каком направлении он протекает. II ЗТ накладывает определенные ограничения на взаимные переходы энергии из одного вида в др. Он позволяет предвидеть направление течения процесса и глубину его протекания.Формулировки II закона термодинамики :
Математическое выражение II ЗТ : 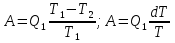 Расплав 1. Т понижается, фигуративная т.1 опускается; т. l отвечает предельному охлаждению, при кот. система еще однофазна. При дальнейшем охлаждении выделяется тв. р-р, состав которого меняется по линии солидуса со; состав равновесного с ним жидкого р-а меняется по линии ликвидуса са. Т.о., например, фигуративной точке всей системы m отвечают точки m” и m’ равновесных жидкого и тв. р-в. По достижении Т, кот. отвечает т. n , система состоит из жидкого р-ра а и тв. р-pа о . Жидкий р-р а может находиться в равновесии одновременно с 2мя тв. р-ми о и р ; он наз-ся жидкой эвтектической смесью. При дальнейшем отнятии Q из эвтектической смеси выделяются 2 тв. р-ра о и р . Во время кристаллизации эвтектики имеются 3 фазы : расплав а , кристаллы р и кристаллы о . После окончания кристаллизации остаются 2 кристаллические фазы, каждая из кот. представляет тв. р-р. При дальнейшем охлаждении смеси тв. р-ов состав этих р-ов изменяется; так, точке q отвечает смесь тв. р-ов r и s . Расплав 2. Система однофазна до т. f включительно. При дальнейшем охлаждении образуются 2 фазы, подобно предыдущему случаю. При Т точки t весь расплав затвердевает, и снова имеется одна равновесная фаза. Теперь это тв. р-р того же состава, что и исх. жидкий р-р. Тв. р-р при дальнейшем охлаждении не изменяется, пока не будет достигнута Т его предельного охлаждения т. и . При более низких Т происходит разрыв сплошности тв. фазы, и система А-В снова оказывается двухфазной, т.е. представляет собой тонкую смесь кристаллов тв. р-ов 2x типов А в В и В в А. Изменение энтропии, рассчитываемое по этому уравнению, всегда положительно, так как все lnNi<0, поэтому идеальные газы смешиваются необратимо. Если при тех же условиях вмешиваются 2 порции одного и того же газа, то это уравнение уже неприменимо, но эта формула не содержит никаких индивидуальных параметров газов, это противоречие называют парадоксом Гиббса. По этим уравнениям невозможно вычислить абс. значение энтропии. Такую возможность дает недоказуемое положение, не вытекающее из двух законов термодинамики, сформулированное Планком (1912). Постулат Планка: энтропия индивид. кристаллического в-ва при абс. нуле = нулю : So = 0. 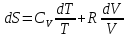 ; ; 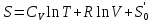 ; ; 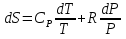 ; ; 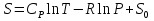 Постулат используется для вычисления абс. значений энтропий хим.соединений величин, которые имеют большое значение при расчете хим. равновесий. Строго говоря, постулат справедлив только для индивидуальных веществ, кристаллы которых идеально построены.
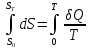 ; ; 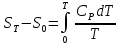 ; ; 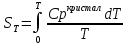 Для расчета величины ST надо знать зависимость СР от Т, причем опред. до возможно более низких Т (до 10 К или, в крайнем случае, до 80 К). Значение СР при 0 К находят путем экстраполяции или с помощью эмпирических приемов.
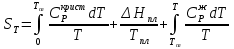
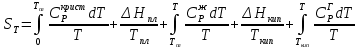 можно вычислить энтропию реального газа при температуре Т и Р = 1 атм (если испарение проводилось при нормальной Т кипения). Когда вещество в твердом состоянии имеет несколько модификаций, в уравнения добавятся соответствующие члены (нагревание и фазовый переход). Интегральные члены уравнения находят графическим интегрированием : строят кривые СР/Т = f (Т) и значение интеграла находят по площади. Абс. значения энтропии, рассчитанные для стандартных условий (Р = 1 атм, Т = 298 К), называются стандартными значениями энтропии So298. Такие р-ции зависят от Р (для идеальных газов), и с ростом Р, (в соответствии с законом смещения равновесия) равновесие сдвигается влево. Этим реакции, протекающие с изменением числа молекул, отличаются от реакций, рассмотренных ранее. Найдем связь между КР , Кс , КN для этой р-ии : КР=Кс(RT)=Kc RT; =1; KP=KN P=KN P Рассмотрим еще один тип реакций, для которых =1: 2CO2 2CO+O2 ( 2SO32SO2+O2;2H2O2H2+O2) 2 (1) 2 числа молей веществ в состоянии равновесия; no = 2. Выразим через КР реакций этого типа. n=22+2+=2+ 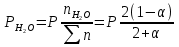 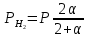 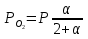 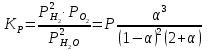 Это кубическое ур-ие относительно . Если очень мала (для водяного пара это имеет место при Т 1500оС), то ею можно пренебречь в скобках в знаменателе: КР = Р α3/2 Влияние Р на незначительно : при увеличении Р в 10 раз уменьшается в 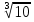 = 2,15 раза. = 2,15 раза.К этому же типу принадлежит реакция контактного получения серного ангидрида : 2SO2 +O2 2SO3 КР в данном случае можно выразить с помощью степени превращения сернистого газа. Степень превращения равна доле исходного количества вещества (SO2),вступившего в реакцию. Чем больше , тем полнее протекает реакция. Введем обозначения : no исходное число молей SO2, no a исходное число молей О2, степень превращения. В равновесии : nSO2 = no (1 ), nO2 = no (а β/2) , nSO3 = no , n = no no +no ano β/2+no =no(1+a β/2); 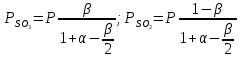 ; ; 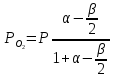 ; ; 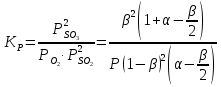 Опытные и вычисленные значения КР практически совпадают. Видно уменьшение , т.е. выхода SO3 , по мере уменьшения относительного количества O2. Можно теоретически показать, что максимальный выход всегда получается из стехиометрической смеси, в данном случае 2SO2 + O2 . К иному стехиометрическому типу относится неорг. синтез : 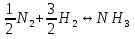 За протеканием реакции удобно следить, измеряя мольную долю N аммиака в равновесной смеси. Если при синтезе NH3 берется стехиометрическая смесь H2 и N2, то в состоянии равновесия мольные доли компонентов будут составлять:– За протеканием реакции удобно следить, измеряя мольную долю N аммиака в равновесной смеси. Если при синтезе NH3 берется стехиометрическая смесь H2 и N2, то в состоянии равновесия мольные доли компонентов будут составлять:–NNH3=N, NH2=3/4(1N), NN2=1/4(1N) 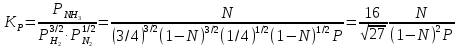 N и КР увеличивается с ростом Р. КР ≠ const вследствие увеличивающегося с ростом Р отклонения газовой смеси от идеал. сост. В этих условиях константой является Кf , равная КР при малых Р. Рассмот. примеры газовых равновесий показывают, что вид выражений для Кравн изменяется в зависимости от стехиометрического типа реакции и величины, выбранной для характеристики процесса (α , β , N и т.д.). 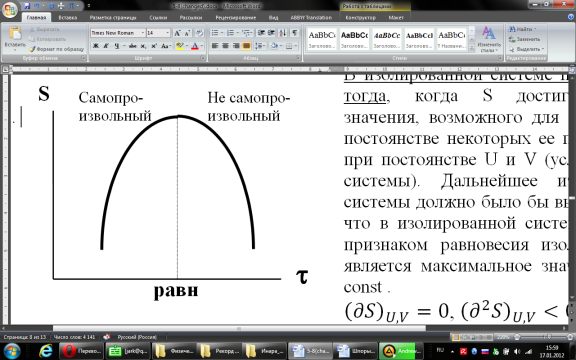 В изолированной системе процессы прекратятся тогда, когда S достигнет максимального значения, возможного для данной системы при постоянстве некоторых ее параметров, а именно при постоянстве U и V (условия изолированной системы). Дальнейшее изменение состояния системы должно было бы вызвать уменьшение S, что в изолированной системе невозможно. Т.о., признаком равновесия изолированной системы является максимальное значение S при U, V = const . 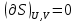 , , 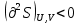 условие равновесия в изолированной системе. условие равновесия в изолированной системе.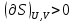 условие самопроизвольного протекания процесса в изолированной системе условие самопроизвольного протекания процесса в изолированной системеВ системе, обменивающейся теплотой и работой с окружающей средой, возможны процессы, сопровождающиеся как возрастанием, так и убыванием S. решения вопроса о направлении процесса следует включить в систему все тела, Поэтому для участвующие в процессе, и т.о. сделать систему изолированной. Расплавы, которые могут быть в равновесии с кристаллами обоих компонентов, называются жидкой эвтектической смесью или жидкой эвтектикой, а Т ее кристаллизации эвтектической точкой. Жидкая эвтектика в процессе кристалл. переходит в твердую эвтектику. Вследствие постоянства состава жидкой фазы кристаллизация эвтектической смеси протекает при постоянной Т, подобно кристаллизации индивид. в-ва. Когда фигурат. точка всей системы достигает положения k, система состоит из 2x фаз кристаллов А и жидкой эвтектики. В процессе кристалл. жидкой эвтектики система состоит из 3x фаз: расплава, крист. А (как выделившихся раньше, так и образующихся при кристалл. эвтектики) и крист. В, выделяющихся из жидкой эвтектики. По окончании кристалл. система состоит из 2x кристалл. фаз, j и сохраняются при дальнейшем охлаждении. Если в исх. расплаве имеется избыток в-ва В, то в процессе охлаждения в первую очередь происходит выделение крист. В (кривая tBl начало кристалл.), и расплав обогащается в-вом А. Порядок изменения числа фаз при этом тот же, что и в описанном выше примере кристалл. в-ва А. При охлаждении расплава, состав j в точности отвечает составу эвтектики (точка с), кристалл. начинается в точке l без предварительного выделения 1го из компонентов. При Т, отвечающей этой точке (tЭ), система проходит последовательно 3 состояния:1 фаза расплав, 3 фазы расплав и 2 вида крист., 2 фазы 2 вида кристаллов (тв. эвтектика).При Т более низких, чем tЭ, система состоит из 2x кристалл. фаз. Фигурат. точки, выражающие составы 2x равновесных фаз, наз. сопряженными точками, например точки v иw, а кривые, образованные рядами этих точек, сопряженными кривыми (линииdlиdu). Линии, соединяющие сопряженные точки, наз. нодами или коннодами (линияvw). Согласно правилу рычага, фигурат. точка всей системы (точкаh) делит проходящую через нее ноду (ноду vw) на отрезки, обратно пропорциональные массам фаз, на которые распадается равновесная система: 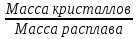 = = 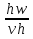 Число степеней свободы в разных точках: Число степеней свободы в разных точках:т. b(c) С = 2 1 + 1 = 2 т.е. система остается однофазной при произвольном одновременном изменении Т и содержания одного из компонентов. т. g(r)С = 2 1 + 1 = 2 аналогично т. b(c) ; разница в том, что Т и %-ное содержание 1го из компонентов можно изменять только в одну сторону, т.к. эти точки пограничные. т. h(p)С = 2 2 + 1 = 1 т.е. для сохранения двух фаз допустимо изменять произвольно либо только Т, либо только %-ное содержание одного из компонентов расплава, т.к. каждой Т отвечает строго определенный состав раствора, равновесного с кристаллами. т. l(k) С = 2 3 + 1 = 0; аналогично для любой точки, лежащей на линии эвтектики. 3 макс. число фаз; возможно различное сочетание равновесных фаз: расплав + одна кристаллическая фаза, расплав + две кристаллические фазы, две кристаллические фазы. В точке эвтектики возможна и одна фаза. Если взяты расплавы, отличающиеся по составу, то кристаллизация начнется при различных Т, однако закончится она независимо от состава исходной смеси при одной и той же Т: последняя капля жидкости будет отвердевать при tЭ. Если же нагревать твердые смеси различных составов, то конец плавления будет наблюдаться при различных Т, однако плавление начнется при tЭ, причем жидкая фаза будет иметь состав эвтектики. Т.о., понятия Т плавления и Т кристаллизации будут синонимами только для чистых компонентов и эвтектической смеси. Иначе: F системы, наход-ся при V,T=const, стремится у-ся в естеств. (самопр-ных) процессах; когда он достигнет мин. значения, система приходит в равновесие. (F)V,T 0 – критерий направления процесса в системе, находящейся при T,V = const; (F)V,T = 0, ( 2F)V,T 0– критерий равновесия. Все справедливо, если нет других видов A, кроме A расширения. (Изобарный потенциал, энергия Гиббса, свободная энергия при постоянном давлении) Желая учесть в общей форме другие виды A, кроме A расширения, представим элем. A как сумму A расширения и др. видовA A = PdV + A (A – полезная A; А – элементарная полезная A). Q=dU+PdV+A dS. В общем случае (с учетом и равновесных, и неравновесных процессов): A TdS–PdV–dU; T=const, P=const; A T(S2–S1)–P(V2–V1)–(U2–U1)A(U1 –TS1+PV1)–(U2–TS2 + PV2) U –TS + PV =G – энергия Гиббса, ф-ия состояния системы. G = U – TS + PV = F + PV = H – TS ; G =H – TS; A G1 – G2, A – G, Для равн-ных процессов Amax =G максимальная полезная A при изобарно-изотермических процессах равна убыли изобарного потенциала и не зависит от пути процесса.G – та часть Н, которая переходит в полезную работу при P,T = const G = F + PV , – G = – F – PV , A = A – PV Максимальная полезная A равна общей максимальной A за вычетом A изобарного расширения. G – функция Р и Т :G = F + PV, dG = dF + PdV+VdP; dF=–PdV–SdT; dG=–PdV–SdT+PdV+VdP; dG=VdP–SdT , G=G(P,T) dG = 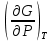 dP + dP + 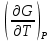 dT ; dT ;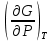 = V , = V , 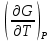 = – S; = – S;V – мера прироста G с ростом Р при T = const S – мера убыли G с ростом Т при P = const.С учетом неравновесных процессов:dG VdP – SdT.Если P,T = const (G)P,T 0; G системы при P,T = const уменьшается при неравновесных процессах и постоянен при равновесных процессах; равновесное состояние системы соответствует минимуму G. (G)P,T 0 – критерий самопроизвольного протекания процесса в системе, находящейся при P,T = const;(G)P,T = 0 , ( 2G)P,T 0 – критерий равновесия в системе. Расчет точного значения GTo по этому уравнению при высоких Т часто невозможен из-за отсутствия Соответствующих экспериментальных данных. В таких случаях возможно применение приближенных методов расчета изобарных потенциалов. Первое приближение Улиха: СР = 0–применяется, когда СР некоторых участн. р-ии совершенно неизвестны. Получаем: GTo=Hо298–TSо298– в пределах Т не более 600 К дает удовлетворительные результаты. Второе приближение Улиха:СР=const–если числ. значения СР у-ков р-ии известны при комнатной Т. 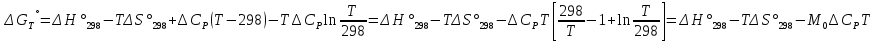 Значения Мо при различных Т сведены в таблицу. Метод Темкина-Шварцмана расчета Go : CP = a+ bT+ cT2+…+ nTn; GTo=Hо298–TSо298–T ( aMo+ bM1+ cM2+ … + nMn); 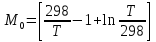 ; ; 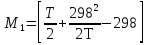 ; ; 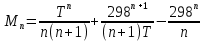 Выражение для Mn справедливо и для n = – 2. Коэффициенты Мо, М1 … уравнения зависят только от Т; они сведены в таблицу для разных Т. Отсутствие значений Sо298 многих в-в (огромного большинства из них) приводит к необходимости пользоваться некоторыми приближенными закономерностями для их подсчета. 10.1. Характеристические функции. Критерии направления процесса и равновесия. ИЗОХОРНО-ИЗОТЕРМИЧЕСКИЙ ПОТЕНЦИАЛ (Изохорный потенциал, свободная энергия, энергия Гельмгольца) U TS = F F = U - TS; не зависит от пути, а определяется лишь нач. и конеч. состояниями системы. U = F + TS Изохорный потенциал есть ф-ия V и Т: 1. Равновесные процессы: F=U–TS; dF=dU–TdS–SdT ,dU=TdS–A; dF=TdS–A–TdS–SdT dF = – PdV – SdT , F = F(V,T)– это полный дифференциал функции от V,T. dF= 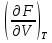 dV + dV + 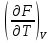 dT ; dT ; 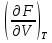 =–P , =–P , 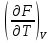 = –S; P–мера убыли F с ростом V при T=const = –S; P–мера убыли F с ростом V при T=constS – мера убыли F с ростом Т при V = const 2. Неравновесные процессы dU TdS – A , dF TdS – PdV – TdS – SdT;dF – PdV – SdT Если V = const и T = const и отсутствуют другие виды А: (F)V,T 0, т.е. F системы, находящейся при V,T = const, не изменяется при равновесных процессах и убывает при неравновесных процессах. Иначе: F системы, находящейся при V, T=const, стремится у-ся в естеств. (самопроизвольных) процессах; когда он достигнет мин. значения, система приходит в равновесие. (F)V,T 0 – критерий направления процесса в системе, находящейся при T,V = const; (F)V,T = 0, ( 2F)V,T 0 – критерий равновесия. Все вышесказанное справедливо, если нет других видов A, кроме A расширения. (Изобарный потенциал, энергия Гиббса, свободная энергия при постоянном давлении) |
