Линейное программирование. Подготовка к зачёту. часть 1.ЛП. 1. методы решения задач линейного программирования
 Скачать 1.44 Mb. Скачать 1.44 Mb.
|
|
На рисунке 1.3 видно, что найденные неотрицательные отношения порождают точки пересечения па положительной полуоси х1. Отношения, соответствующие переменным s3 и s4, исключаются из рассмотрения, поскольку для них точка пересечения или лежит на отрицательной полуоси (s3), или отсутствует (s4). 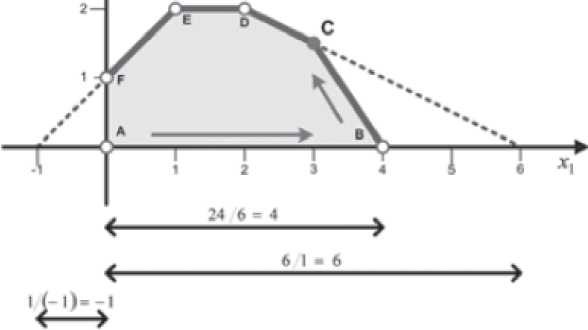 Рисунок 1.3 – Графическая интерпретация отношений как точек пересечения Минимальное неотрицательное отношение соответствует базисной переменной s1. Это определяет переменную s1 как исключаемую, и на следующей итерации ее значение будет равно нулю. Значений вводимой переменной равно минимальному неотрицательному отношению х1=4 (точка В на рисунке 1.3). При этом значение целевой функции возрастёт до 20. Замена исключаемой переменной s1 на вводимую переменную х1 приводит к новым множествам базисных и небазисных переменных и новому решению в точке В. Небазисные (нулевые) переменные: ( s1, x2). Базисные переменные: ( х1, s 2,s3, s4). Теперь необходимо выполнить преобразования в первой симплекс-таблице так, чтобы в столбцах «Базис» и «Решения» получить новое решение, соответствующее точке В. Определим ведущий столбец, ассоциируемый с вводимой переменной, и ведущую строку, ассоциируемую с исключаемой переменной. Элемент, находящийся на пересечении ведущего столбца и ведущей строки, назовем ведущим элементом (таблица 1.4). Таблица 1.4 – Модифицированная первая симплекс-таблица
Процесс вычисления нового базисного решения состоит из двух этапов. 1. Вычисление элементов новой ведущей строки:
Вычисление элементов остальных строк, включая Z -строку: Элемент новой строки = =Элемент текущей строки – (её коэффициент в ведущем столбце)*(новая ведущая строка). В рассматриваемом примере выполняем такие вычисления:
|
