Линейное программирование. Подготовка к зачёту. часть 1.ЛП. 1. методы решения задач линейного программирования
 Скачать 1.44 Mb. Скачать 1.44 Mb.
|
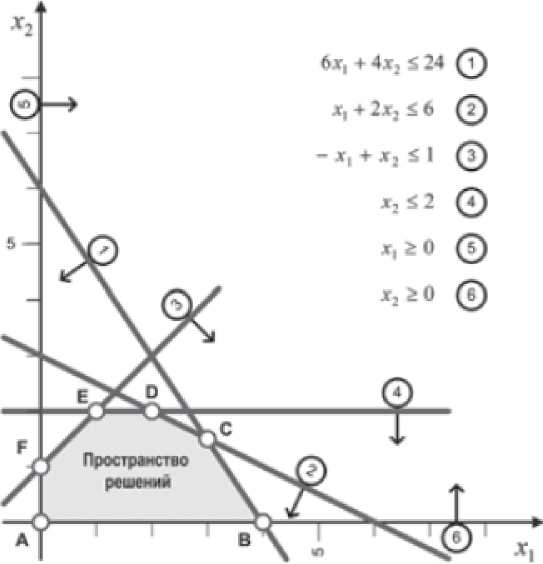
1.3 Геометрический метод решения задачи линейного программированияГеометрический или графический способ решения задачи линейного программирования состоит из двух этапов: 1 Построение области допустимых решений (ОДР), удовлетворяющей всем ограничениям модели. 2 Поиск оптимального решения среди всех точек пространства допустимых решений. Этап 1. Построение пространства допустимых решений Проведем оси координат. На горизонтальной оси будут указываться значения переменной х1, а на вертикальной – х2 (рисунок 1.1). Условия неотрицательности переменных х1≥0, х2≥0 показывают, что пространство допустимых решений будет лежать в первом квадранте (т. с. выше оси х1 и правее оси х2). Учтём оставшиеся ограничения, заменив неравенства на равенства и получив уравнения прямых. Например, неравенство 6х1 + 4х2 ≤24 заменяется уравнением прямой 6х1 + 4х2 = 24. Найдём две различные точки, лежащие на этой прямой, при х1 =0, х2=6. Аналогично для х2 = 0, x1=4. Проведем искомую прямую через найденные точки (линия 1 на рисунке 1.1).
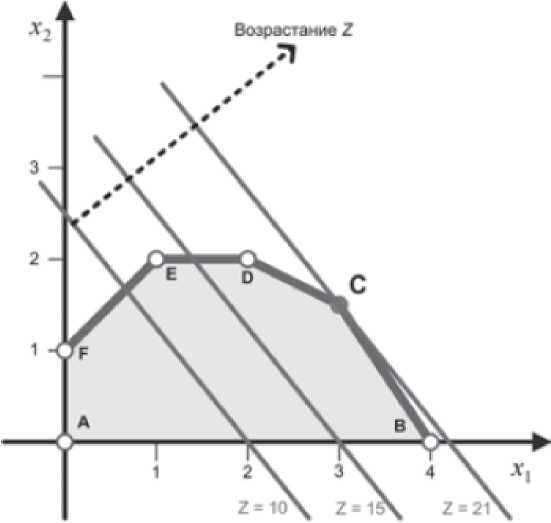
Теперь рассмотрим, как графически интерпретируются неравенства. Точки плоскости, расположенные по одну сторону прямой, удовлетворяют неравенству (допустимое полупространство), а точки, лежащие по другую сторону, нет. Тестовой точкой, может служить точка (0,0). Например, эта точка удовлетворяет первому неравенству: 6х1 + 4х2 ≤24. Это означает, что точки полупространства, содержащего начальную точку (0,0), удовлетворяют этому неравенству. На рисунке 1.1 допустимые полупространства показаны стрелочками. Если точка (0,0) не удовлетворяет неравенству, допустимым полупространством будет то, которое не содержит эту точку. Если же прямая проходит через эту точку, следует в качестве тестовой взять другую точку. Этап 2. Поиск оптимального решения Точки пространства допустимых решений, показанного на рисунке 1.1, удовлетворяют одновременно всем ограничениям. Это пространство ограничено отрезками прямых, которые соединяются в yгловых точках А, В, С, D, Е и F, Любая точка, расположенная внутри или на границе области, ограниченной ломаной ABCDEF, является допустимым решением, т е. удовлетворяет всем ограничениям. Поскольку пространство допустимых решений содержит бесконечное число точек, необходима некая Процедура поиска оптимального решения. Для того чтобы найти оптимальное решение, необходимо определить направление возрастания целевой функции: Z = 5х1 + 4х2. Мы можем приравнять Z к нескольким возрастающим значениям, например, 10 и 15. Получаем уравнения прямых: 5х1 + 4х2 = 10 и 5х1 + 4х2 = 15. На рисунке 1.2 эти прямые показаны штриховыми линиями. Направление возрастания целевой функции отмечено жирной стрелкой. Целевая функция может возрастать до тех пор. пока прямые, соответствующие возрастающим значениям этой функции, пересекают область допустимых решений. Точка пересечения области допустимых решений и прямой, соответствующей максимально возможному значению целевой функции, и будет точкой оптимума.
Оптимальное решение соответствует точке С. Её координаты х1 =3, х2 = 1.5 являются решением рассматриваемой задачи линейного программирования. При этом значение целевой функции равно: Z = 5*3 + 4*1.5=21. Полученное решение означает, что для компании «Российские краски» оптимальным выбором будет ежедневное производство 3 тонн краски для наружных работ и 1,5 тонн краски для внутренних работ с ежедневным доходом в 21000 у. е. |