Линейное программирование. Подготовка к зачёту. часть 1.ЛП. 1. методы решения задач линейного программирования
 Скачать 1.44 Mb. Скачать 1.44 Mb.
|
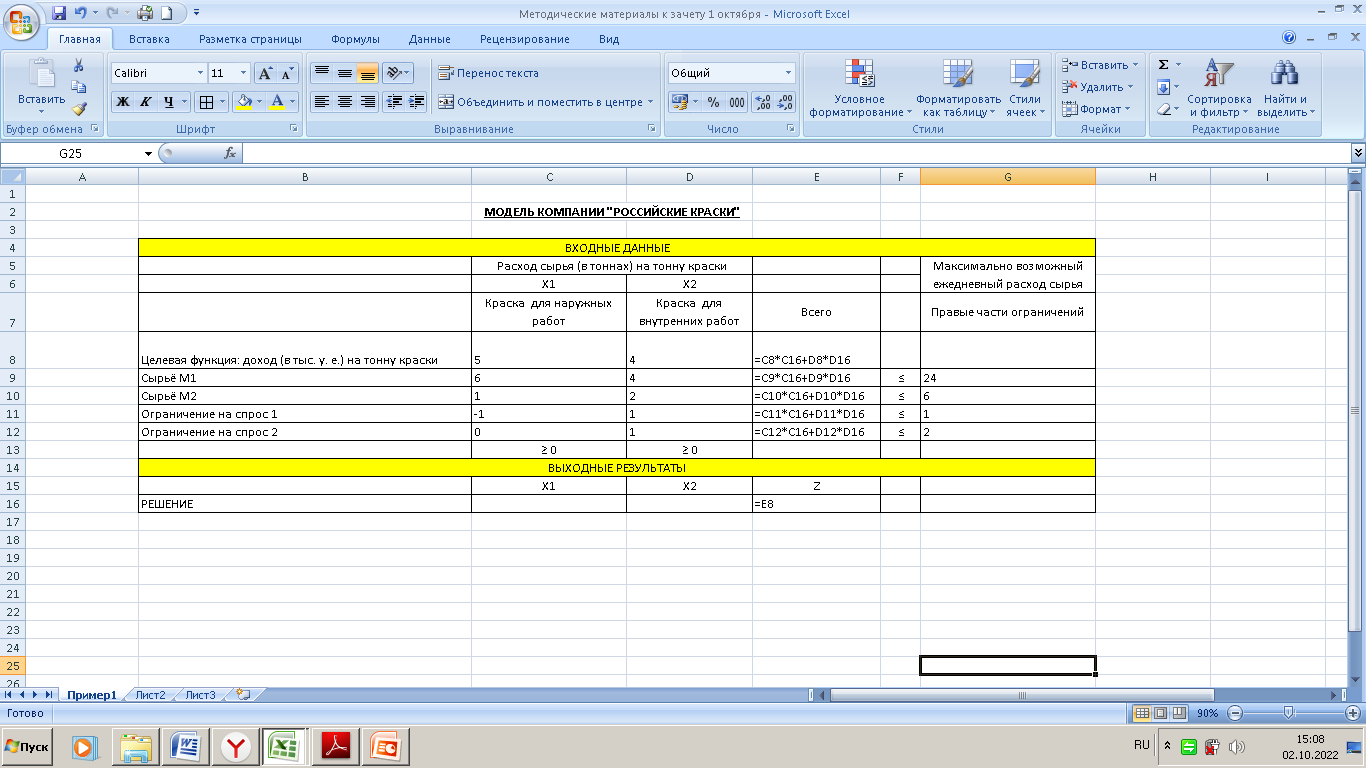
1.5 Использование среды MS Excel для нахождения оптимального допустимого решения задачи линейного программированияhttps://exceltable.com/vozmojnosti-excel/nadstroyka-poisk-resheniya Решение задачи линейного программирования может быть найдено в Microsoft Excel (MS Excel) с помощью инструмента Поиск решения. Расположим исходные данные на листе MS Excel, например, как на рисунке 1.4. Здесь содержится 4 типа данных: поясняющие заголовки и надписи; входные данные (ячейки С8:D12 и G9:G12); значения переменных и целевой функции (ячейки в прямоугольнике C16:E16); формулы, по которым вычисляются значения целевой функции и левых частей ограничений (ячейки G9:G12).
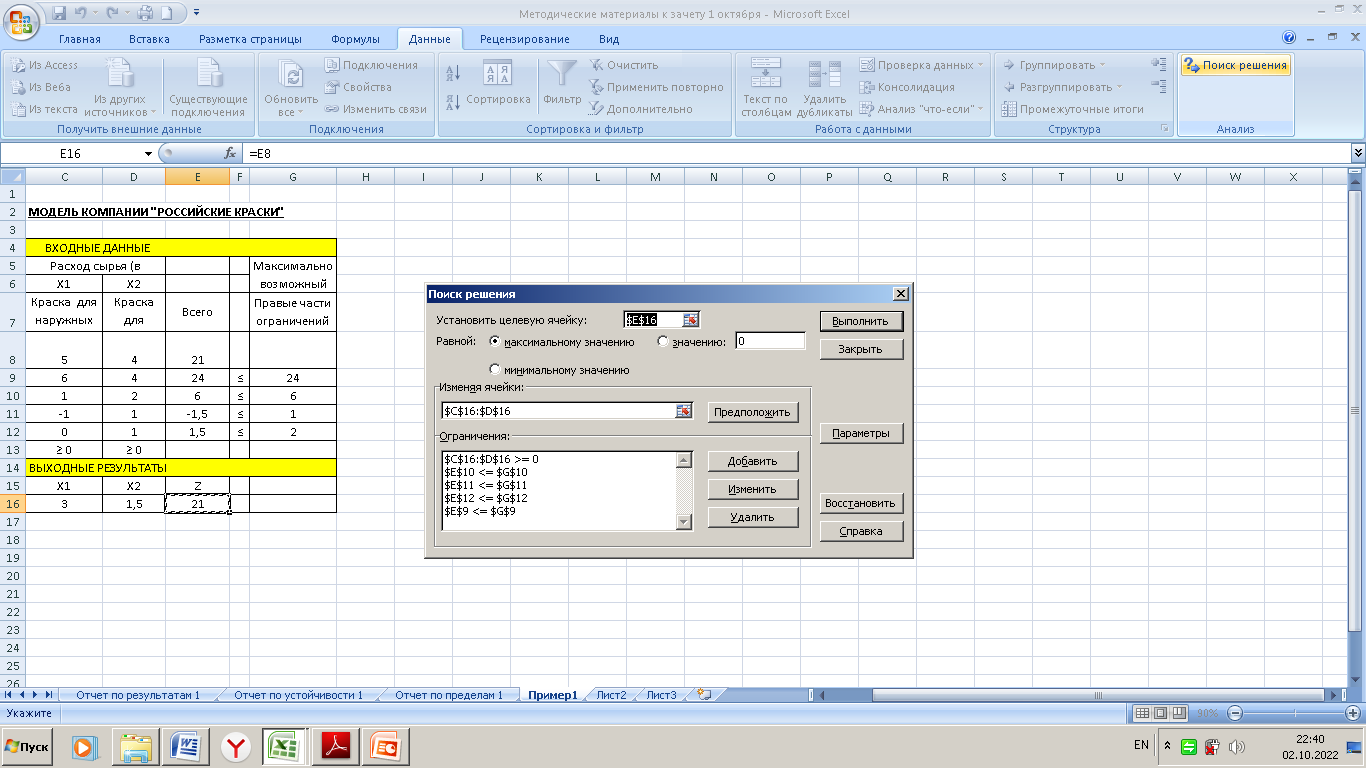
Поясняющие заголовки и надписи необходимы для того, чтобы сделать табличное представление модели более понятным и удобочитаемым. Относительное расположение ячеек, содержащих информацию разных типов, может быть другим. Покажем соответствие между математической и табличной моделями. Начнем с соответствия формул этих моделей. Коэффициенты целевой функции и левых частей ограничений помещены в диапазон ячеек С8:D12. После ввода исходных данных и расчетных формул табличная модель готова для использования средства Поиск решения. В меню Данные выберите команду Поиск решения. Откроется диалоговое окно «Поиск решения», показанное на рисунке 1.5.
Рисунок 1.5 – Диалоговое окно «Поиск решения» Рассмотрим опции окна Параметры поиска решения (рисунок 1.6).
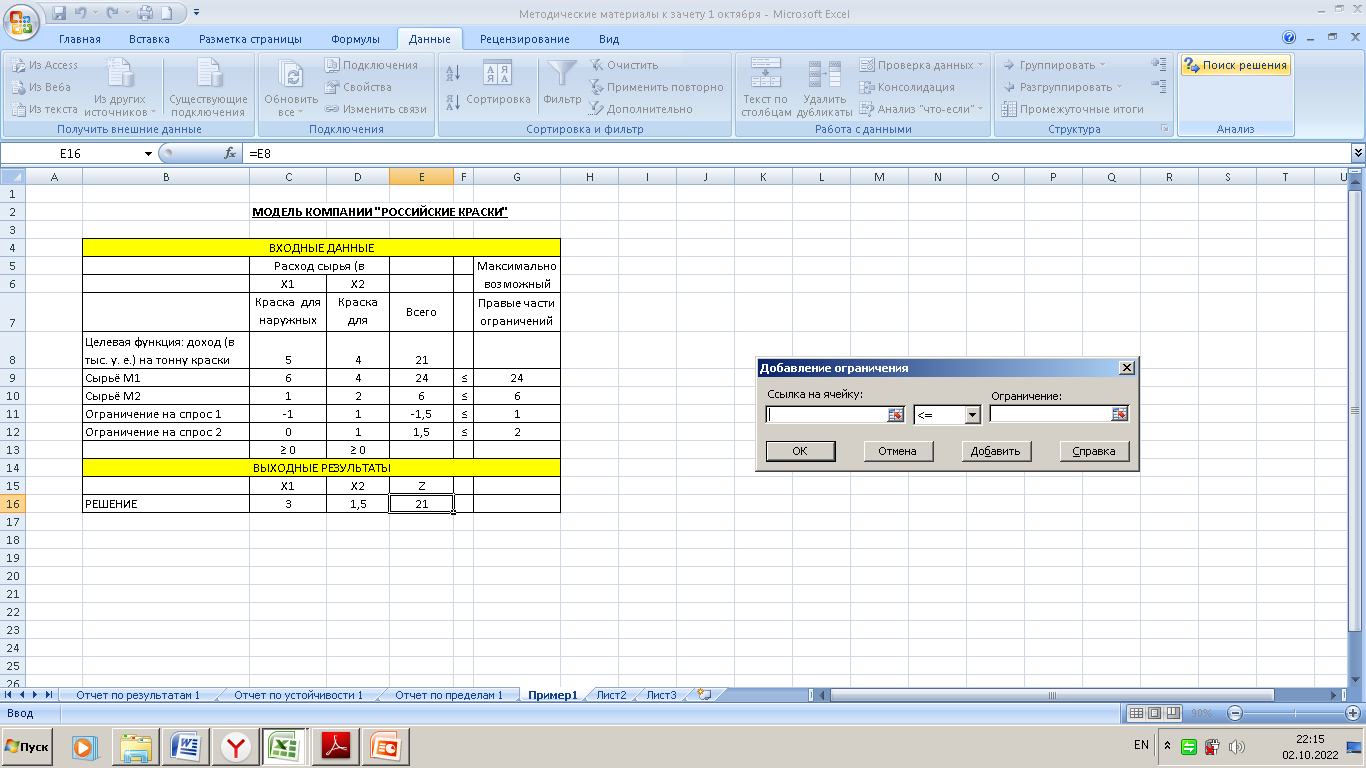
Оптимизировать целевую функцию. Указывается ячейка, содержащая целевую функцию (критерий оптимизации) рассматриваемой задачи. В нашей модели: $E$16. До. Следует выбрать из трех переключателей (Максимум, Минимум, Значения) тот, который определяет тип взаимосвязи между решением и целевой ячейкой. В нашей модели: Максимум. Изменяя ячейки переменных. Указываются ячейки, которые должны изменяться в процессе поиска решения задачи (ячейки, которые являются переменными задачи). В нашей модели: $C$16: $D$16. В соответствии с ограничениями. Отображаются ограничения, налагаемые на переменные задачи. Допускаются ограничения в виде равенств, неравенств, требования целочисленности переменных, принятия лишь двух значений – 0 или 1. Для добавления, изменения или удаления ограничения используются соответственно кнопки Добавить,_Изменить_или_Удалить.'>Добавить, Изменить или Удалить. Ограничения добавляются по одному за один раз и отображаются в окне Добавление ограничения (рисунок 1.7), вызываемом нажатием кнопки Добавить.
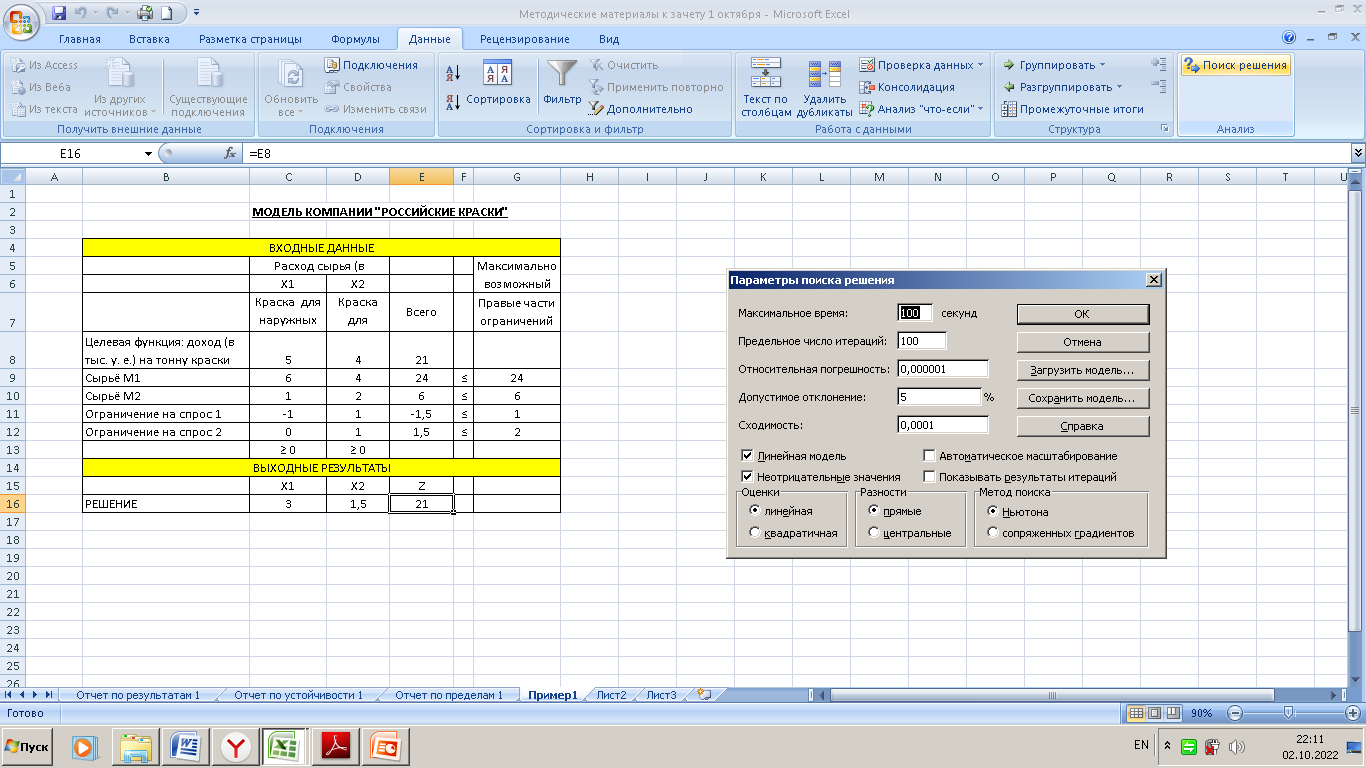
В поле Ссылка на ячейку вводится левая часть ограничений, в поле Ограничение — правая часть. Раскрывающийся список позволяет задать тип соотношения между левой и правой частями ограничения, а именно: >=, <=, =, цел, бин и разн. Соотношение цел подразумевает, что выражение может принимать только целочисленные значения, бин — только два значения (0 и 1), а разн — все значения должны быть различны. При нажатии кнопки Добавить в окно Добавление ограничения вводится вторая группа ограничений, налагаемых на переменные, а затем и последующие ограничения. Нажатие кнопки ОК завершает ввод ограничений. На экране опять отобразится окно Параметры поиска решения, но теперь уже заполненное. Используя это окно, вводим ограничения модели в таком виде $Е$9:$Е$12<=$G$9:$G$12. В ячейках G9:G12 записаны значения правых частей ограничений. Теперь осталось ввести ограничения неотрицательности для переменных. С помощью диалогового окна Добавление ограничения вводим $C$16:$D$16>=0 5. Сделать переменные без ограничений неотрицательными. Данный параметр устанавливает требование неотрицательности переменных задачи. Выберите метод решения. Позволяет выбрать метод (алгоритм оптимизации), который будет использоваться надстройкой Поиск решения для нахождения оптимального решения задачи. Из расположенного списка можно выбрать следующие методы: Поиск решения нелинейных задач методом ОПГ, Поиск решения линейных задач симплекс-методом и Эволюционный поиск решения. Внизу, под списком, приводится замечание по использованию указанных методов. Сбросить. Восстанавливает изначальные параметры Поиска решения, т. е. происходит сброс всех настроек окна Параметры поиска решения. Загрузить/сохранить. Сохранение (загрузка) различных данных для Поиска решения осуществляется с помощью кнопки окна Параметры поиска решения. Параметры. Позволяют изменять условия и варианты поиска решений исследуемой задачи (рисунок 1.7). Значения и состояния элементов управления, используемые по умолчанию, подходят для решения большинства задач. Найти решение. Запускает поиск решения при установленных параметрах. Но завершении работы на экране отобразится окно Результаты поиска решения. Рассмотрим опции окна Параметры [6]. 1. Вкладка Все методы. 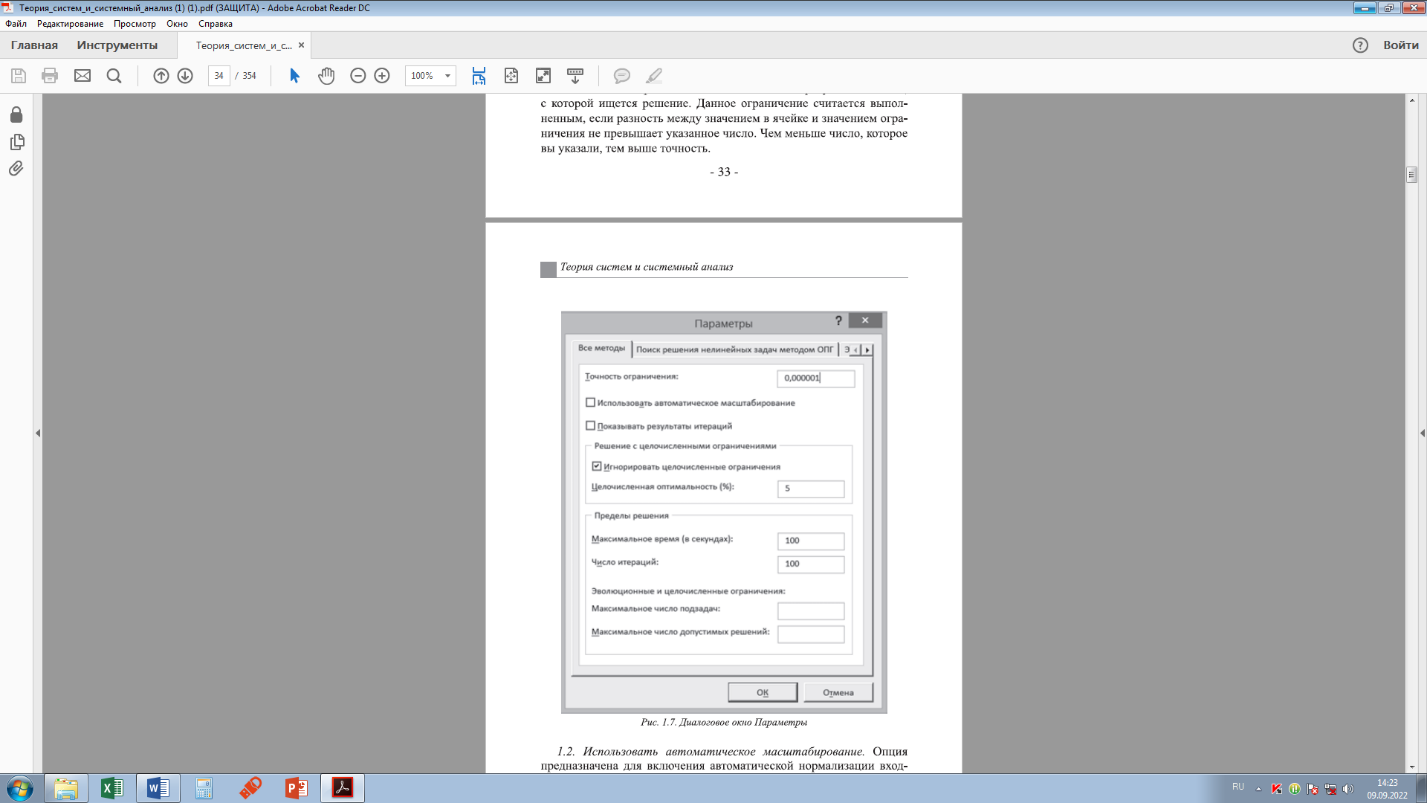 Рисунок 1.7 – Диалоговое окно Параметры Точность ограничения. Устанавливается требуемая точность, с которой ищется решение. Данное ограничение считается выполненным, если разность между значением в ячейке и значением ограничения не превышает указанное число. Чем меньше число, которое вы указали, тем выше точность. Использовать автоматическое масштабирование. Опция предназначена для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине. Показывать результаты итераций. Используется для приостановки поиска решений и просмотра отдельных итераций с целью получения дополнительной информации. Группа Решение с целочисленными ограничениями. Данная группа включает следующие параметры: Игнорировать целочисленные ограничения и Целочисленная оптимальность (%). Первый флажок устанавливается для задач с требованием целочисленности, бинарности и различных значений. Поиск решения определит паи лучшие значения с указанной точностью. Значение по умолчанию для параметра Целочисленная оптимальность (%) составляет 1 %. Установите значение 0 % для получения наиболее точного решения задачи с целочисленными или бинарными ограничениями. Группа Пределы решения. Максимальное время (в секундах) ограничивает время, отпускаемое на поиск решения задачи. Число итерации ограничивает число промежуточных вычислений. Эволюционные и целочисленные ограничения применяются только для задач, которые включают требования целочисленности переменных или используют эволюционный метод решения. Здесь два параметра: максимальное число подзадач – устанавливает максимальное число подзадач, которые вы хотите разрешить; максимальное число допустимых решений – устанавливает максимальное количество возможных решений, которые вы хотите разрешить; если возникают проблемы с целыми ограничения, то ото максимальное число целых допустимых решений. Вкладка Поиск решения нелинейных задач методом ОПГ. Сходимость. Устанавливается значение допустимого отклонения для оптимального решения, Группа Производные. Служит для выбора метода численного дифференцирования. при установке переключателя в положение Центральные при решении задачи используются более точные центральные разности, однако время вычислений значительно возрастает. Группа Несколько начальных точек. Данная группа используется для последовательного поиска оптимального решения. Установите флажок Использовать несколько начальных точек для того, чтобы процесс поиска решения обрабатывал несколько стартовых вариантов конкретной задачи. Размер совокупности – устанавливается количество вариантов решения, причем минимальный размер совокупности составляет 10, а максимальный – 200. Случайное начальное значение – выберите начальное положительное значение, которое будет использоваться генератором случайных чисел в качестве стартового значения при решении задачи оптимизации. Это ведет к поучению различных итоговых значений. Если это поле оставить пустым, то генератор случайных чисел будет при каждом новом шаге решения задачи генерировать произвольно число. Обязательные границы для переменных – задастся верхняя и нижняя границы для переменных при поиске оптимального решения. |