Линейное программирование. Подготовка к зачёту. часть 1.ЛП. 1. методы решения задач линейного программирования
 Скачать 1.44 Mb. Скачать 1.44 Mb.
|
|
3. Вкладка Эволюционным поиск решения. Сходимость. Устанавливается значение допустимого отклонения для оптимального решения. Скорость изменения. Число между 0 и 1, указывающее относительную частоту изменения в совокупности решений. Размер совокупности. Устанавливается количество вариантов решения, причем минимальный размер совокупности составляет 10, а максимальный — 200. Случайное начальное значение. Выберите начальное положительное значение, которое будет использоваться генератором случайных чисел в качестве стартового значения при решении задачи оптимизации. Максимальное время без улучшения. Вводится максимальное число секунд, допускающее поиск решения без существенного улучшения с использованием метода эволюционного поиска. Обязательные границы для переменных. При установке данного флажка эволюционный метод будет работать лишь тогда, когда вы определите верхнюю и нижнюю границы для переменных в списке ограничений. Для нахождения оптимального допустимого решения рассмотренной задачи линейного программирования необходимо щелкнуть на кнопке Выполнить в диалоговом окис Поиск решения. Решение появится в выходных ячейках В13:D13 табличной модели (рисунок 1.8) Оптимальное значение целевой функции появится в ячейке D5, а значения переменных х1 и х2 – в ячейках В13 и С13 соответственно. В ячейке D13 дублируются значения целевой функции, т, к. в эту ячейку введена формула =$D$5. 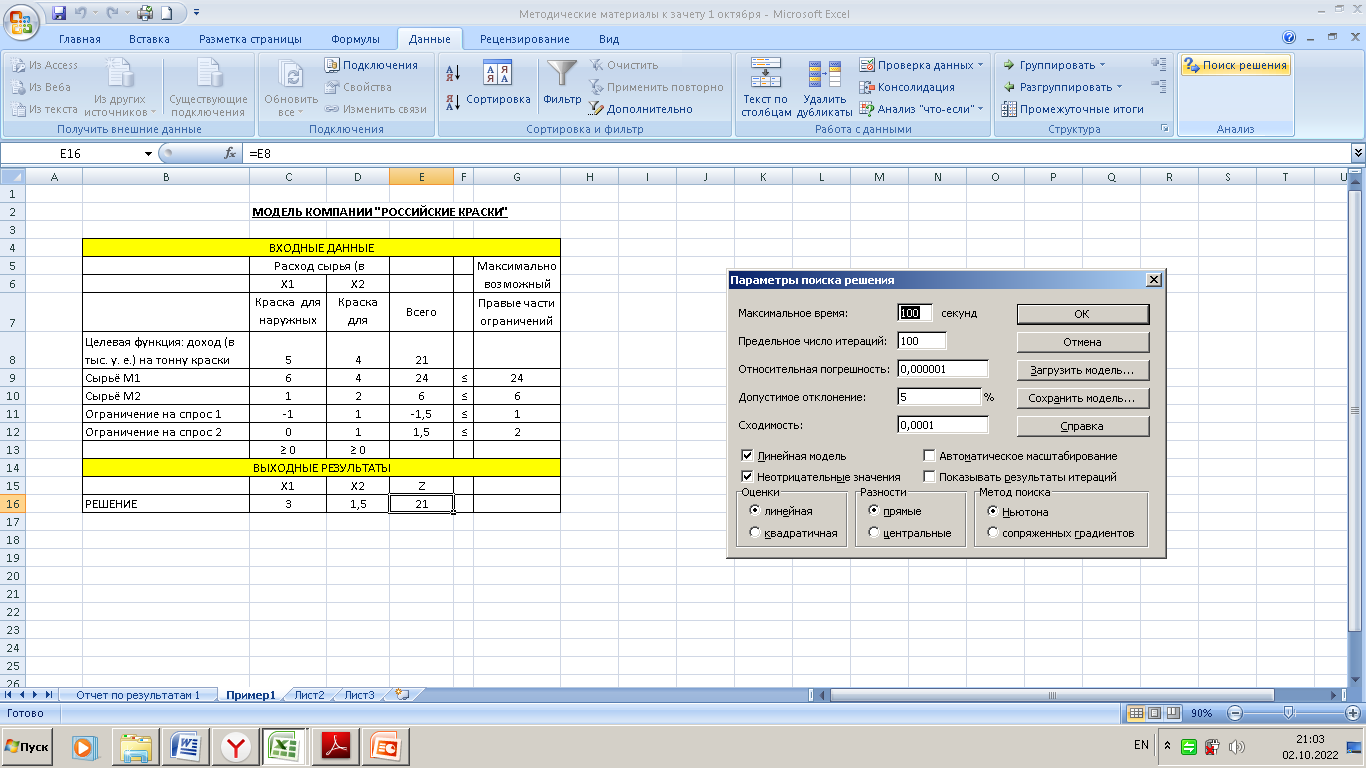 Рисунок 1.8 – Решение задачи в MS Excel Полученное оптимальное решение совпадает с результатом решения задачи линейного программирования геометрическим методом (рисунок 1.2) и результатом решения задачи линейного программирования симплексным методом (таблица 1.9). Также появится новое диалоговое окно Результаты поиска решения (рисунок 1.9), которое даст возможность получить более детальную информацию о решении в виде отчетов, которые формируются на отдельных листах рабочей книги (рисунки 1.10, 1.11, 1.12). 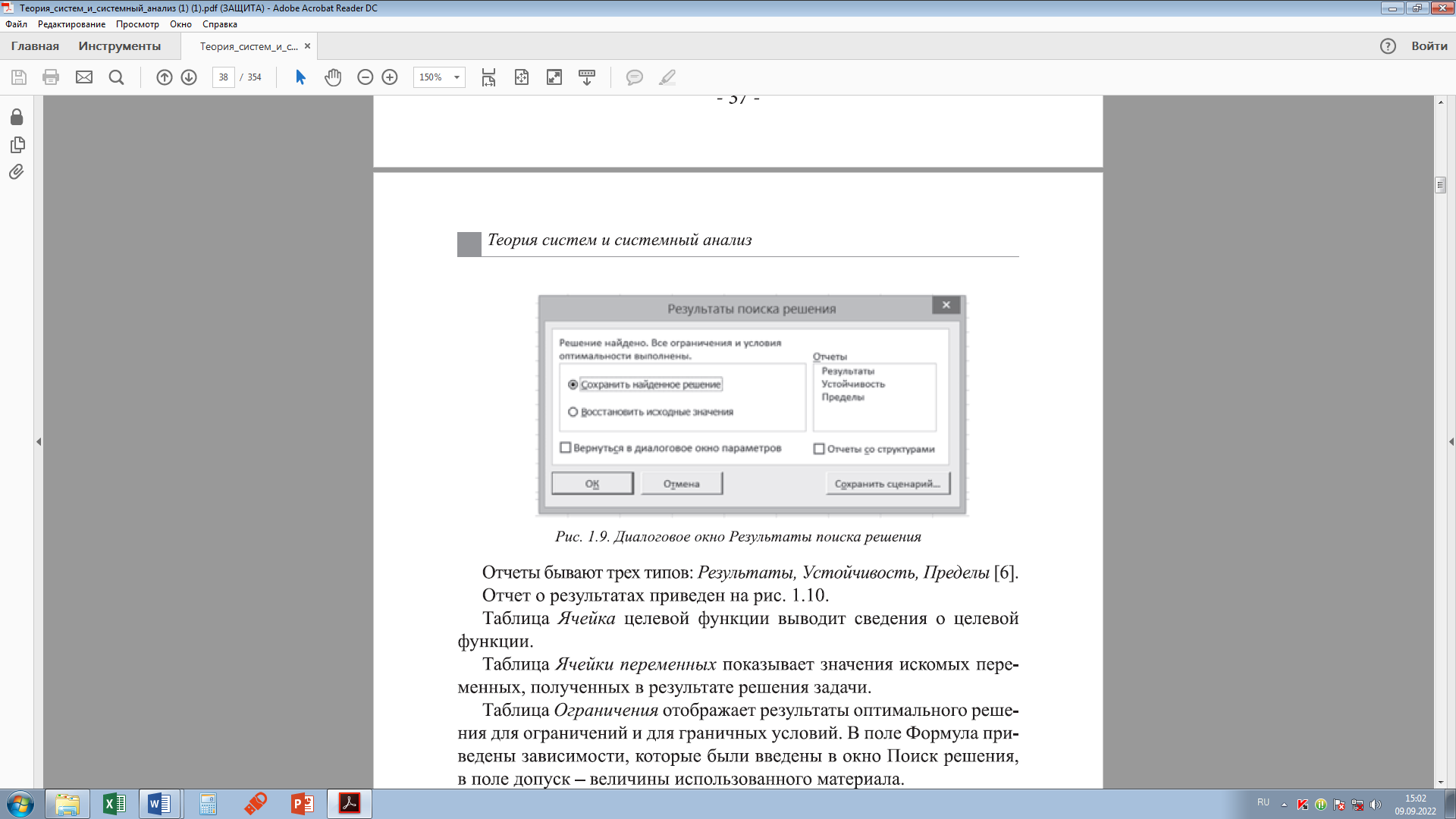 Рисунок 1.9 – Диалоговое окно Результаты поиска решения Отчеты бывают трех типов:Результаты, Устойчивость, Пределы. Отчет о результатах приведен на рисунке 1.10.
Рисунок 1.10 – Лист MS Excel с отчетом о результатах Таблица Ячейка целевой функции выводит сведения о целевой функции. Таблица Ячейки переменных показывает значения искомых переменных, полученных в результате решения задачи. Таблица Ограничения отображает результаты оптимального решения для ограничений и для граничных условий. В поле Формула приведены зависимости, которые были введены в окно Поиск решения, в поле допуск – величины использованного материала. Если материал используется полностью, то в поле Состояние указывается привязка, при неполном использовании материала в данном иоле указывается без привязки. Для граничных условий приводятся аналогичные величины с той лишь разницей, что вместо величины неиспользованного продукта показана разность между значением переменной в найденном оптимальном решении и заданным для нее граничным условием. Отчет об устойчивости приведен на рисунке 1.11. В таблице Ячейки переменных приводится результат решения задачи. В таблице Ограничения выводятся значения для ограничений, при которых сохраняется оптимальный набор переменных, входящих в оптимальное решение. Отчет о пределах приведен на рисунке 1.12. В отчете показано, в каких пределах может изменяться количество материалов, вошедших в оптимальное решение, при сохранении структуры оптимального решения: приводятся значения переменных в оптимальном решении, а также нижние и верхние пределы изменения значений переменных, здесь также указаны значения целевой функции при выпуске данного типа продукции на верхнем и нижнем пределах.
Рисунок 1.11 – Лист MS Excel с отчетом об устойчивости
Рисунок 1.12 – Лист MS Excel с отчетом о пределах 1.6 Использование среды Mathсad для решения задачи линейного программированияРезультат решения задачи об оптимальной производственной программе выпуска краски в среде Mathсad приведен на рисунках 1.13, 1,14 [3 Итог вычислений совпадает со всеми ранее полученными ответами. 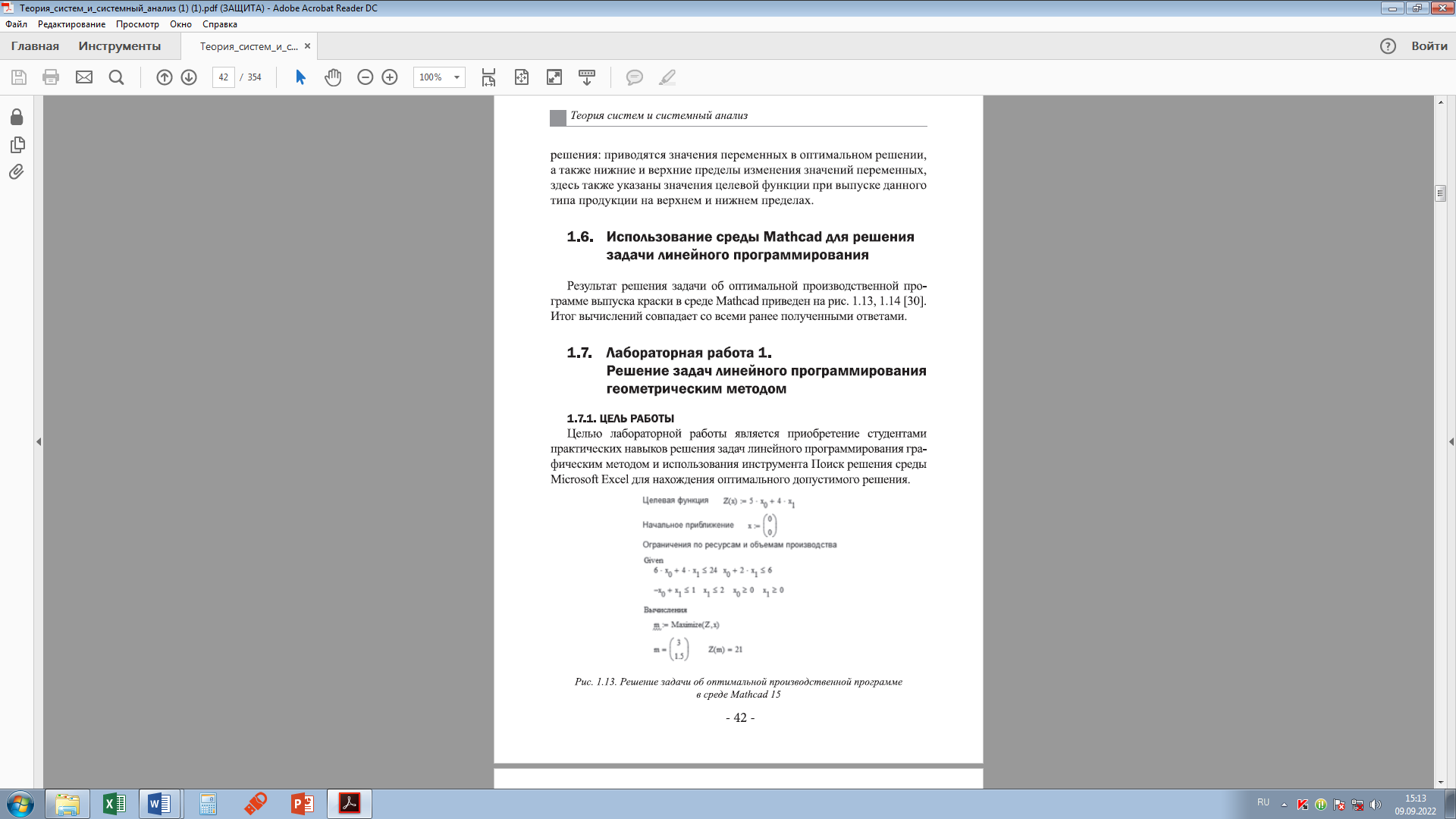 Рисунок 1.13 – Решение задачи об обязательной производственной программе в среде Mathcad 15 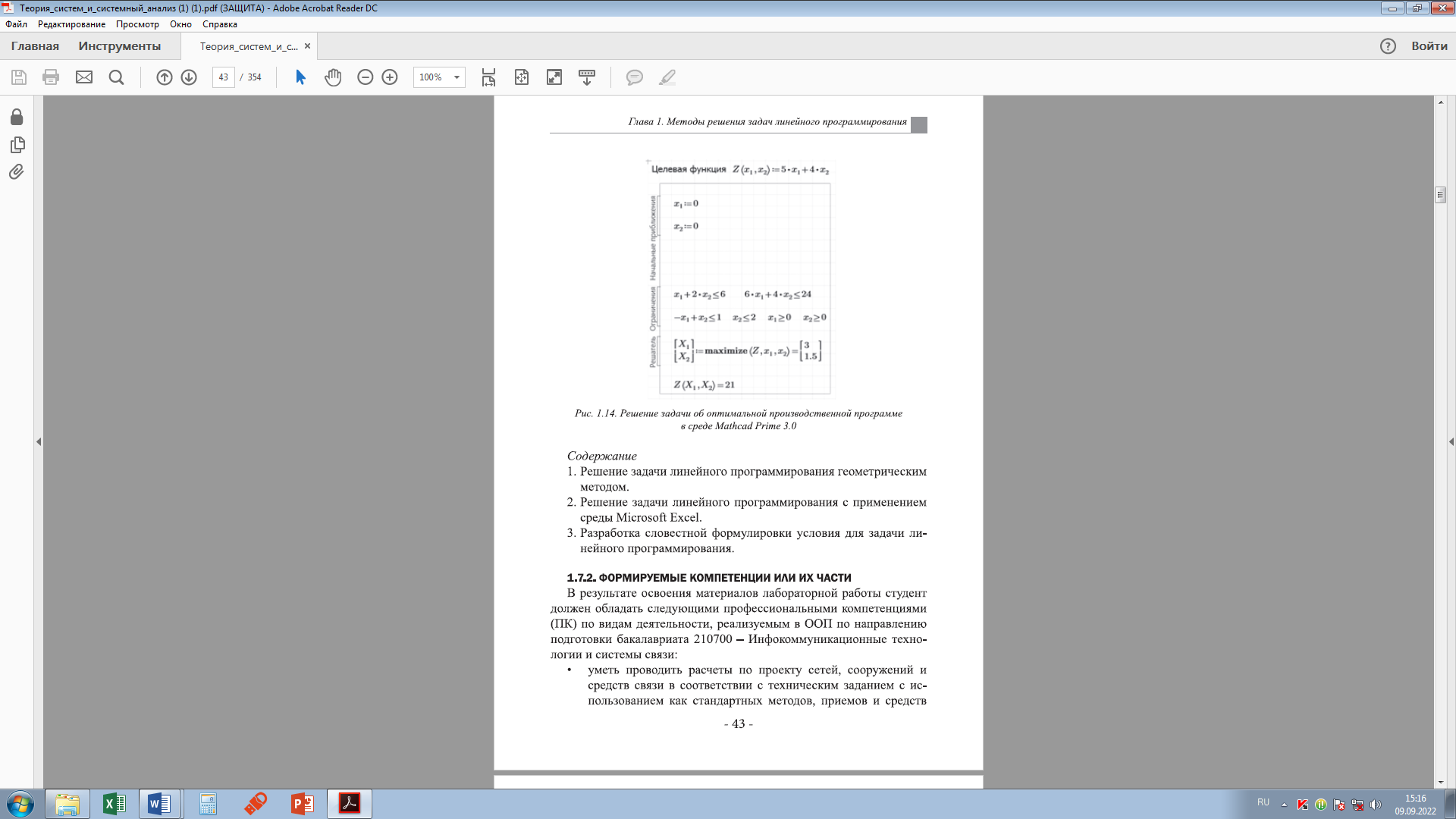 Рисунок 1.14 – Решение задачи об обязательной производственной программе в среде Mathcad Prime 3.0 ВОПРОСЫ К ЗАЧЁТУ Охарактеризуйте классификацию проблем, применяемую в системном анализе. Назовите 3 элемента задачи линейного программирования. Прокомментируйте этапы применения графического метола при решении задачи линейного программирования. Особенности использования табличного редактора MS Excel для решения задачи линейного программирования. Назовите основные черты, присущие процессам отыскания оптимальной стратегии управления. Какие шаги выполняются при использовании симплексных таблиц при решении задачи линейного программирования? Особенности выбора начальной точки расчетов в симплексном методе решения задачи линейного программирования. Особенности применения Mathcad для решения задач линейного программирования, Список литературы Гарнаев А. Ю., Рудикова Л. В. Microsoft Office Excel 2010: разработка приложений. — СПб.: БХВ-Петербурт, 2011. Охорзин В. А. Прикладная математика в системе MATHCAD : учебное пособие. 2-е изд., испр. и доп.-СПб,: Лань, 2009. Таха X. А. Введение в исследование операций. — М.: Вильямс, 2007. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
